例の手遊び

本記事で取り扱う「例の手遊び」は、交互に指の本数を増やしていくアレのことです。

ヴォルデモート卿やペニーワイズみたいな呼び方をしているのはなんでかというと、私の文化圏ではそれに名前が与えられていなかったからです。
地域によっては「マッチ棒」「割り箸」「電信棒」などと呼ぶらしいですね。闇の帝王が雑貨に成り下がってしましました。^[1]

ゲームの基本的なルールは手を用いた遊び - Wikipediaを参照してください。

解析しよう

やること

やることは次の2つです。

• 勝利が確定するパターンをすべて求めて、流れをグラフ^[2]として可視化する。
• 千日手が存在するならば、千日手をすべて求めてグラフとして可視化する。

考え方

「双方のプレイヤーの指の本数」と「そのターンに行動できるプレイヤー」をまとめてゲームの「状態」として、全ての状態について調べるというのが基本の考え方です。

指の本数が0~4本のルールについて考えてみると、状態数は多くても$4^4\times 2=512$個であり、余裕で全ての状態について調べられそうなことがわかります。左右の手の区別をなくせばさらに状態数が減りそうです。

つぎに「勝利が確定」とは何かということを考えます。
とりあえず「先手の勝利が確定する状態」とはどのような状態であるかを考えてみましょうか。

先手の勝利が確定する状態とは……
それ以降後手がどのような操作をしても……先手が適切に操作することによって……有限回？のターンで先手が勝利することができる状態……？？？

よくわかりません。数式を全く使わず物事を考えるのはたいへん難しい^[3]ので、まず例のゲーム自体を雑に定式化^[4]してしまいましょう。

ゲームは、5つ組$G=(S,p,T,w,s_0)$で与えられる。ここで

1. $S$は初期状態から到達可能な全ての状態の有限集合である。
2. $p$はプレイヤー関数$S\to \{\text{先手},\text{後手}\}$であり、この関数は状態が与えられたときに、その状態を遷移させることができるプレイヤーを与えるものである。
3. $T$は状態遷移関数$S\to 2^S$^[5]であり、この関数は状態が与えられたときに、次に遷移することができる状態の集合を与えるものである。
4. $w$は勝者関数$S\to \{先手,後手,ゲーム継続\}$であり、この関数は状態が与えられたときに、その状態に至ることで片方のプレイヤーが勝利するならば勝者のプレイヤーを、そうでなければゲーム継続を与えるものである。
5. $s_0\in S$はゲームの初期状態である。

できました。オートマトンっぽくてかわいいですね！これで$(S,p,T,w,s_0)$を適切に設定することで、例の手遊びを表現することができます。

いま求めたいのは、先手の勝利が確定する状態全てからなる集合$W_{\text{先手}}$です。ここで、次のことがいえます。

1. 任意の$s\in S$について、$w(s)=\text{先手}$ならば、明らかに$s\in$$W_{\text{先手}}$である。
2. 任意の$s\in S$について、$p(s)=\text{先手}$かつ、ある$t\in T(s)$が存在して$t\in W_{\text{先手}}$ならば、先手が$s$から$t$に状態を遷移させることで先手の勝利が確定するから、$s\in W_{\text{先手}}$である。
3. 任意の$s\in S$について、$p(s)=\text{後手}$かつ、すべての$t\in T(s)$について$t\in W_{\text{先手}}$ならば、後手は先手の勝利が確定する状態に遷移させるしかないので、$s\in W_{\text{先手}}$である。

逆に、1番をもとにして2, 3番を根拠に$W_{\text{先手}}$に含まれる状態の集合$W$を広げていけば、最終的に$W=W_{\text{先手}}$となり$W_{\text{先手}}$が求められそうな気がします^[6]。考え方はミニマックス法に非常に近いです。これを擬似コードにすると以下のようになります。

1. $W\leftarrow \{s\in S\mid w(s)=\text{先手}\}$
2. $p(s)=\text{先手}$かつ、ある$t\in T(s)$が存在して$t\in W$
   または
   $p(s)=\text{後手}$かつ、すべての$t\in T(s)$について$t\in W$
   を満たす$s\in S\setminus W$^[7]が存在する限り、$W\leftarrow W\cup \{s\}$を繰り返す
3. $W$が求める$W_{\text{先手}}$である。

$W_{\text{後手}}$も同様にして求めることができそうです。
また、$S$からこれらを除外した状態の集合$S\setminus (W_{\text{先手}}\cup W_{\text{後手}})$に含まれる状態では、双方のプレイヤーが最前を尽くした場合にゲームが終了しないことがわかります。千日手です。

実践

勝利が確定するような状態の求め方がわかりましたが、状態を列挙して文字を吐き出すだけだとあまり面白くありません。ここはどうにかして可視化したいです。

そのためにgraphvizというツールを使いました。
graphvizはDOT言語というグラフを記述する言語を画像化してくれるすごいやつで、つまるところ

digraph {
  a [label="first\nf{1, 1}\ns{1, 1}"]
  b [label="second\nf{1, 1}\ns{1, 2}"]
  c [label="second\nf{1, 2}\ns{1, 1}"]
  d [label="second\nf{0, 2}\ns{1, 1}"]
  a -> b
  a -> c
  a -> d
}

↑これが

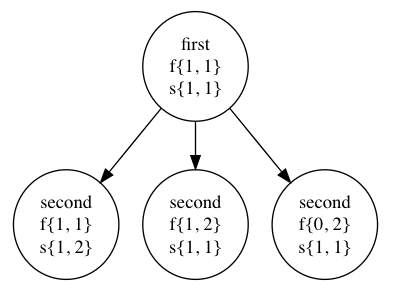
↑こうなります。

このように、グラフのノード(頂点)をゲームの状態、矢印を状態遷移としてゲームの流れを可視化してしまいましょう。
ゲームを解析してDOT言語として出力するプログラムを書きました。
https://github.com/roodni/finger-game-solver

ついに記事の目標が達成されます。手始めに、私の文化圏で最も流通していたmod5、分身結合が常に可能、自分への攻撃も可能ルールにおける先手の勝ちパターンを可視化しましょう。

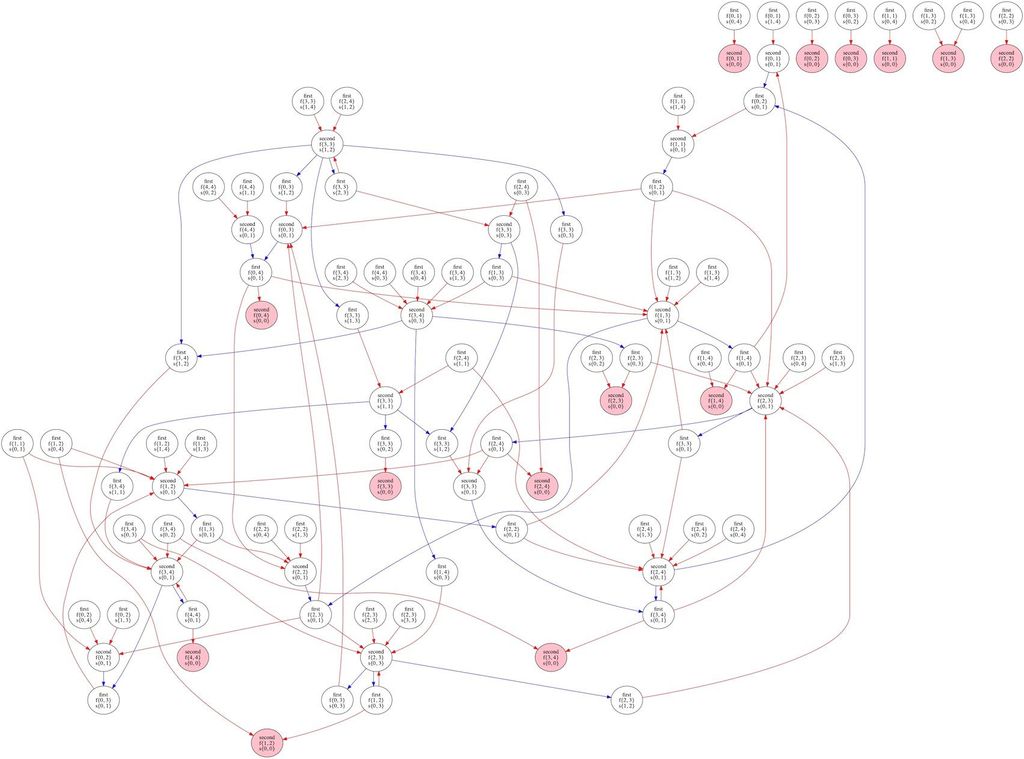
素晴らしい！！！私が小中学生のとき探し求めた勝利法の全てが解き明かされたわけです。
グラフの読み方ですが、赤色の矢印が先手プレイヤーの選択で、青色の矢印が後手プレイヤーの選択です。また、赤色に塗りつぶされたノードは先手の勝利状態($w(s)=\text{先手}$となること)を示しています。
グラフを読んでいると「自分が{3,3}で相手が{1,4}のときに勝利確定」など意外と発見があります。感動的ですね。また、グラフに初期状態が含まれていないので、このゲームは先手必勝ではないということもわかります。

次は千日手の可視化です。これで私はこの手遊びの全てを理解……

なんだこれは。読めたものではありません。
仕方がないので初期状態から千日手の流れを幅優先探索して、既出の状態を灰色の輪郭で示し探索を打ち切るようにグラフの作りを変えてみます。

今度はやたら横に長くなってしまいました……こちらは拡大すれば読めるのですが、ブログに写真を貼るのは難しそうです。興味のある方はプログラムを実行する^[8]か、解析プログラムを自作するかしてみてください。

面白かったグラフをいくつか紹介します。

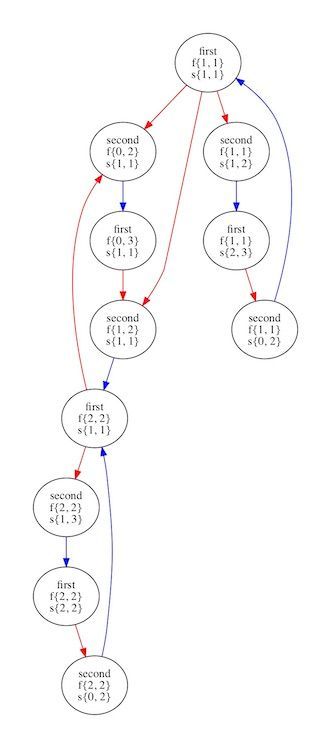
↑これは指を1本減らしたmod4ルールにおける千日手のグラフです。相手が勝ちパターンをすべて把握していれば、当然このグラフから外れた瞬間に負けが確定します。
指を一本減らすだけでゲームの規模が極端に小さくなってしまうのです。mod5ルールがよくできていることがわかります。

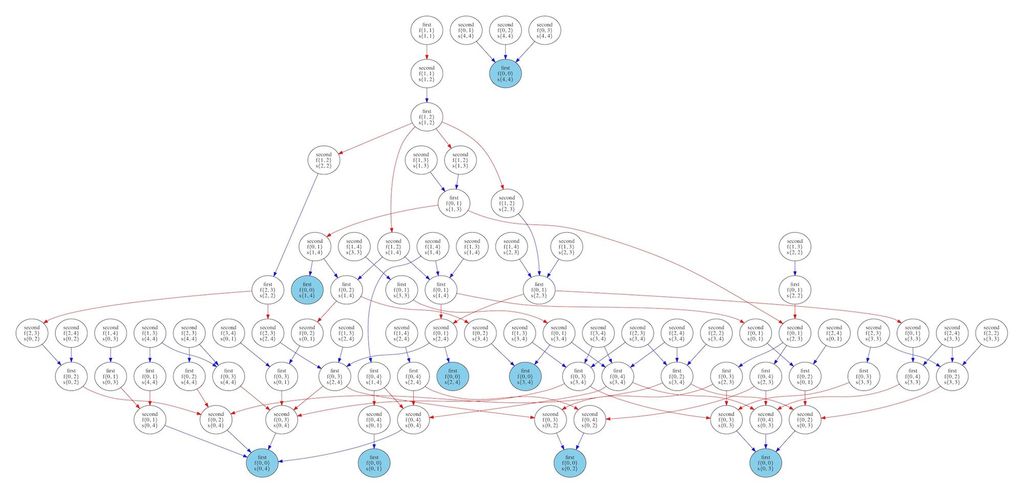
↑これは自分への攻撃および分身を禁止し、さらに指本数が5以上になったらその手は消滅というルールにおける後手の勝ちパターンです。初期状態が含まれているので、このルールでは後手が必勝であることがわかります。
調べてみると、分身、自分への攻撃、mod5がどれか一つでも可能なルールでは必勝法が存在しないということがわかります。このゲームが先手必勝または後手必勝となるのはルールが非常に厳しいときに限られるということです。

おわり

おわりです。ありがとうございました。
本当はコンピュータと対戦できるブラウザゲームを作って公開したかったんですが、2日前までゲーム制作を放置していたので間に合いませんでした。愚かですね。^[9]
あるいは、ゲームを作り慣れていれば間に合わせることができたのかもしれません……^[10]

明日はtarorynさんとEruさんの記事です。お楽しみに！