一変数多項式の解を近似で求める求根アルゴリズムについて(9.5割Newton法です)
※数学的記述はおきもちであって正確でない場合があります(指摘お待ちしております)
Newton法(Newton-Raphson法)
目標
一変数実多項式(の係数)が与えられたときに、が十分小さいを求める
概要
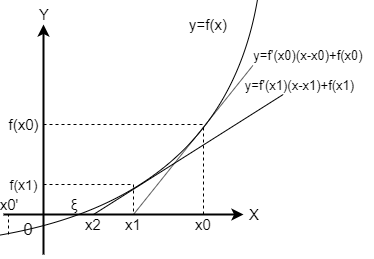
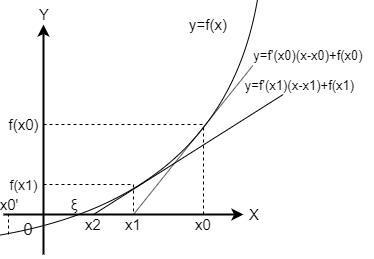
とを方程式の解に対する近似値とし、この方程式が区間に唯一の解を持つとします。を、座標におけるの接線と座標の交点とします。このときは
なので、一般に以上の整数に対して
であることが分かります。グラフを見ると、これを繰り返していけば目標が達成できそうです。
誤差の評価
実際に誤差がどのような振る舞いをするのか気になるので、具体的にみるためにをまわりでTaylor展開することを考えます。
はを含む開区間で級なのでこの展開は可能で、次まで展開すると、
これにを代入すると、
変形して、
いま、
であるから(∵)、つ前の式を代入すれば
よって、誤差は前の誤差の乗に比例して小さくなることが分かります(二次収束)。
つまり、が増える毎に正確な桁数がだいたい倍になるということです←すごい
※注意※
グラフを見ると、ではなくから始めた場合は解の近似は得られません。また、の場合にもが求まりません。適用できるのは、
「とが区間でとならず、との符号が異なり、とが同符号である端点から始める場合」です。このときに含まれる唯一の解の近似が求まります。(力不足により証明略)
使用例
- の近似
これはを解く事と同じなので、これについてNewton法を適用します
とすればより初期値を適当な大きい数にすれば適用できる条件を満たせます
C++での実装例:
double newton_sqrt(double x,double eps=1e-8){
if(x < 0)return -1;
if(!x)return 0;
double res = x < 1 ? 1 : x; //初期値
while(res*res - x > eps){
res = res - (res*res - x) / (2*res);
}
return res;
}
mt19997で回実行したら1700msかかりました 尚 std::sqrt 17ms …
- の近似
さっきみたいにを解きます、の符号はの符号と必ず同じなのでなら十分小さい負数を、なら十分大きい正数を初期値にします
C++での実装例:
double newton_cbrt(double x,double eps=1e-8){
if(!x)return 0;
double res = abs(x) < 1 ? (x < 0 ? -1 : 1) : x ; //初期値
while(abs(res*res*res - x) > eps){
res = res - (res*res*res - x) / (3*res*res);
}
return res;
}
mt19997で実行すると2670ms ( std::cbrt 750ms STLすごい)
- とかとか三角関数の近似
Taylor展開である程度の次数まで展開してやれば、これらも有限次数の多項式で表せるので、Newton法が使えます
DKA法(Durand-Kerner-Aberth法)
Newton法を改良し、複素数の解も含んだ一般の代数方程式にも適用できるようにしたもの
謝罪
DKA法を読んでください(丸投げ)
まとめ
- Newton法は実多項式の近似解を素早く求められる(例外アリ)
- Newton法とTaylor展開で色んな初等関数の求根もできる
- DKA法はすごい
- Wolfram Alpha は最高