電気力線をプロットしてみた【AdC2019 27日目】

ちょうど電磁気学の勉強をしているときにこんな問題を見つけました。

単位長さ当たり $λ_{1}, λ_{2}, λ_{3}, \dots λ_{n}$ に帯電した無限長のn本の直線電荷があるときの電気力線の方程式を求めよ。ただし、各直線と電気力線上の点とを結ぶ直線が一定方向となす角をそれぞれ $θ_{1}, θ_{2}, θ_{3}, \dots, θ_{n}$ とする。

答えは↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓

答え

$\sum_{i = 1}^{n} λ_{i} θ_{i} =$ 一定

皆さん解けましたか。僕は速攻で答えを見たのですが、この式を見ても全然ピンと来なかったです。

解説

一応解説を書いておきます。直線電荷を真上から見た図で考えます。

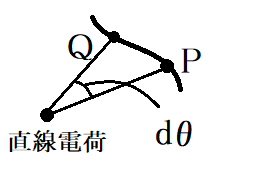
まず、↑図のように適当な曲線PQ、なす角を $d θ$ とします。
線密度 $λ$ の直線電荷が出す電気力線の数は単位長さ当たり $\frac{λ}{ϵ _{0}}$ なので、曲線PQを通る電気力線の本数は
$\frac{λ θ}{2 π ϵ _{0}}$ 本です。n本の直線電荷があるときは、
$\sum_{i = 1}^{n} \frac{λ _{i} d θ _{i}}{2 π ϵ _{0}}$ 。ここで、電気力線同士は交わることがないので、曲線PQが電気力線となるのは $\sum_{i = 1}^{n} \frac{λ _{i} d θ _{i}}{2 π ϵ _{0}} = 0$ 。積分して $\sum_{i = 1}^{n} \frac{λ _{i} θ _{i}}{2 π ϵ _{0}} =$ 定数　が電気力線の方程式です。

以上が解説ですが、解説を読んでもいまいち納得できなかったです。というわけで、本当に電気力線になるのかプロットして確かめてみましょう。

プロット結果

完成するのに思ってたよりめちゃめちゃ時間がかかりましたが、なんとかできました。（本当に正しくコーディングできてるのかわからないけどそれっぽいので多分あってる？）。

2-3 3-1

プログラミング

ちょうど僕が参加しているプロジェクトの方でpixi.jsを使っていたので、それを使うことにしました。
とりあえずプログラムを置いておきます。実行するにはtypescriptでpixi.jsを使える環境を整えてください。

ココをクリックするとソースコードが出てきます

実行すると左クリックで電荷（真上から見た直線電荷）を置けます。Shiftを押しながらだと負電荷になります。BackSpaceで最近の電荷を消します。最大で8個の電荷を置けます。背景の画像用にbackground.pngを用意してください（用意しなくても動きます）。

main.tsimport * as PIXI from 'pixi.js'

const app = new PIXI.Application();
document.body.appendChild(app.view);
let shiftFlag: boolean = false;
let num = 0;
let filter: PIXI.Filter;

document.addEventListener('keydown',(event)=>{
    shiftFlag = event.shiftKey;
    if(event.keyCode === 8){
        num += 7;
        setNewCharge(0);
    }
})
document.addEventListener('keyup',(event)=>{
    shiftFlag = event.shiftKey;
})

function setNewCharge(q: number){
    var mouse = app.renderer.plugins.interaction.mouse.global;
    filter.uniforms.x[num % 8] = mouse.x;
    filter.uniforms.y[num % 8] = mouse.y;
    filter.uniforms.q[num % 8] = q;
}

const background = PIXI.Sprite.from('background.png');
background.width = app.screen.width;
background.height = app.screen.height;
app.stage.addChild(background);

background.interactive = true;
background.buttonMode = true;
background.on('pointerdown', () => {
    setNewCharge(shiftFlag ? -1 : 1);
    num++;
});

const shaderFrag = `
precision highp float;

varying vec2 vTextureCoord;

uniform vec2 mouse;
uniform vec4 inputSize;
uniform vec4 outputFrame;
uniform float x[8], y[8], q[8];

void main() {
    const float PI = 3.1415926535897932384626433832795;
    const float k = 30.0;//本数
    vec2 scr = vTextureCoord * inputSize.xy + outputFrame.xy;
    float sum = 0.0;
    for(int i = 0; i < 8; i++)
        sum += q[i] * atan(scr.x - x[i], scr.y - y[i]);
    float v = fract(sum * k / 2.0 / PI);
    v = min(v, 1.0 - v) * 2.0;
    gl_FragColor = vec4(pow(v, 4.0), 0.0, 0.0, 0.5);
}
`;
const container = new PIXI.Container();
container.filterArea = new PIXI.Rectangle(0, 0, app.screen.width, app.screen.height);
app.stage.addChild(container);

try{
     filter = new PIXI.Filter(null, shaderFrag, {
        mouse: new PIXI.Point(),
        x: [0,0,0,0,0,0,0,0],
        y: [0,0,0,0,0,0,0,0],
        q: [0,0,0,0,0,0,0,0]
    });
    container.filters = [filter];
}
catch{
    alert("GLSLのコードにエラーがあります。")
}

GLSLで書いてあるのはconst shaderFrag = から`で囲まれたところです。

GLSLではuniformとついた変数が、自由にユーザーが変更できる変数みたいです。電荷のデータは全てuniform変数で保管してます。
pos[0～7]が電荷の位置で、q[0～7]が各電荷の強さです。

今回は電気力線を描きたいのでSUM = $\sum_{i = 1}^{n} λ_{i} θ_{i}$ (以下SUMで表す)という値を周期的に0から1までの値(色の各成分は0から1の実数で表現されるから)を行ったり来たりするように変換することを考えます。
まずfract関数(引数の値の少数点以下の値を返却してくれる)を使います。
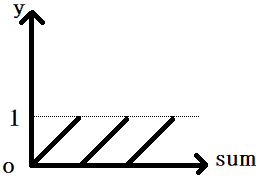
graph1
しかし、これでは1のすぐ次に0をとってしまいます（これはこれできれいな電気力線になるのですが）。
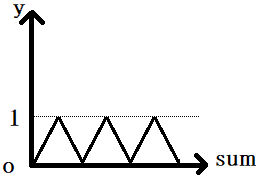
そこでfract関数でとった値をvとして、2.0 * min(v, 1.0 -v)として連続関数にします。
graph2
あとは線の太さを少し細目にしたいので、先ほどの値を2乗、あるいは3乗してあげて、
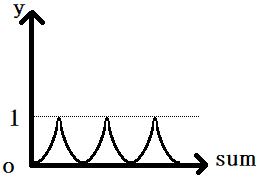
graph3
こんなイメージです。
こうしてできた数値をgl_FragColorに代入して、色の出力ができます。