こんにちは、@d_etteiu8383(でっていう)です。この記事はtraP新歓ブログリレー2021 13日目の記事です。

突然ですがここに立方体を用意しました。環境によっては正常に表示されない場合がありますが、マウスや指でぐりぐり動かすことができます。

いっぱいぐりぐりしていっぱい眺めてみると、いろんなことに気が付くと思います。
例えばこれ↓

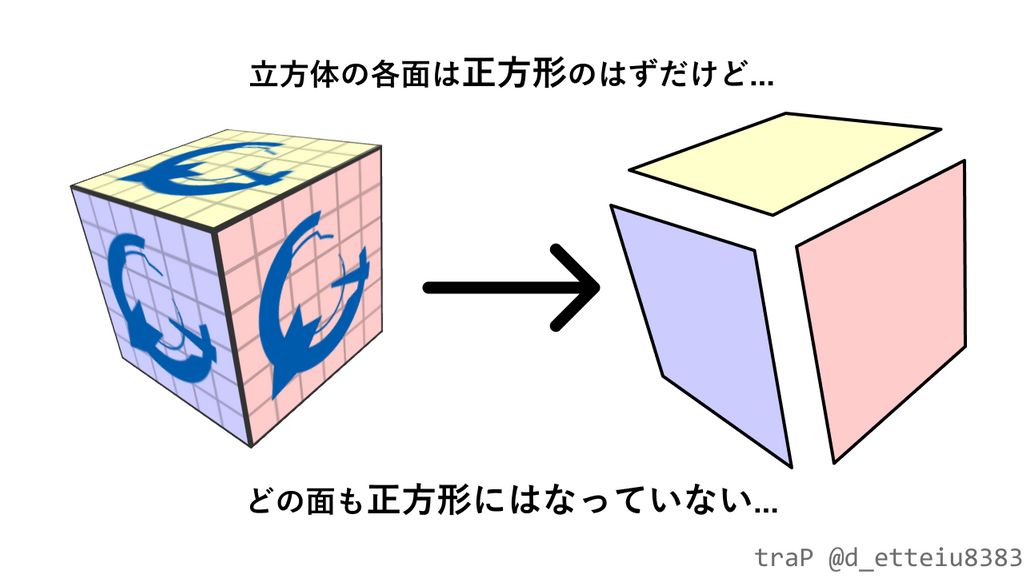
僕は上で「立方体を用意した」と説明しましたが、画像に示したように(そしてあなたがぐりぐりしているとき)各面は明らかに正方形になっていません。平行四辺形ですらありませんね。しかし立方体は6枚の正方形で構成されている図形のはずです。僕が嘘をついていて、本当は立方体ではなかった…?でも多くの方は上の図形をぐりぐりしながら「立方体だなぁ」と感じていたはずです。なぜ我々は歪な四角形の集合を「立方体だ」と認めたのでしょうか?なぜ我々は歪んだ四角形を「正方形だ」と感じたのでしょうか?「当たり前だろ」と思う方もいるとは思いますが、なぜこうなるのか理由を答えられる方は多くはないでしょう。

この記事では、空間中の正方形が歪んで見える理由の解説をしたいと思います。

"見る"ってなんだ

まず"見る"という行為について考えてみましょう。我々人間は目を通して、空間上の物体から発せられた光や物体表面で反射した光を、面状に配置された網膜で感受することにより"見る"を達成しています。空間上から届く光を平面状のフィルムで感受するカメラと同じですね。この光の経路を、移動経路と置き換えて考えてみましょう。
すると、"見る"という行為は"一定の移動手段のもとで3次元空間(つまり空間)上の点を2次元空間(つまり平面)上に移す操作"と言うことができそうです。

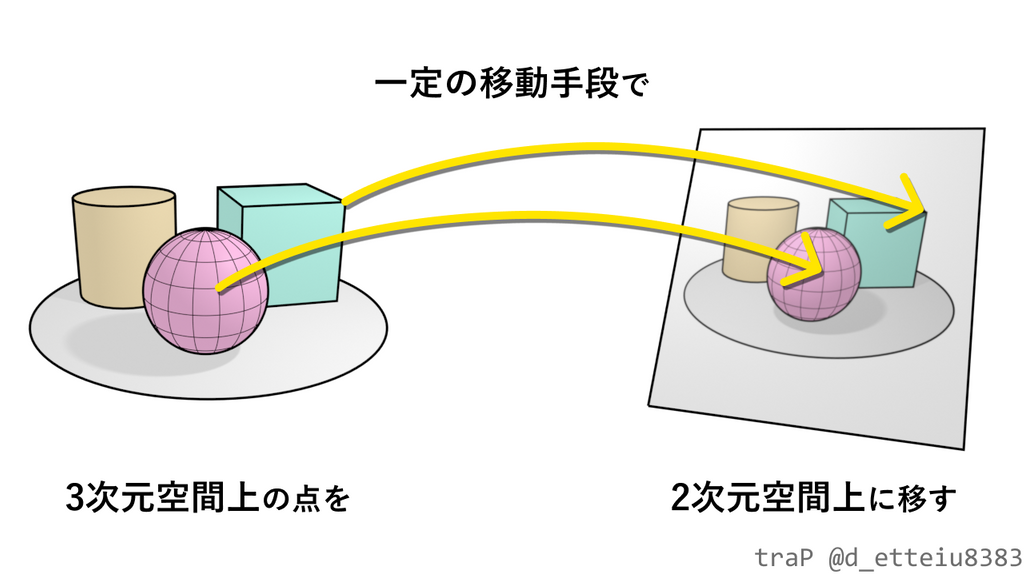
この"一定の移動手段"がどのような物かを解明すれば、正方形が歪んで見える理由もわかりそうです。しかし、空間から発せられた光が網膜に届くまでの経路を厳密に考えるのは少し面倒くさそうなので今回はもっと簡単なモデルで考えてみます。下図のようなモデルをイメージしてみてください。

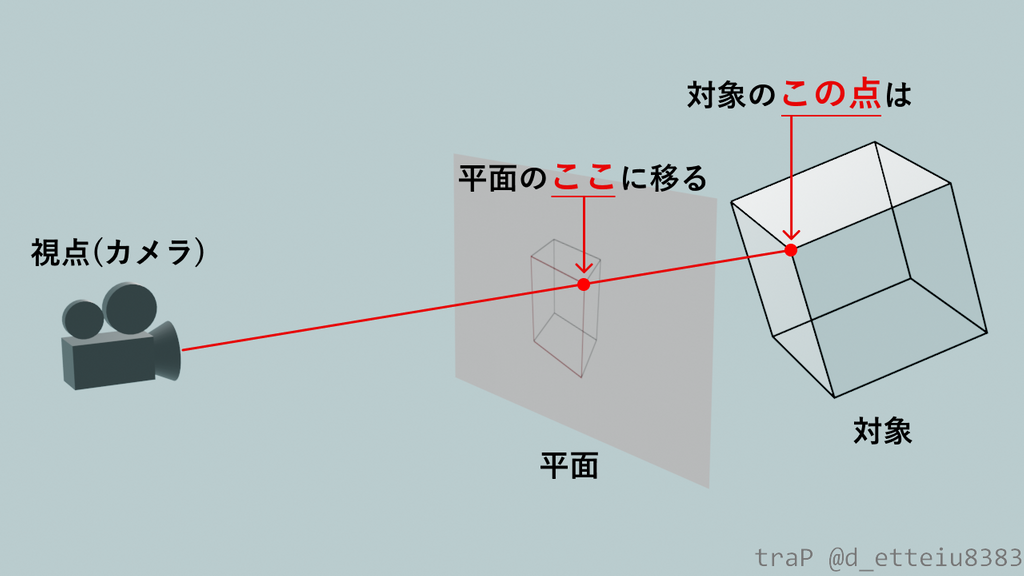
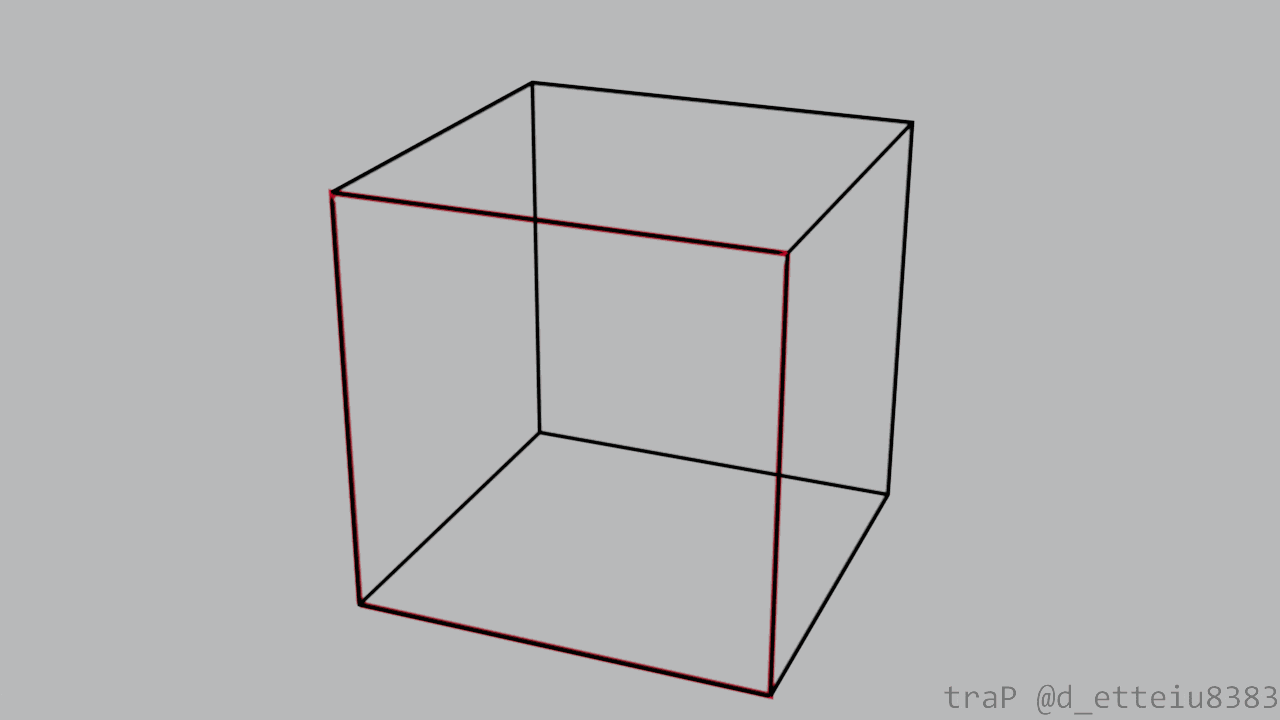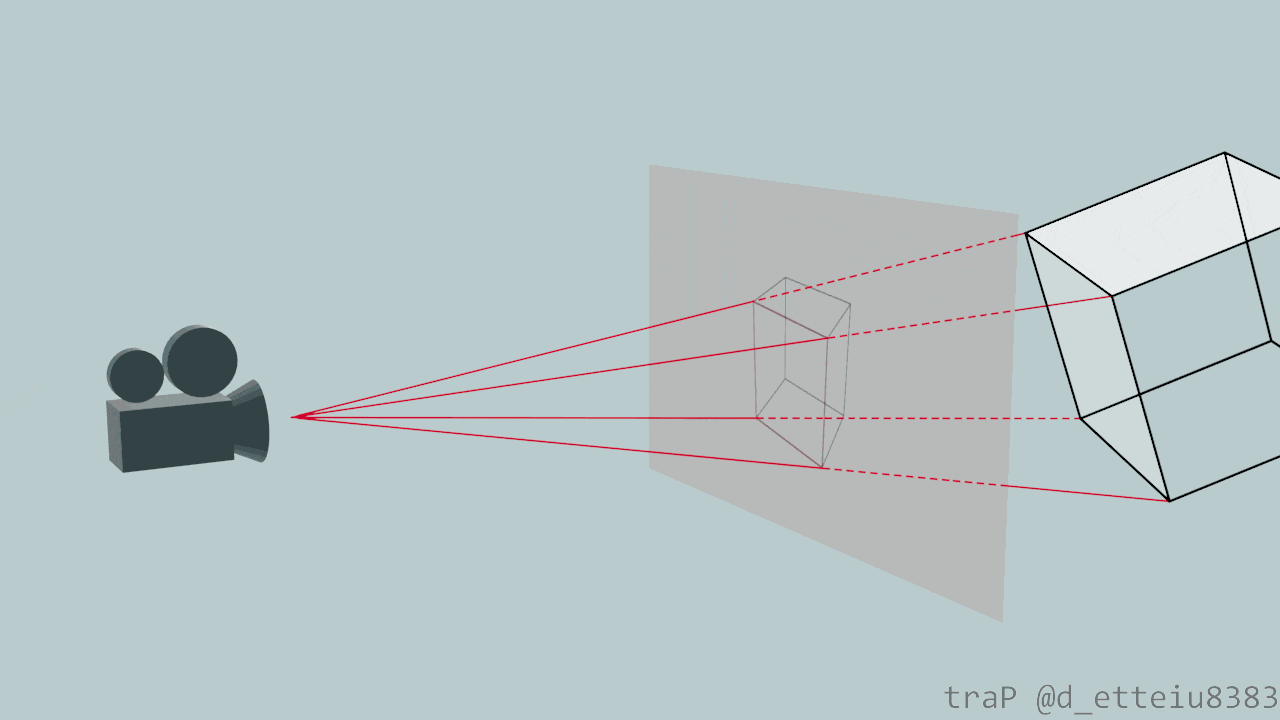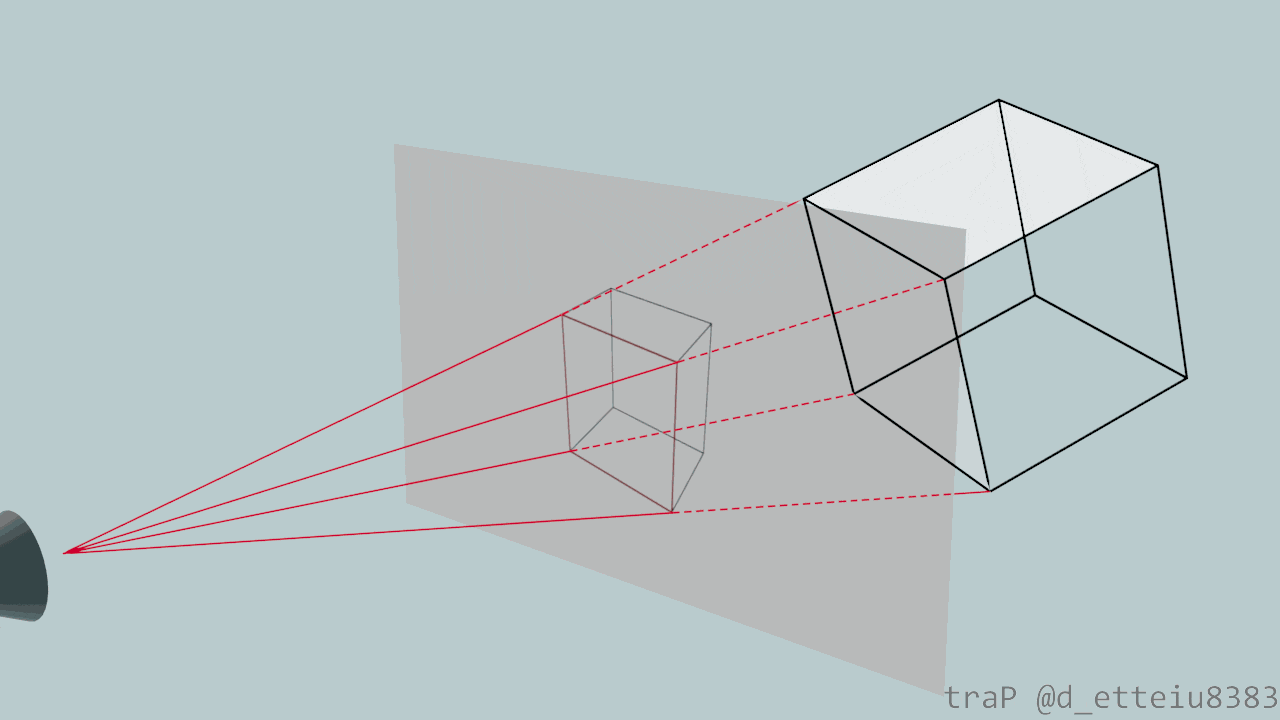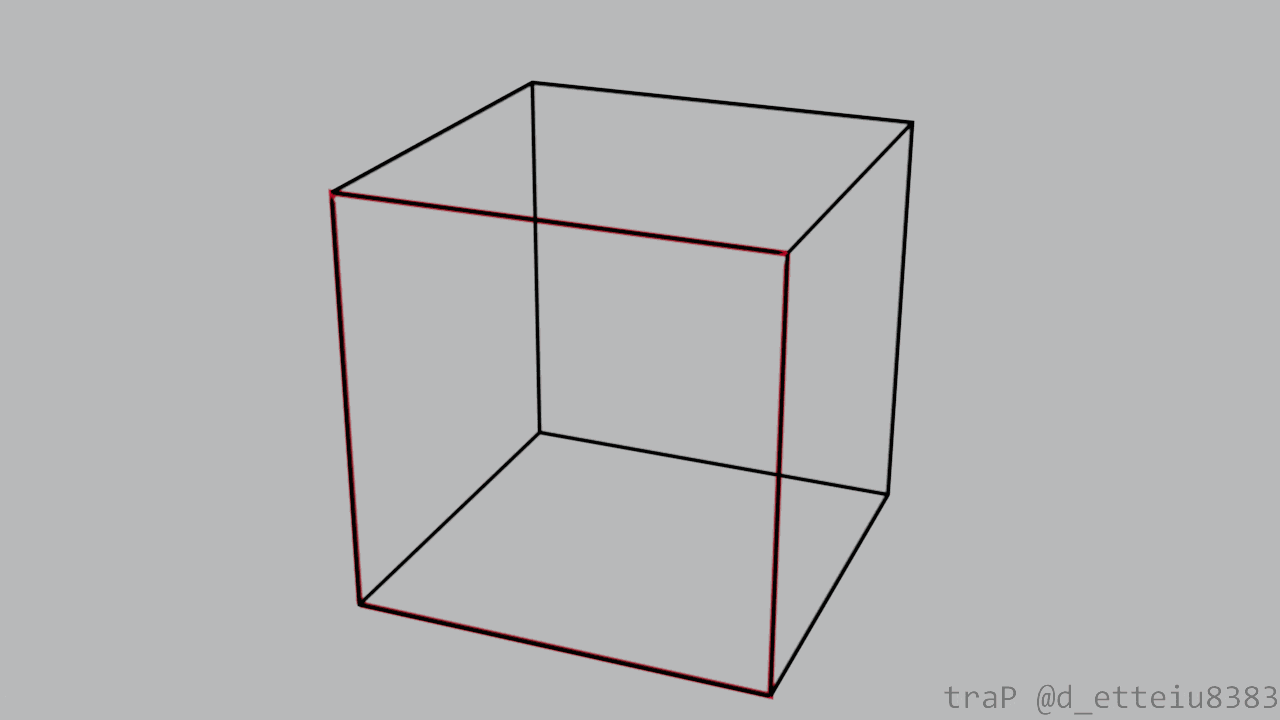
視点(カメラ)が3次元空間にあり、この視点と"見る対象"の間に平面があると仮定します。3次元空間上の対象をこの平面に移すことを考えます。対象から視点に届く光は直進してくるはずなので(今回は簡単のために屈折や反射を考えません)、3次元の空間中の点とカメラを直線で結んでみます。視点から見ると、この直線上にある点は全て同じ位置にあるように見え、区別できないはずです。区別できないなら、この直線上のどこに点を動かしても見える景色は変わらないはず。ということで、この直線と平面との交点に対象を移してしまいましょう。この移動を対象の各点に対して行うことで3次元空間上の対象を2次元空間に表現することができます。これは一般的に"透視投影"と呼ばれる図法です。確かに対象の点を平面に投影していますね。

"見る"の幾何学

で、まだこの説明だけでは"なぜ正方形が歪んで見えるのか"を説明できていません。今回考える"見る"をもっと厳密に、数学を使って考えてみましょう。

視点(カメラ)が3次元空間の原点にあり、$z$軸を上として$y$軸方向を向いているとします。$y=d$の平面に点$\mathrm{P}(x_{\mathrm{P}},y_{\mathrm{P}},z_{\mathrm{P}})$を移すことを考えます。移動後の点を${\mathrm{P}}^{\prime }(x_{{\mathrm{P}}^{\prime }},y_{{\mathrm{P}}^{\prime }},z_{{\mathrm{P}}^{\prime }})$としましょう。カメラの前にあるものだけ見たいので今回は $y_{\mathrm{P}}>0$ とします。

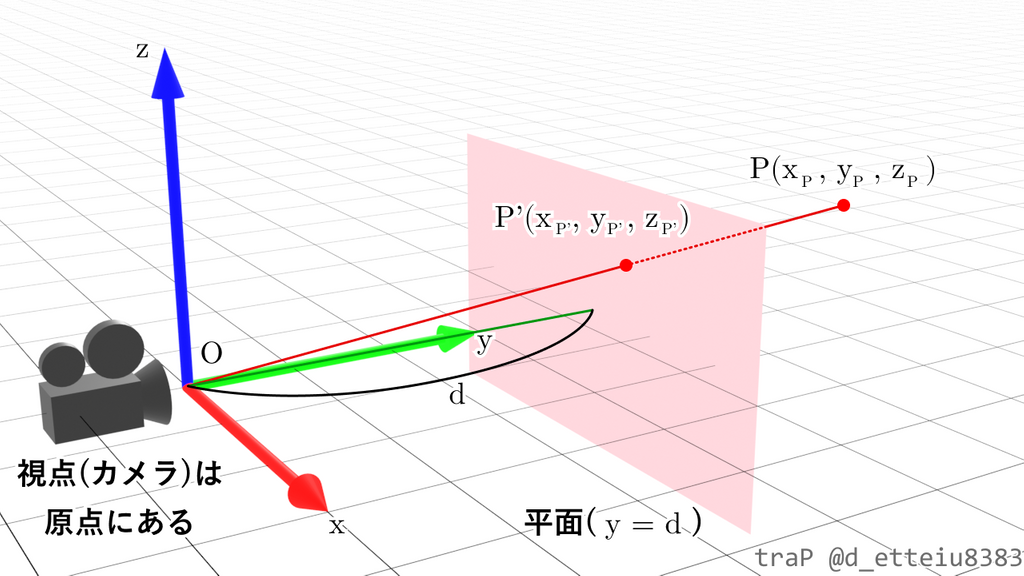
${\mathrm{P}}^{\prime }$は直線$\mathrm{OP}$上にあるはずです。直線$\mathrm{OP}$上の任意の点の位置ベクトルは $t\in \mathbb{R}$ をパラメーターとして、$(x,y,z)=t(x_{\mathrm{P}},y_{\mathrm{P}},z_{\mathrm{P}})$で表されます。${\mathrm{P}}^{\prime }$は平面上に存在するので $y_{{\mathrm{P}}^{\prime }}=d$ より $t=\frac{d}{y_{\mathrm{P}}}$ であり、 ${\mathrm{P}}^{\prime }=(d\frac{x_{\mathrm{P}}}{y_{\mathrm{P}}},d,d\frac{z_{\mathrm{P}}}{y_{\mathrm{P}}})$ であることがわかります。

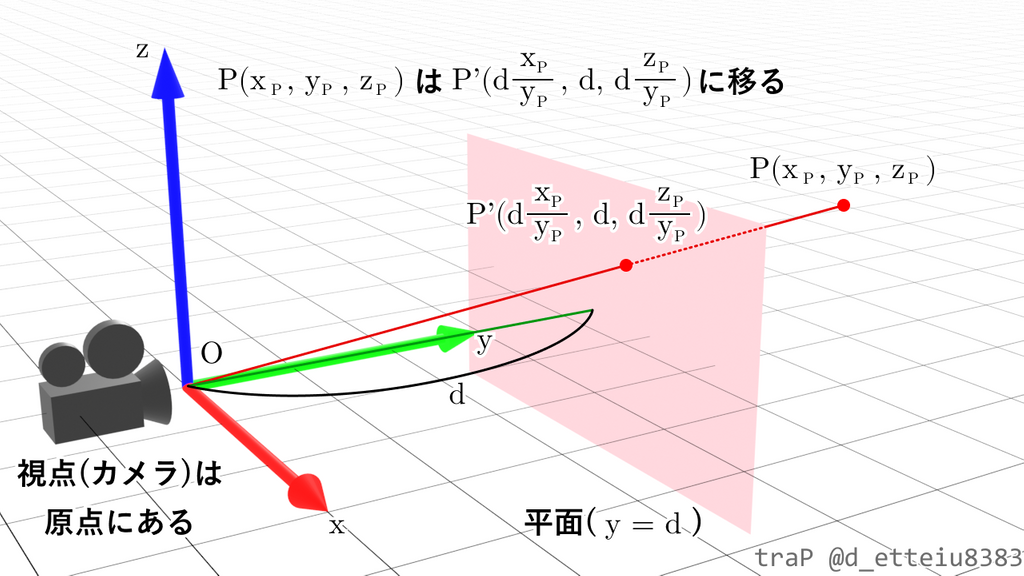
これで点$(x,y,z)$が点$(d\frac{x}{y},d,d\frac{z}{y})$に移ることがわかりました。今度は直線がどこに移るのか考えてみましょう。

点$\mathrm{P}(x_{\mathrm{P}},y_{\mathrm{P}},z_{\mathrm{P}})$を通り、方向ベクトル$\overrightarrow{u}=(x_u,y_u,z_u)$ に平行な直線は、$t\in \mathbb{R}$ をパラメーターとする媒介変数表示により、

$$\{\begin{array}{l}x=x_{\mathrm{P}}+t{x}_u\\ y=y_{\mathrm{P}}+t{y}_u\\ z=z_{\mathrm{P}}+t{z}_u\end{array}$$

と表せます。この直線上の各点について点の移動の場合と同じことが言えるので、直線は以下のように平面に移されます。

$$\{\begin{array}{l}x=d\cdot \frac{x_{\mathrm{P}}+t{x}_u}{y_{\mathrm{P}}+t{y}_u}\\ y=d\\ z=d\cdot \frac{z_{\mathrm{P}}+t{z}_u}{y_{\mathrm{P}}+t{y}_u}\end{array}$$

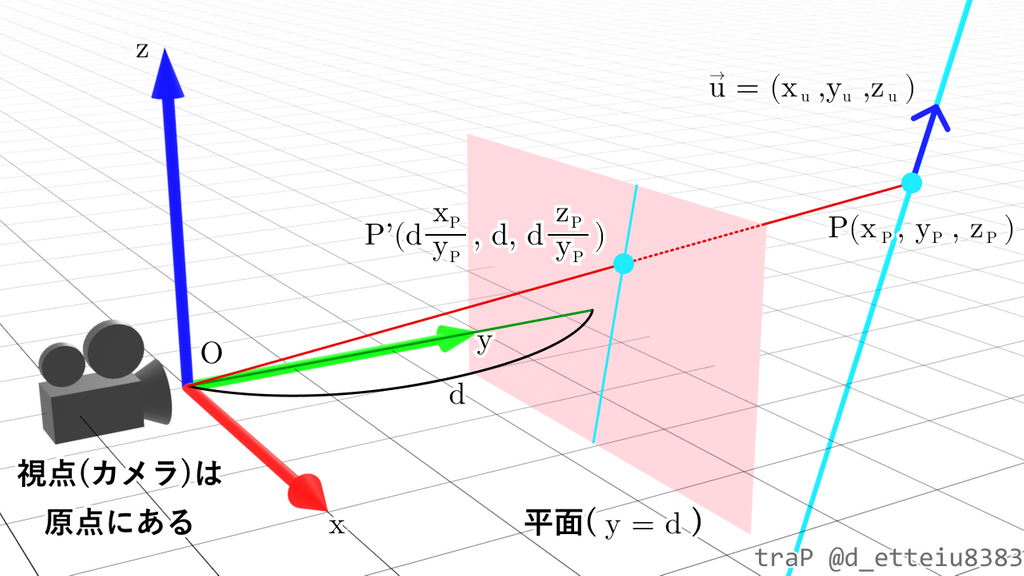
この直線の移動について、以下の二通りに場合を分けてどのような図形になるのか確かめてみましょう。

$y_u=0$ の時

$y_u=0$の時(直線の方向ベクトルが平面に平行なとき)、式から $t$ を消去すると、

$$\begin{array}{rl}y& =d\\ z& =\frac{z_u}{x_u}\left(x-d\cdot \frac{x_{\mathrm{P}}}{y_{\mathrm{P}}}\right)+d\cdot \frac{z_{\mathrm{P}}}{y_{\mathrm{P}}}\end{array}$$

と整理することができます。これは$y=d$の平面上に存在し、点$(d\cdot \frac{x_{\mathrm{P}}}{y_{\mathrm{P}}},d,d\cdot \frac{z_{\mathrm{P}}}{y_{\mathrm{P}}})$を通る、傾き$\frac{z_u}{x_u}$の直線ですね。つまり次のことがわかります。

投影する平面に平行な直線を投影すると、

• 平面内の直線に移る
• その傾きは方向ベクトルに依存する$(\frac{z_u}{x_u})$
• 通る点は元の3次元空間で通る点に依存する$(d\cdot \frac{x_{\mathrm{P}}}{y_{\mathrm{P}}},d,d\cdot \frac{z_{\mathrm{P}}}{y_{\mathrm{P}}})$

仮に空間上に、$y_u=0$であるような同じ方向ベクトルを持つ直線の組(つまり投影面に平行かつ、空間内で平行な直線の組)があるとき、全ての直線は投影後の平面内でも平行になることがわかります。

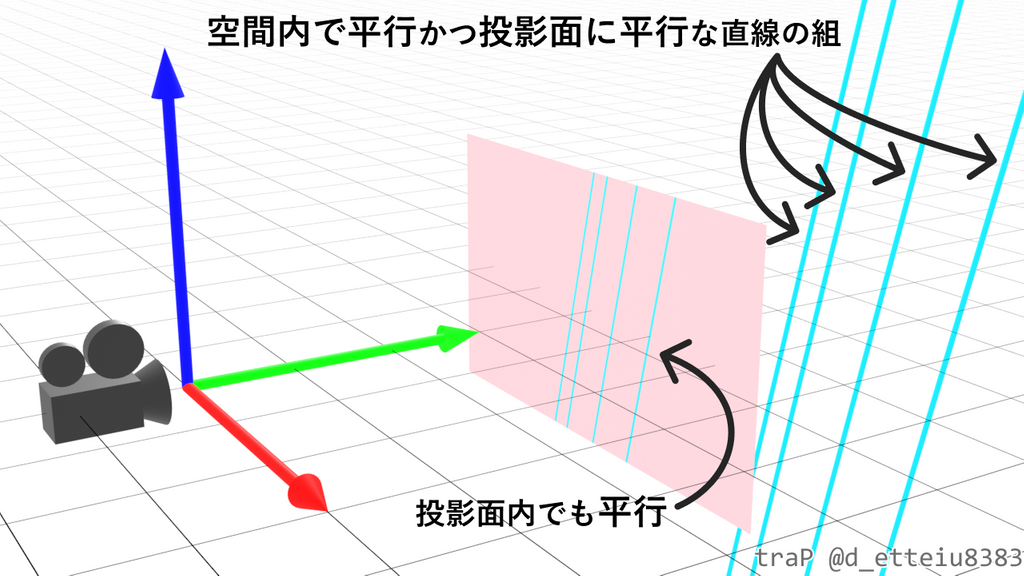
$y_u\ne 0$ の時

$y_u\ne 0$の時、式から$t$を消去するのが少し面倒なので代わりに$t\to \infty$としてみましょう。こうすることで、直線上の点が動くときに投影面内でどのように移されるのか何となくわかります。$t\to \infty$とすると、

$$\{\begin{array}{l}x\to d\cdot \frac{x_u}{y_u}\\ y=d\\ z\to d\cdot \frac{z_u}{y_u}\end{array}$$

となります。元の3次元空間上の直線の遠くの方の点は、方向ベクトルに依存する点$(d\cdot \frac{x_u}{y_u},d,d\cdot \frac{z_u}{y_u})$に近づいていくことがわかります。

投影する平面に平行でない直線を投影すると、

• 平面内の直線に移る(証明してないけど図とか見れば明らかですね())
• 元の3次元空間で通る点に関わらず、方向ベクトルに依存する点(消失点と呼ばれる)に収束する$(d\cdot \frac{x_u}{y_u},d,d\cdot \frac{z_u}{y_u})$

仮に空間上に、$y_u\ne 0$であるような同じ方向ベクトルを持つ直線の組(つまり投影面に平行でなく、かつ、空間内で平行な直線の組)があるとき、全ての直線は投影後の平面内で平行になるとは限らないが、ある1つの点に収束することがわかります。

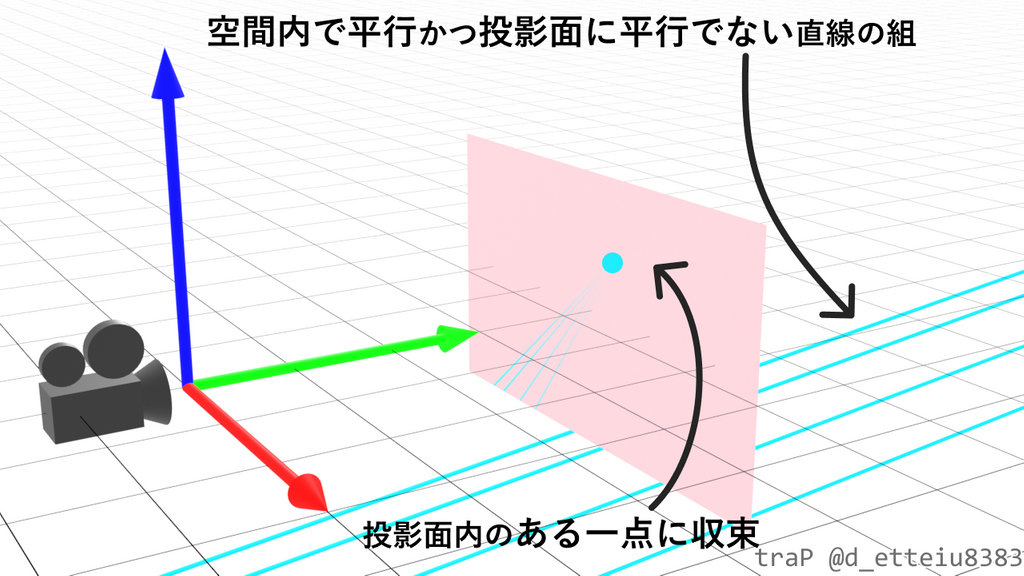
で、ようやく立方体の話に戻れますね。立方体は3組の平行な直線の組を持つ図形なので、それぞれの直線の組が投影面に平行かどうかにより、大きく分けて以下の3パターンの見え方になるはずです。

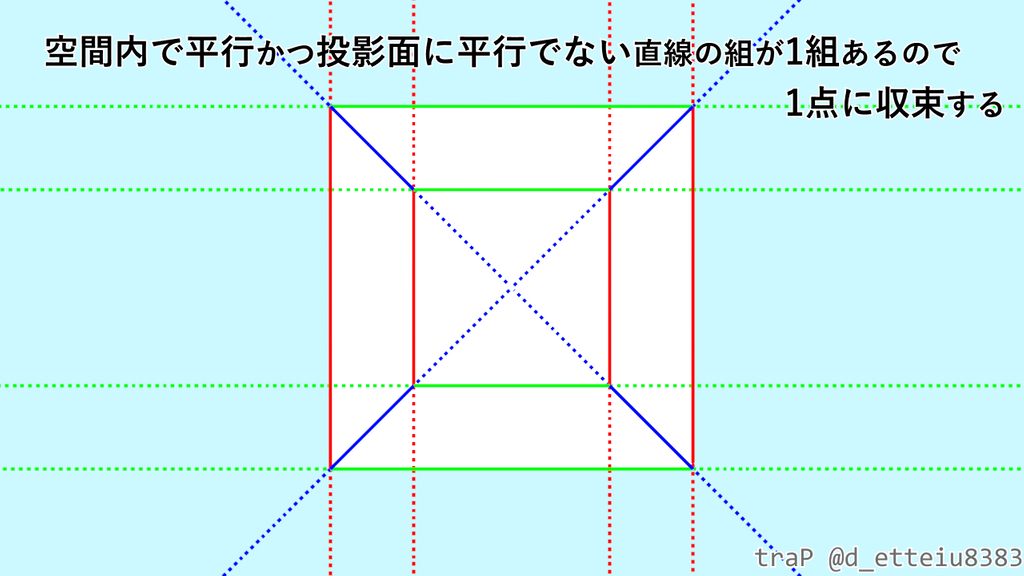
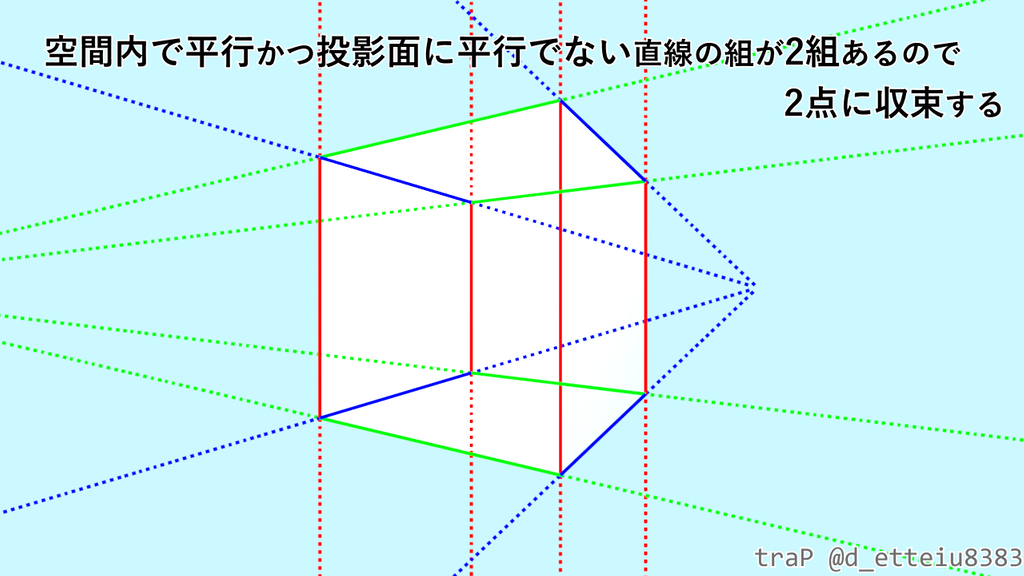
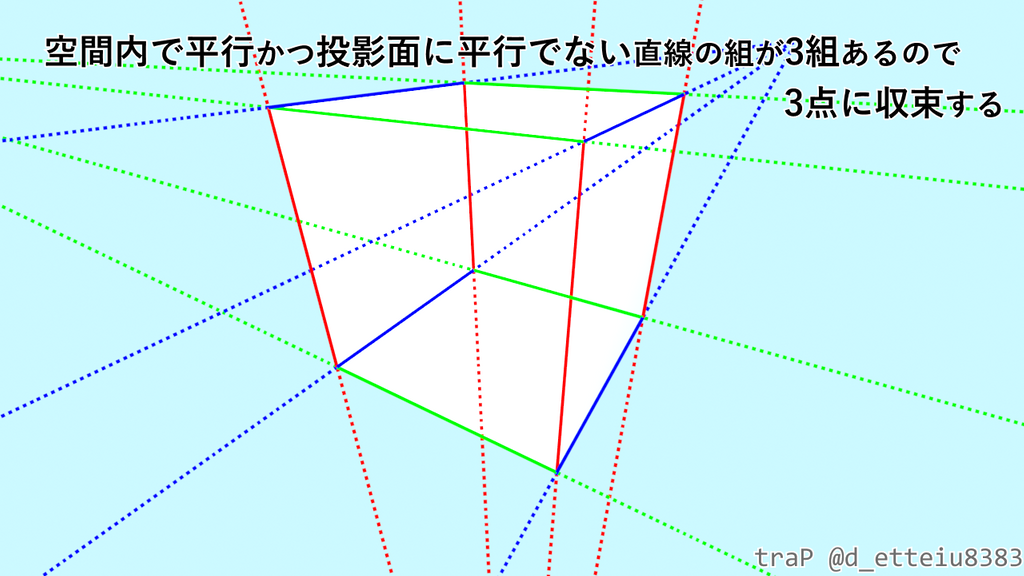
かなり回りくどくなってしまいましたが、3次元空間内で平行な直線の組は、透視図法により2次元平面に移した場合、2次元平面内でも平行になるとは限らない、だから空間上の正方形は歪んで"見えた"、ということを理解していただければ僕は満足です。

以下蛇足

で、今回話したかったことがあと2つだけあるので簡単にお話させていただきます。

n点透視図法とかいうやつ

学校の美術の時間なんかで「一点透視」「二点透視」「三点透視」というものを習った方も多いと思いますが、たまにこれが誤って使われているのを見かけます。特に見つけて悲しくなるのが「キャンバスに消失点は1~3つある」というもの。上の話から分かるように、透視図法における消失点は直線の方向ベクトルに依存するものであり、方向ベクトルの数だけ消失点があると言えます。例えば以下の図には100個の立方体が存在するので、原理的には300個の消失点が存在することになります。

一点透視、二点透視、三点透視は「世の中の大体の物は球か円筒か直方体っぽい形をしていて、平行線が最低3組あれば直方体を表せるしお絵描きに十分だから1~3つの消失点を使っていい感じにお絵描きできる」ってだけの話です。消失点は1つか2つか3つだと主張するものではありません。

3DCGと透視図法

今回のお話では数式を使いましたが、"計算できる"というのはとっても嬉しいことです。計算によって"見る"が達成できるということは、人間の目やカメラを使わずとも、コンピュータの計算によって画像を生成できるということです。3DCGの半分ぐらいは、今回使用した数式・理屈とほぼ同じことを行って3次元空間のオブジェクトを2次元の画像に表しています。ということで東京工業大学デジタル創作同好会traPでは、3DCGを利用したイラスト制作や、3Dモデルを用いたゲーム制作など、コンピューターグラフィックスに関する創作も行っています。興味のある方はぜひご入部ください。新歓イベントとして3Dモデリング体験会も予定していますので、新歓特設ページもぜひご覧ください。

参考文献

• 武蔵野美術大学　造形ファイル 透視投影http://zokeifile.musabi.ac.jp/透視投影/

明日の担当者はHmcmchくんです。お楽しみに。