Shape Sphere ~定期報告１~

どうも、D言語担当のそばやです。

我がサークルtraPでは期間を区切ってその期間ごとに別のゲームを制作することになっております。現在は2015年度第3期制作期間。今回紹介するゲームは「Shape Sphere」です。

この作品では主人公である「球」が敵と戦ったり仕掛けを解いたりしながら世界を救うという3Dアクションゲームです。その特徴として、自分も敵もガンガン「変形する」という点です。

forBlog4

さて、ここからは開発過程のお話をしたいと思います。

まず最初、主人公をゴムボールにしようというところから始まりました。つまり、主人公は基本は球で、押したら凹み、弾むということです。これを実現するには物理シミュレーションの勉強が必要かなぁと思い、人から話しを聞いたりしてまず作ったのがこのデモ。

physics

よく見ると点がいっぱい集まっているだけです。隣り合う点と点はバネとダンパーで繋がれています。

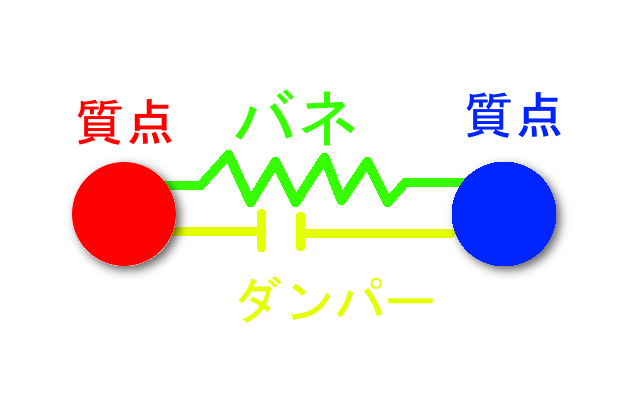
forBlog2

バネ(Spring)は高校の物理か何かで習う通り、「現在の長さと自然長との差」に比例して復元力を与える装置です。ダンパー(Damper)とは、(本物は)上にあるように途中に隙間が空いていて、中には油のようにドロっとした液体が入っています。これは隙間の両側の壁の速度の差に比例した力を与える装置です。

つまりあるバネについて自然長からの伸びを $x$ とすると、それによって与えられる力 $F_{s p r i n g}$ は、ある定数 $k$ を用いて、 $F_{s p r i n g} = - k x$ と表されます。また、あるダンパーについて、２つの質点の相対速度を $v$ とすると、それによって与えられる力 $F_{d a m p e r}$ は、ある定数 $c$ を用いて、 $F_{d a m p e r} = - c v$ と表されます。この２つの事実から、(細かい話は抜きにすると)この質点の運動方程式は $m \overset{x}{¨} + c \overset{x}{˙} + k x = 0$ となります。この微分方程式の解は実はm,k,cによって若干変わってきてしまうのですが、そこをうまい具合にとってあげると、解は $x = C e^{- α t} c o s (ω t + β)$ といった形で表されます。細かい定数の話は抜きにして定性的にこの式を眺めてみると、 $x$ は $e^{- t}$ と $c o s (t)$ の積であるということがわかります。 $e^{- t}$ は $x$ を0に収束させる作用、 $c o s (t)$ は $x$ を0の周りで振動させる作用です。これによって、質点はいわゆる減衰振動というやつをしてくれます。この運動の周期やエネルギー減衰率はm,k,cによって調整可能です。なのでこの装置は質点の動きを好きなように安定化させることができるという点で非常に便利なわけです。

とまぁこういう事前知識があったので、円形に並べた質点それぞれにバネダンパーをつけてやればゴムボールっぽくなるのでは？と思ったのですが、なかなかうまくいきません。上のサンプルはブニョブニョしすぎの饅頭みたいで、いまいち締まりがありません。もっと固くしてやろうとバネ定数とかをいじると爆発したり二重構造になってしまったりしてしまいます。

二重構造をとる質点たち

爆発するのは数値積分の精度が足りないせいなのですが、高精度の計算をしようとすると時間がかかります(といっても数十ミリ秒ほどですが)。ゲームで使うことを考えるとあまり時間をかけるわけにもいきません。

二重構造をとるのは、「それでも安定化する条件を満たすから」なんですよね。つまり、バネダンパーが保証してくれることは「隣り合う質点どうしの距離が一定になること」なので、このようにジグザグになるほうが楽ならばそのようになってしまうというわけです。

改良案として、内部から圧力をかけてやることにしました。よく考えたら風船とかもそういう風になっているわけですから、圧力がないのはおかしいです。

圧力を加えてみたやつ

いいかんじに固くなりました！やったぜ！これで2D版のデモができました。しかし、このゲームは本当は**D言語**製で、しかも3Dゲーム。このデモはJava製で、2D。ここから**D言語**のライブラリを整えたりするのにかなりの時間を要し、なんとか3D版のものを作りました。

はじめての3Dゴムボール

やったぜ！

この3D化にも一工夫要しました。2Dの「円」は等間隔に点を並べて構成するのはそう難しいことではありませんが、3Dの「球」を点をなるべく等間隔に配置するのは適当にやってできるものではないからです。一般によく思いつく3Dでの球の作り方は、極座標表示的なやつで、Blenderでは「UV球」と呼ばれています。

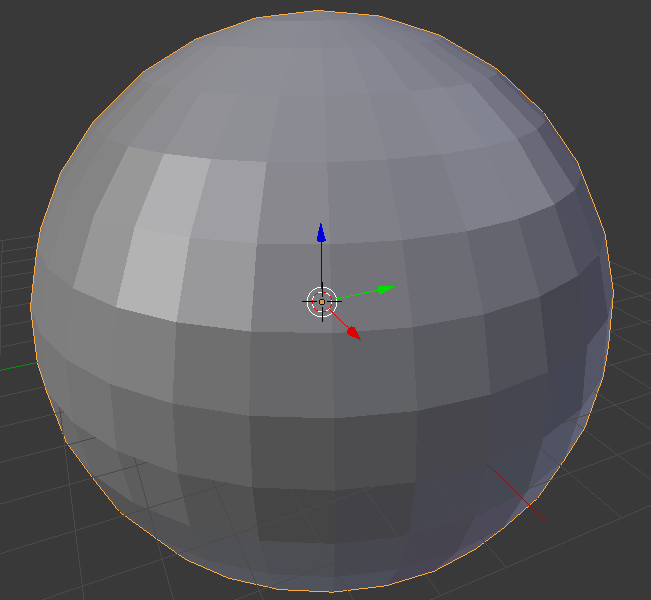BlenderでのUV球

$\theta , \phi$ を等間隔で刻みながら点を打っていくといった方式です。ですが、この方法では極付近と赤道付近での点の密集度が明らかに異なっています。球はなるべくどの方向からも均一な構造をとっていて欲しかったので、これはボツです(試してないけど)。

ということで、Blenderに標準搭載されているもう1つの球のほうを採用します。「ICO球(icosahedron)」です。

BlenderでのICO球

作り方は[こちらのサイト](http://blog.andreaskahler.com/2009/06/creating-icosphere-mesh-in-code.html)を参考にさせていただきました。見ての通り、全てのポリゴンは合同な正三角形です。生成法はともかくとして、こいつを使えば点と点を等間隔に配置できそうです。ということでこいつを採用しました。

その後動きに関して特に目立った技術的進歩はなく、ちょこちょこと調整を続け、見た目もかっちょよくしていただき、現在はこんなかんじに。

forBlog6

ぼよんぼよん。地面との当たり判定は、球を構成する全ての質点でやるというゴリ押しにより実現しています。仕方ないね。

プレイヤーの動きとしてはこんなところです。いまはチームメンバーがステージや画像、音楽などの素材を作ったり、敵を作ったりしてくれています。初公開は今年(2016年)10月に行われる工大祭を考えています。それまで乞うご期待！！！！

Shape Sphere ~定期報告１~

この記事をシェア

関連する記事