この記事は新歓ブログリレー2020 3日目の記事です。
ペンシルパズルってご存知ですか?ペンシルパズルとは紙に書いて解いていくパズルで、クロスワードや迷路、数独などがこれにあたります。
そこで今回は「四角に切れ」というペンシルパズルのソルバ(自分で解いてくれるプログラム)を作ってみました。といってもただ作るだけでは面白くないのでソルバの高速化のときに考えたことや解き方なども交えながら紹介していきたいと思います。
四角に切れってなに?
すごくざっくりと言うと「囲む」ゲームです。
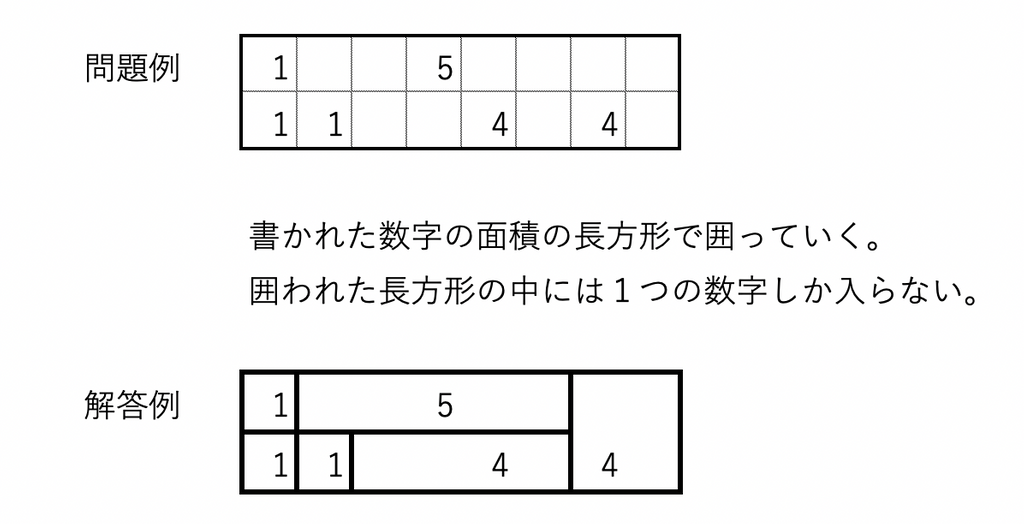
どう解くの?
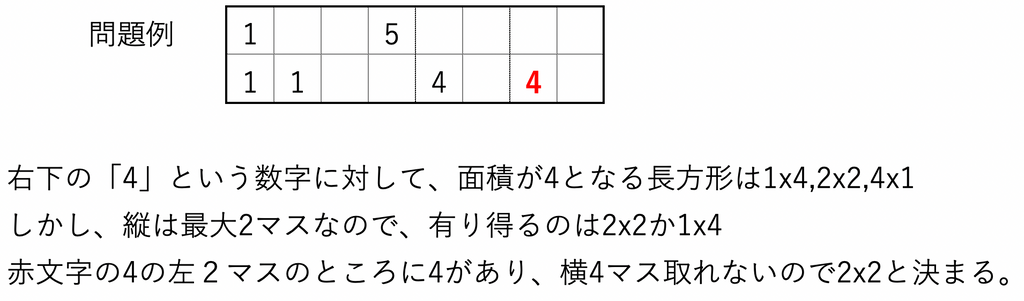
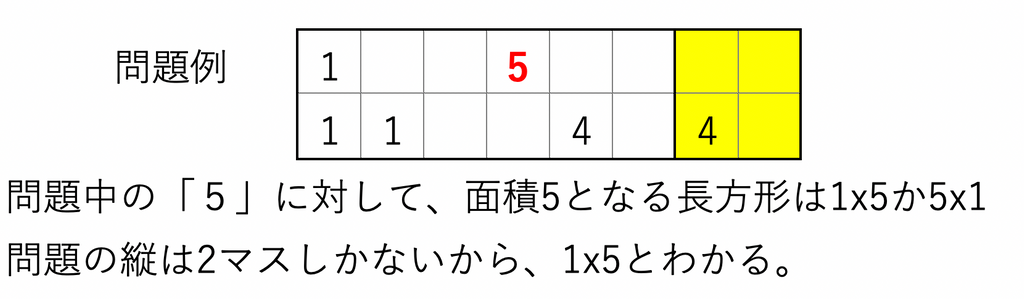
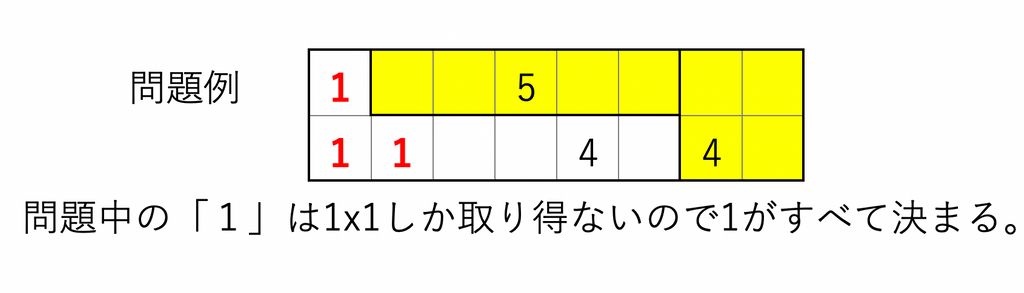
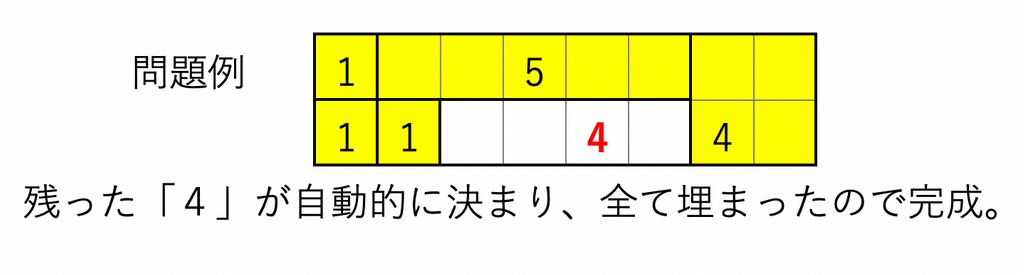
応用テクニックなどもあるのですが、とりあえずこれだけ覚えれば問題は解けるのでルール説明は以上です。(もちろん囲う長方形の辺は全て正の整数値です)
ソルバを作ろう。
ソルバを作るときに考えないといけないのは、「どういうふうに問題を解かせるか」です。
(これ以降説明で長方形で囲まれた部分をブロックと呼ぶことがあります。)
(ここでの長方形は、四隅がすべて直角の矩形のことを指します。そのため、正方形も長方形であるため、長方形という表現を使います)
その1. 力技でなんとかする(Depth-First Search)
あてはまるものから試してダメだったら他のところを埋めていく。
Depth-First Search(深さ優先探索)とは再帰関数を使って実装できる探索法です。
盤面とすでにおいたブロックの情報をもたせて、再帰を行い、全てのマスに全ての長方形が配置できれば終了です。
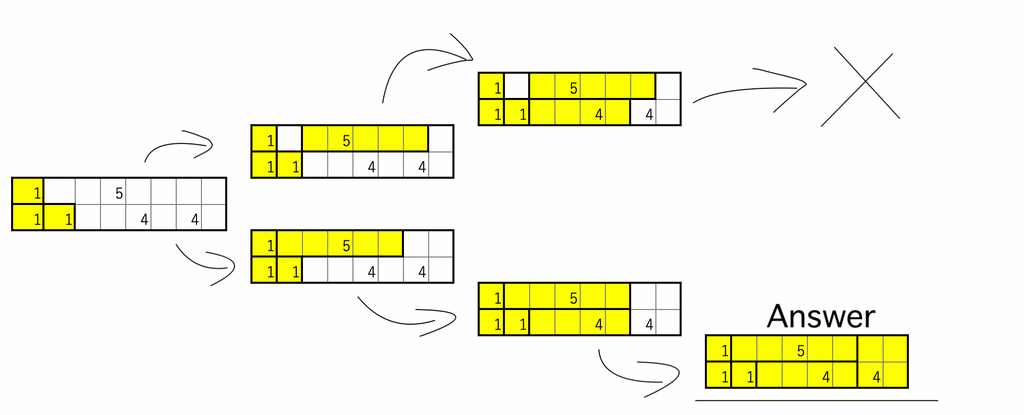
(↑こんな感じです)
この手法の問題点は、おけるところに手当り次第置いているところです。置く数が多いとすぐに組み合わせが爆発的に増え、比較的小さな盤面でも時間がかかってしまいます。
力技における高速化の手法
手法自体はそのままで、できるだけ高速化する手段を考えました。
長方形の縦横サイズを持っておく
このパズルは、すでに囲む長方形の面積が決まっているので、長方形の縦、横のサイズを事前に計算することができます。また、長方形の縦、横のいずれかが分かればもう片方の(縦が分かれば横も求まる)辺の長さも自動的に決まるので、長方形の縦または横をリストで持っておいて、必要になったらリストから値を取り出しするようにしました。(逐一素因数分解をしないで済むようになった)

置ける候補が少ないところから試して置いていく
置ける候補が少ないものとは一体どういうものでしょうか?例えば、面積が5や7や13といった素数の面積の長方形です。これらは、1x5または5x1、1x7または7x1、1x13または13x1のように長方形の形状に大きな制約をもった形です。素数の面積ほど大きな制約はないものの、素数×素数の面積のブロック(15や21、25など)も形のパターンが少ないです。
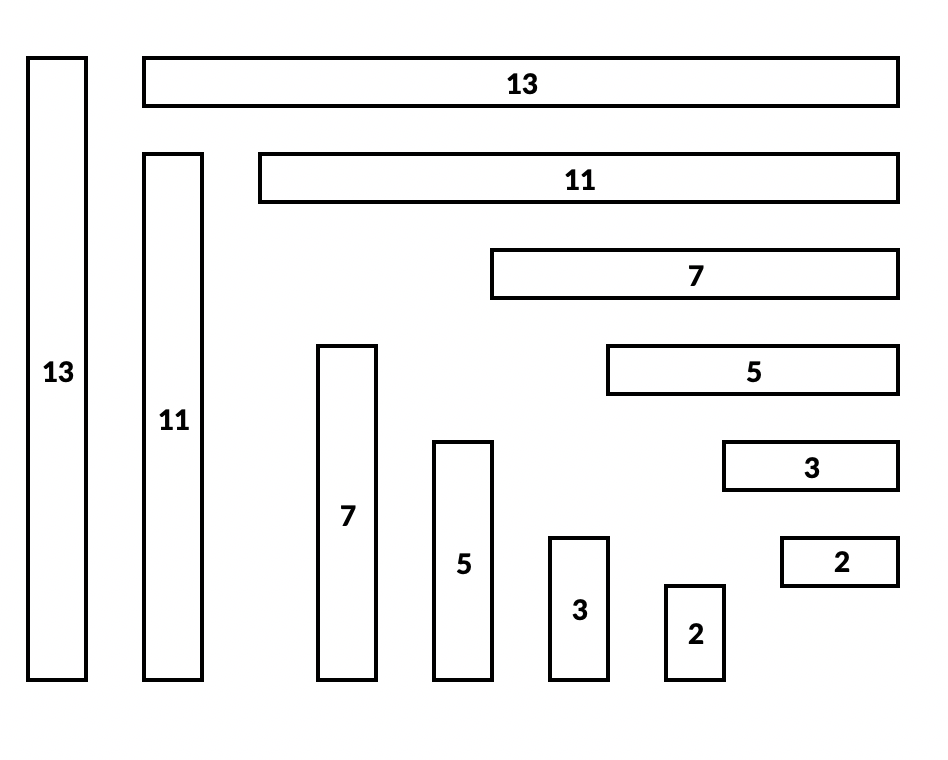
形状による制約だけでなく、周りに数字が多く存在し、縦横の大きさが限られているものも置ける候補が少ないです。
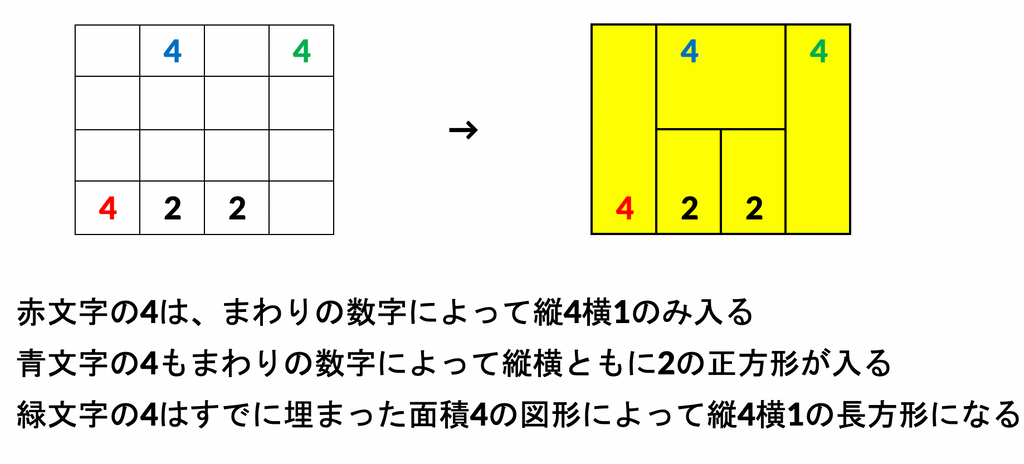
上の図において、最初に青文字の4のところは、青文字の4が「左上に来る場合」と、「右上に来る場合」の2通り考えられます。しかし、赤文字の4は1通りしかないため、縦4横1に確定します。これによって青文字の4は「数字が左上に来る場合」しか入らないことがわかり、確定します。
このように、候補が少なく、すぐに確定するものから置いていくことで他の長方形に対して置ける形の「新たな制約」が生まれます。これによって、まだ置いていない長方形に制約が増えることで置けるパターンが減り、試す組み合わせの数が減るため、高速化に寄与します。(ただし、問題のサイズが小さい場合は、置けるもののパターン数が少ない順にソートするところがボトルネックとなり逆におそいケースもありました。)
しかしこれらの高速化の工夫もむなしく、問題のサイズの大型化についていけずに解くのに時間がどんどん伸びてしまいました…(問題のケースによっても異なりますが、12x12位が限界でした)
その2.すぐに置けるところは確定させる(ブロック単位の決め打ち)
いままでの深さ優先探索はマシンパワーによる力技によって解いてきたため、少し複雑になるだけで計算時間がどんどん伸びてしまい、実用には遠く及びませんでした。
そこで、問題の一部に「置ける場所が一つに決まる」ところがいくつかあり、(ない場合もある)また、解いている途中にも1つに決まるところが出てくるため、それを優先的に埋め、制約を増やし、深さ優先探索の再帰の数をできるだけ減らすようにした。
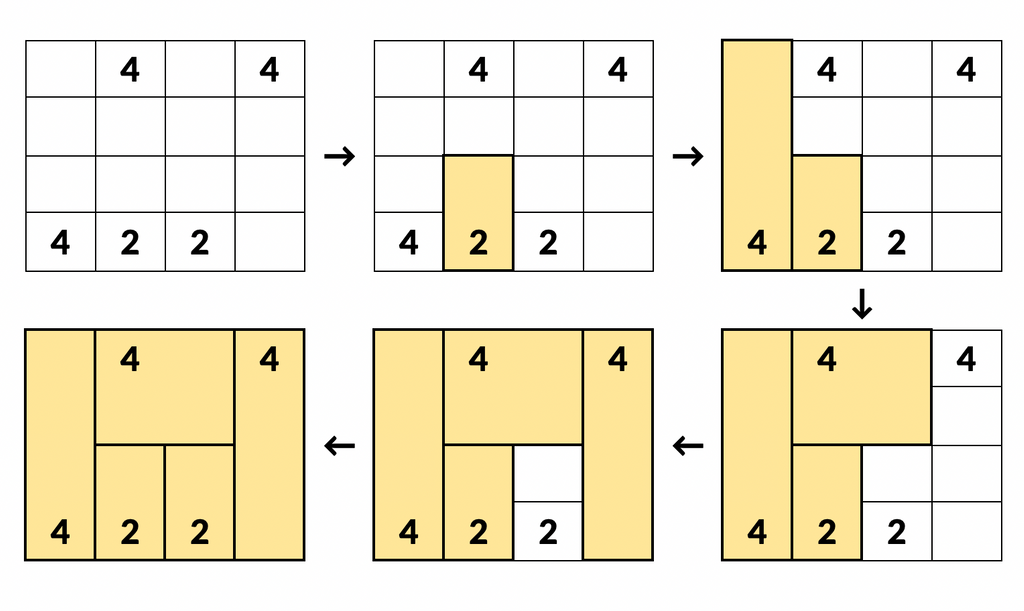
(決め打ちだけで決まる例)
決め打ちできる数は、問題によっても異なるし、最悪全く決め打ちができない場合はただの深さ優先探索と同程度の速度しか出ず根本的な高速化とはならなかった。(問題によっては、17x17でも1秒程度で求まっため、ある程度の成果はあるように思う?(DFSのみで150秒程度))
その3.マス単位での決め打ち(積集合埋め、和集合埋め)
ブロック単位での決め打ちは一定の効果はあったものの、やはり深さ優先探索をしているだけあって、問題の大型化についていけなかった。
そこでいままでと異なる着眼点から候補を決定していく。
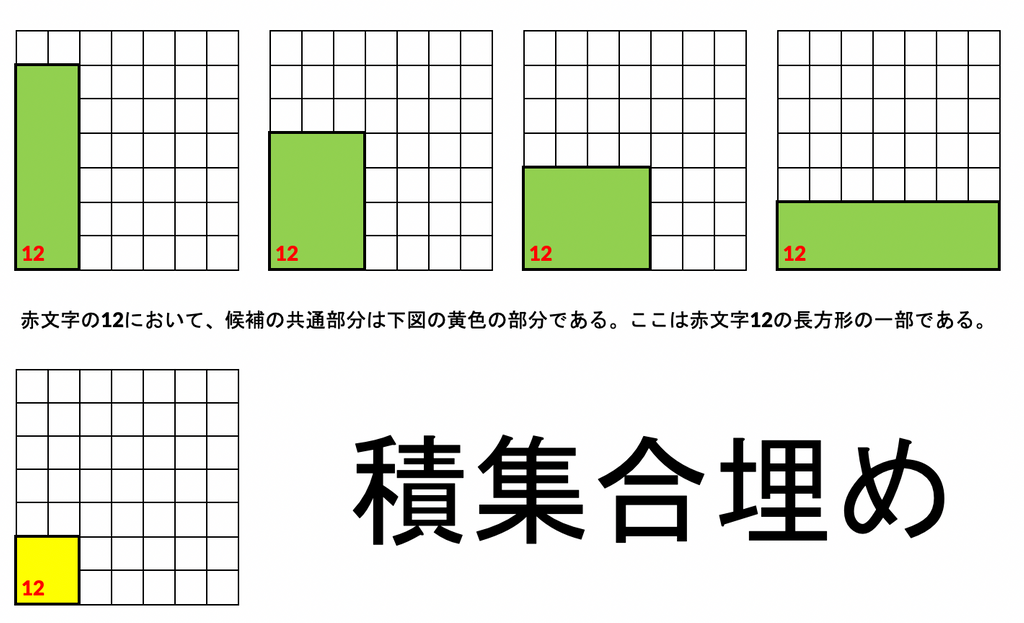
候補全てに共通する部分は、必ず存在する。(数字が書かれている部分が少なくとも全ての候補において共通なため)
積集合埋め(この記事ではそう呼ぶことにする)は、ある数字の置ける候補全てに共通する部分はある数字の領域に確定することを利用している。これによって、他の置けるブロックに制約が増えたので置けるパターンが減り他のものを埋まりやすくなる。
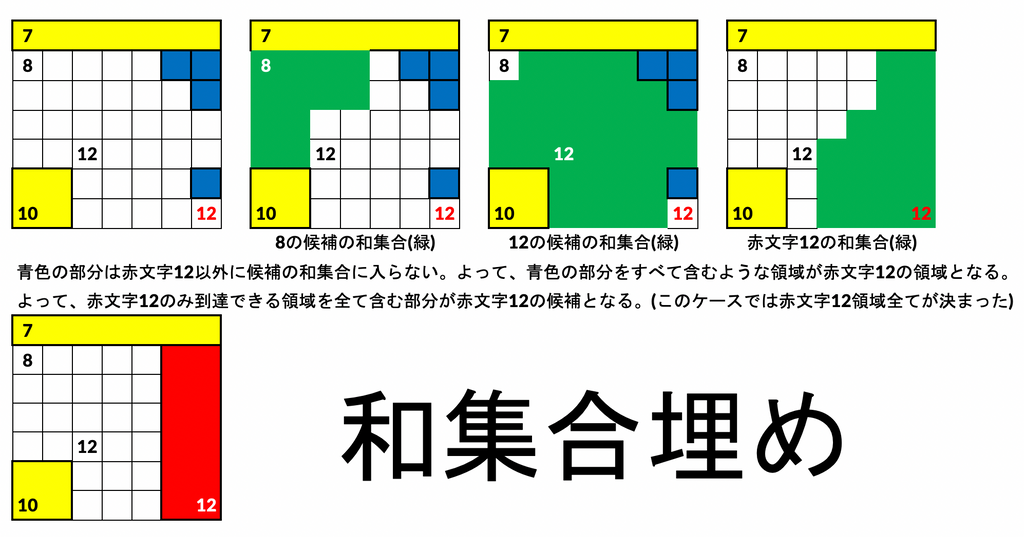
和集合埋め(この記事ではそう呼ぶことにする)は、ある数字によってのみ到達できる部分がある場合、そこはその数字の領域に確定することを利用している。
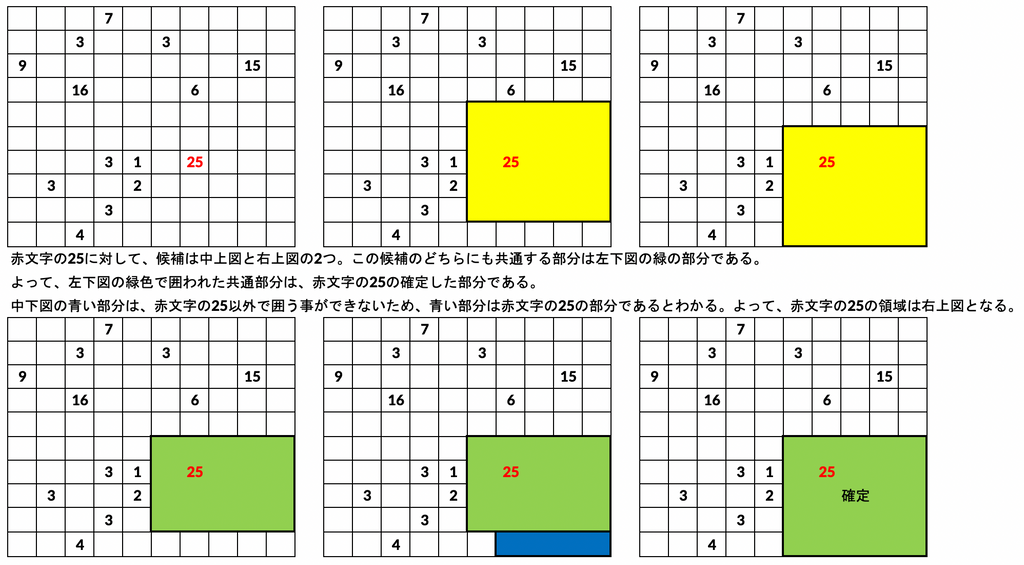
これは積集合埋めと和集合埋めによって面積25の正方形の場所を決定した例である。
これを利用することで、解を求めることができる。(複数解があるものは解が求まらない場合もある)(未証明)
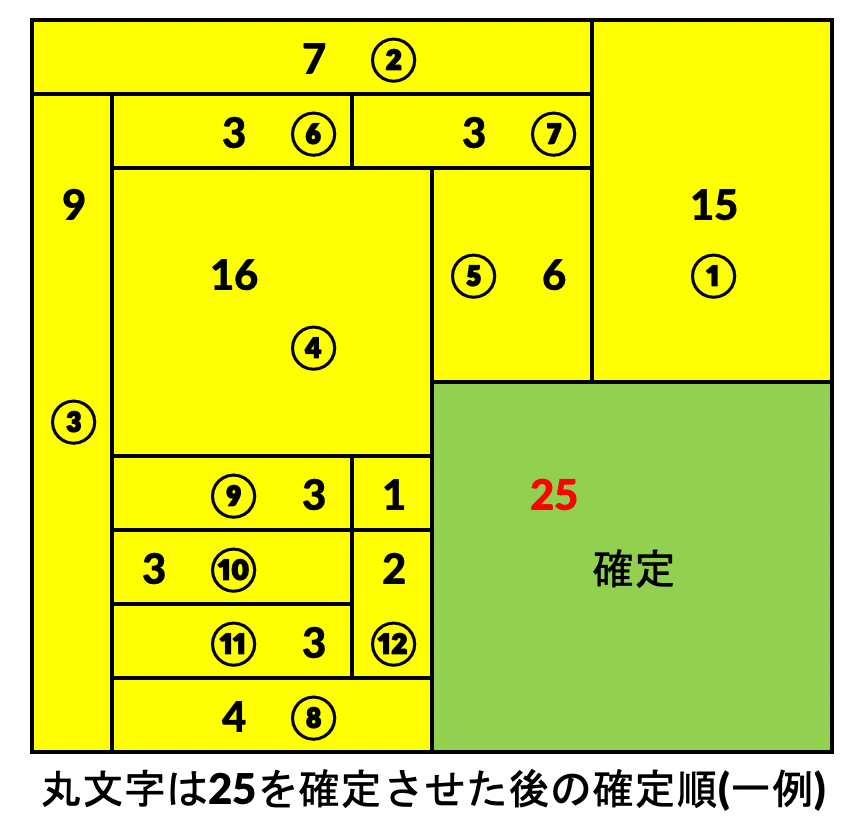
↑積集合埋め、和集合埋めで求めた例
この積集合埋め・和集合埋めは、紙に直接書き込んで試せる点において、人でもできることがわかります。
この積集合埋め・和集合埋めによって、17x17を5ms程度、40x25の巨大なパズルでも、15ms程度で解け非常に満足しております。(問題によって時間は変化する)
拙作ながらもを ソースコード置いておきます ワーハズカシ
実行速度の比較
問題によって大きく違うので一概に言えませんが、以下のようになりました。
| 実行時間(ms) | 10x10 | 17x17 | 18x26 | 25x40 |
|---|---|---|---|---|
| DFSのみ | - | - | ||
| ブロック決め打ち+DFS | - | |||
| 積集合埋め・和集合埋め |
ブロック単位の決め打ち+DFSのオーバーヘッドが大きいため、小さな盤面ではそれが大きく出た形となりました。
最後に
四角に切れソルバ、実は同じ部員の@idatenも書いていて、そこから助言をもらって完成させました。また、東工プロジェクトの方々にもパズルを解いてもらいありがとうございました。
参考文献
http://www.pro.or.jp/~fuji/puzzlelife/NumArea-Bridges.pdf
以上、Kejunでした。
明日は、NapoliNさんの記事です。楽しみ〜