feature image

2019年4月11日 | ブログ記事

立体でなにかする+おまけ【新歓ブログリレー2019 33日目】

新歓ブログリレー2019
Kejun icon Kejun

18のKejunです。
この記事は、「新歓ブログリレー」の記事です。

最近、どうやらが流行っている(?)ようなので自分もそれに乗っかってやってみました。

3DライブラリといってもOpenGLとかDirectXとかあるし、シェーダとかよくわからないので、できるだけローテクでやりたいというのがモチベーションです。

ということで、今回はProcessingで3Dオブジェクトを書いていきます。

おことわり
至らない部分もあります。（あったら指摘してもらうと嬉しいです）
画像の文字がすべて手書きになってしまった。

Processingとは

Javaっぽくて、グラフィック機能が補強されたようなものです。（ボキャ貧）
実はProcessingでもOpenGLは使えるのですが、頭が足りないので今回はデフォルトの描画ライブラリを使います。（逃げ）
ダウンロードはこちらから
processingの他の記事

どうやって3Dオブジェクトを描画するか

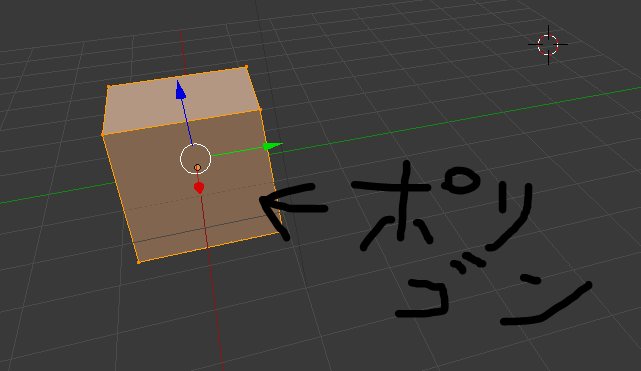
3Dオブジェクト（物体）はポリゴンという多角形によって構成されています。plg
なので、2Dの画面上に適当な色の適当な平面図形を描くことで3Dっぽく見せる事ができます。

すごく大雑把に言えば、見せたいオブジェクトと見せたい角度、位置にカメラを適当に置きます。
それでカメラに映る像を画面に描画すれば、やりたいことは実現できそうです。（下図）
cam
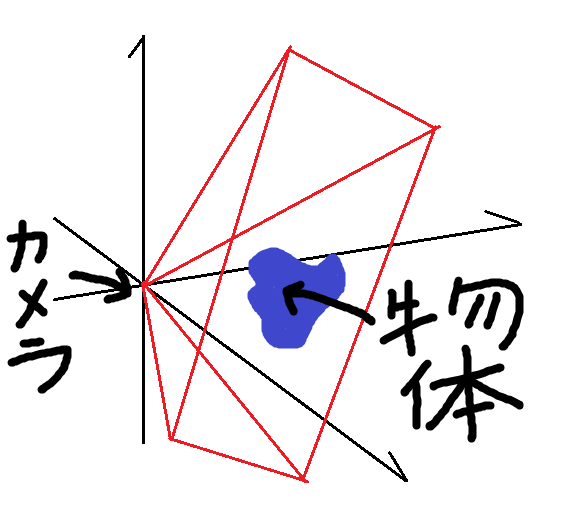
次は3Dの物体をカメラの像(2D)に落とし込みます（これが難しい）。
ですが、カメラや、物体の置く位置を工夫することで、3D→2D変換を非常に楽にすることができます。
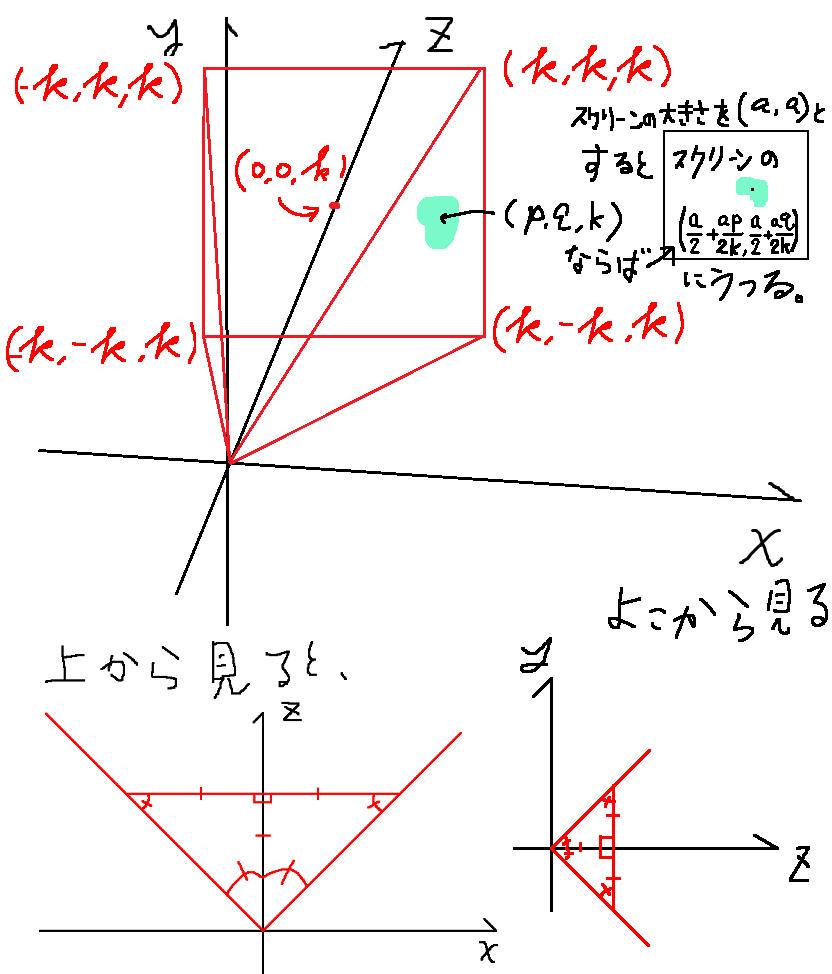
view-1-2
図を見ても分かりますが、要は、上下、左右を写すように画面を設計すれば、物体がにあり、
画面サイズが()、画面のに物体を描画すればいいことになります。
なので、このときに限って言えば、カメラを動かすよりも、物体を動かしたほうが何杯も楽であることが分かります。

描画

上につらつらと書かれている内容もやってみないと意味がないのでやってみる。
試しに、正四面体を回してみる。
正四面体は正六面体の一部の頂点を結んでできる。
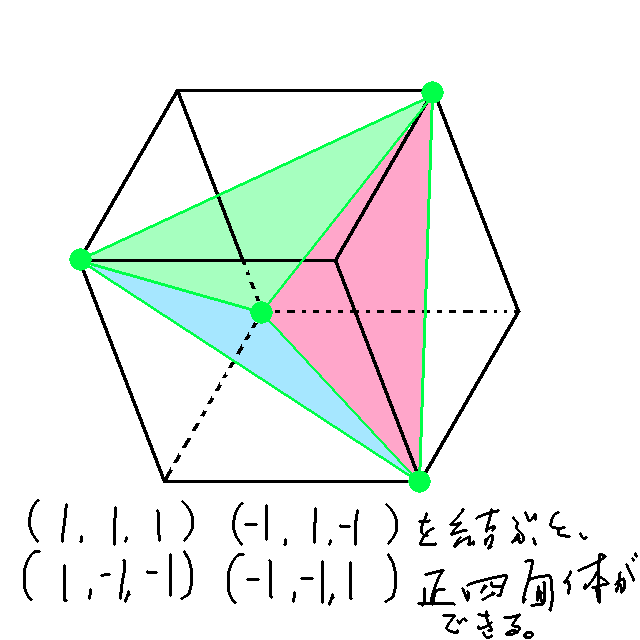
simen
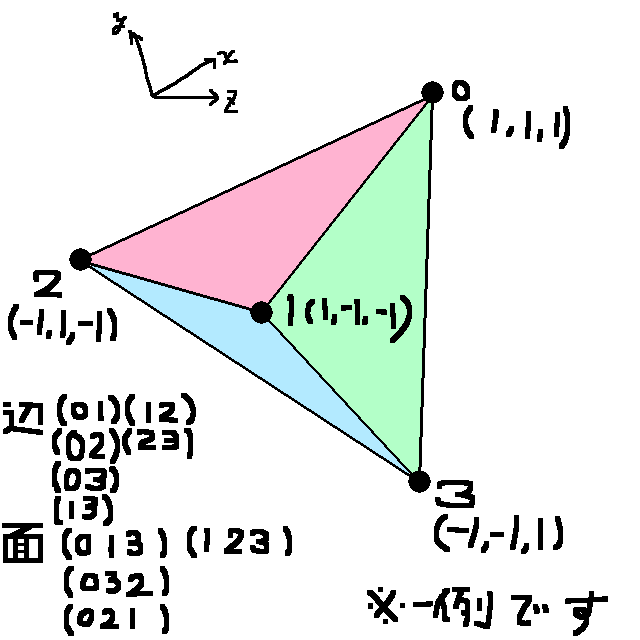
simen2-1
とりあえず、これをプログラムすると以下の通り

ソースコードは畳んでいます 
double[] center={0.0,0.0,4.0};  //立体の中心座標
double[][] vertex={
  {1,1,1},
  {1,-1,-1},
  {-1,1,-1},
  {-1,-1,1}
};      //中心座標からの相対座標
double rotate_angle=0;  //回転速度
long counter=0;
double[][] v_draw=new double[4][2];  //3次元から2次元に落とし込む
int[][] draw={
  {0,2},
  {0,1},
  {0,3},
  {1,2},
  {1,3},
  {2,3},
};

int[][] polygon={
  {0,1,3},
  {0,3,2},
  {0,2,1},
  {1,2,3}
};

void setup(){
  size(800,800);
  frameRate(60);
  background(0);
}

void draw(){
  background(0);
  convert3Dto2D();
  stroke(255);
  smooth();
  for(int i=0; i<6; i++){
    line((float)v_draw[draw[i][0]][0],(float)v_draw[draw[i][0]][1],(float)v_draw[draw[i][1]][0],(float)v_draw[draw[i][1]][1]);
  }
  counter++;
  counter%=720;
  rotate_angle=((float)counter);
}

void convert3Dto2D(){
  for(int i=0; i<4; i++){
    double tmpx=center[0]+vertex[i][0];
    double tmpy=center[1]+vertex[i][1];
    double tmpz=center[2]+vertex[i][2];
    v_draw[i][0]=400+400*(tmpx/Math.abs(tmpz));  //x
    v_draw[i][1]=400+400*(tmpy/Math.abs(tmpz));   //y　画面でいうと
  }
}

ap1
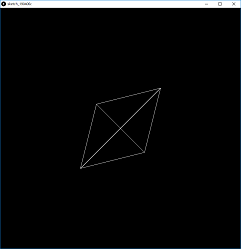
いちおう正四面体が現れましたが、これでは何も面白くないので、回してみたいと思います。

立体を回す

回転では行列を使うと便利で、今回はロドリゲスの回転公式を使う。
ロドリゲスの回転公式とは、
回転後の座標をとし、回転前の座標をとする。
また、回転軸のベクトルをとし、回転角度をとすると回転後の座標は以下のように表せる。

いかついがこの計算をすれば立体を回せるようになるようだ。
小数が絡むので誤差を蓄積しないように工夫もしないといけない。（計算用の変数を設けるだけ）

この回転を実装すると以下の通りである。

ソースコードは畳んでいます 
double[] center={0.0,0.0,4.0};  //立体の中心座標
double[][] vertex={
  {1,1,1},
  {1,-1,-1},
  {-1,1,-1},
  {-1,-1,1}
};      //中心座標からの相対座標

double[][] calc_V=new double[4][3];    //計算用の変数
double[] vec_unit_rotate={1/Math.sqrt(3),-1/Math.sqrt(3),1/Math.sqrt(3)};  //回転軸の単位ベクトル.
//下に行くとy座標が大きくなるので、y座標の回転軸のベクトルは-1倍することで、描画するときは、上がy座標が増える方向として描画される

double rotate_angle=0;  //回転速度
long counter=0;
double[][] v_draw=new double[4][2];  //3次元から2次元に落とし込む
int[][] draw={
  {0,2},
  {0,1},
  {0,3},
  {1,2},
  {1,3},
  {2,3},
};

int[][] polygon={
  {0,1,3},
  {0,3,2},
  {0,2,1},
  {1,2,3}
};
void setup(){
  size(800,800);
  frameRate(60);
  background(0);
}

void draw(){
  background(0);
  calc(rotate_angle,vec_unit_rotate);
  convert3Dto2D();
  stroke(255);
  smooth();
  for(int i=0; i<6; i++){
    line((float)v_draw[draw[i][0]][0],(float)v_draw[draw[i][0]][1],(float)v_draw[draw[i][1]][0],(float)v_draw[draw[i][1]][1]);
  }
  counter++;
  counter%=720;
  rotate_angle=((float)counter);
}

void convert3Dto2D(){
  for(int i=0; i<4; i++){
    double tmpx=center[0]+calc_V[i][0];
    double tmpy=center[1]+calc_V[i][1];
    double tmpz=center[2]+calc_V[i][2];
    v_draw[i][0]=400+400*(tmpx/Math.abs(tmpz));  //x
    v_draw[i][1]=400+400*(tmpy/Math.abs(tmpz));   //y　画面でいうと
  }
}

void calc(double ang,double[] vec){
  double c=Math.cos(ang*Math.PI/180);
  double s=Math.sin(ang*Math.PI/180);
  double[][] rotate_matrix={
      {c+vec[0]*vec[0]*(1-c)        ,vec[0]*vec[1]*(1-c)-vec[2]*s  , vec[0]*vec[2]*(1-c)+vec[1]*s},
      {vec[1]*vec[0]*(1-c)+vec[2]*s ,c+vec[1]*vec[1]*(1-c)         , vec[1]*vec[2]*(1-c)-vec[0]*s},
      {vec[2]*vec[0]*(1-c)-vec[1]*s ,vec[2]*vec[1]*(1-c)+vec[0]*s  , c+vec[2]*vec[2]*(1-c)}
  };
  
  for(int i=0; i<4; i++){
    for(int j=0; j<3; j++){
      double v=vertex[i][j];
      double ans=0;
      for(int k=0; k<3; k++){
        ans+=rotate_matrix[j][k]*vertex[i][k];
      }
      calc_V[i][j]=ans;
    }
  }
}

vlvgp-1i77t
迫真のBANDICAMくん。

面を描画する

いままでは頂点と辺しか描画していない。
なので面を描画する。
simen2-1

ソースコードは畳んでいます 
double[] center={0.0,0.0,4.0};  //立体の中心座標
double[][] vertex={
  {1,1,1},
  {1,-1,-1},
  {-1,1,-1},
  {-1,-1,1}
};      //中心座標からの相対座標

double[][] calc_V=new double[4][3];    //計算用の変数
double[] vec_unit_rotate={1/Math.sqrt(3),-1/Math.sqrt(3),1/Math.sqrt(3)};  //回転軸の単位ベクトル.
//下に行くとy座標が大きくなるので、y座標の回転軸のベクトルは-1倍することで、描画するときは、上がy座標が増える方向として描画される

double rotate_angle=0;  //回転速度
long counter=0;
double[][] v_draw=new double[4][2];  //3次元から2次元に落とし込む
int[][] draw={
  {0,2},
  {0,1},
  {0,3},
  {1,2},
  {1,3},
  {2,3},
};

int[][] polygon={
  {0,1,3},
  {0,3,2},
  {0,2,1},
  {1,2,3}
};
void setup(){
  size(800,800);
  frameRate(60);
  background(0);
}

void draw(){
  background(0);
  calc(rotate_angle,vec_unit_rotate);
  convert3Dto2D();
  stroke(255);
  smooth();
  for(int i=0; i < 4; i++){
      triangle((float)v_draw[polygon[i][0]][0],(float)v_draw[polygon[i][0]][1],(float)v_draw[polygon[i][1]][0],(float)v_draw[polygon[i][1]][1],(float)v_draw[polygon[i][2]][0],(float)v_draw[polygon[i][2]][1]);
  }
  
  counter++;
  counter%=720;
  rotate_angle=((float)counter);
}

void convert3Dto2D(){
  for(int i=0; i < 4; i++){
    double tmpx=center[0]+calc_V[i][0];
    double tmpy=center[1]+calc_V[i][1];
    double tmpz=center[2]+calc_V[i][2];
    v_draw[i][0]=400+400*(tmpx/Math.abs(tmpz));  //x
    v_draw[i][1]=400+400*(tmpy/Math.abs(tmpz));   //y　画面でいうと
  }
}

void calc(double ang,double[] vec){
  double c=Math.cos(ang*Math.PI/180);
  double s=Math.sin(ang*Math.PI/180);
  double[][] rotate_matrix={
      {c+vec[0]*vec[0]*(1-c)        ,vec[0]*vec[1]*(1-c)-vec[2]*s  , vec[0]*vec[2]*(1-c)+vec[1]*s},
      {vec[1]*vec[0]*(1-c)+vec[2]*s ,c+vec[1]*vec[1]*(1-c)         , vec[1]*vec[2]*(1-c)-vec[0]*s},
      {vec[2]*vec[0]*(1-c)-vec[1]*s ,vec[2]*vec[1]*(1-c)+vec[0]*s  , c+vec[2]*vec[2]*(1-c)}
  };
  
  for(int i=0; i < 4; i++){
    for(int j=0; j < 3; j++){
      double v=vertex[i][j];
      double ans=0;
      for(int k=0; k < 3; k++){
        ans+=rotate_matrix[j][k]*vertex[i][k];
      }
      calc_V[i][j]=ans;
    }
  }
}

vtxki-bqy7f
これでとりあえず、絶えず変形し続ける多角形が映るはずである（本当は正四面体が写っているが全面同じ色なので立体感が皆無）

描画量を減らす と 陰影

立体感を出すための陰影、より高速に描画することが目標。
まずは、描画量削減から。
いま回している物体は単純なのでそこまで描画が遅いとは感じないが、
複雑な物体になるとそうはいかない。
なので、できるだけ描画するものを減らすことでその処理が軽くなる。

その仕組は、ポリゴンの表裏を考えることにある。
これだけではよくわからないので、具体例を挙げて説明したい。
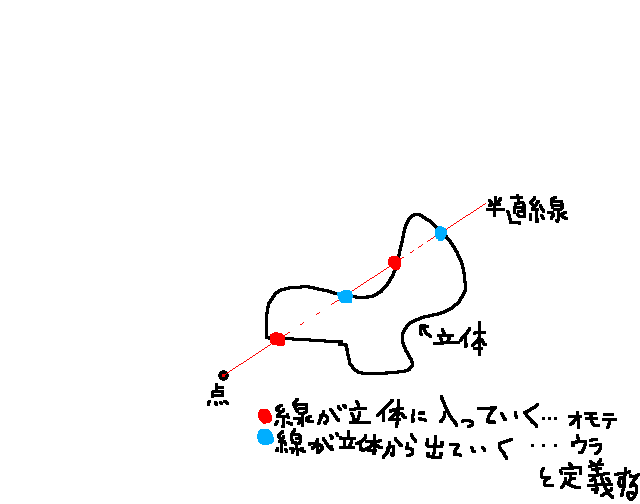
lang2
ウラはオモテに隠れている。
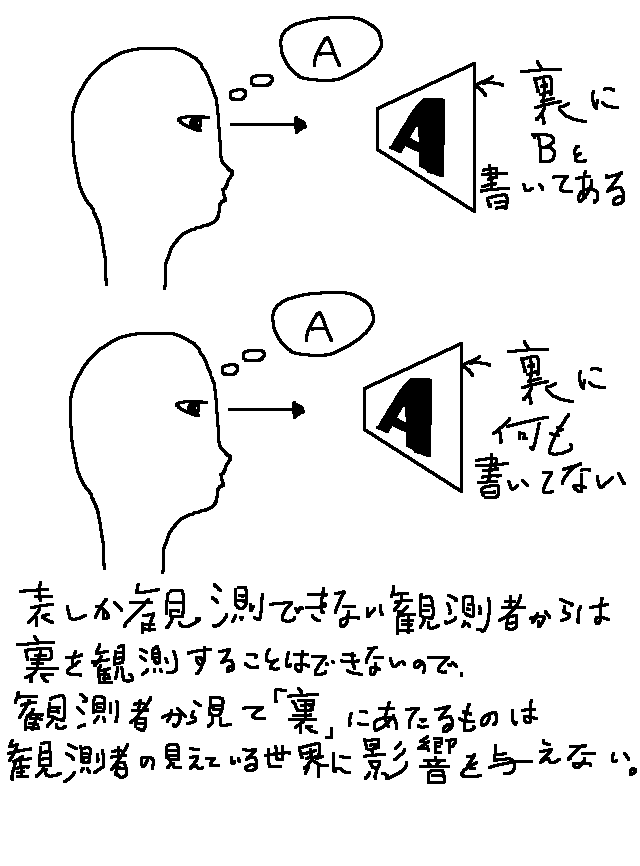
karingusetumei
ここで描くのはすべて不透明のポリゴンなので、ウラはオモテに完全に隠れて観測者からは見えない。
なので、立体のオモテに当たる部分だけ描画すれば見栄えには影響しない。
次に表裏の判定の大雑把な仕組み。
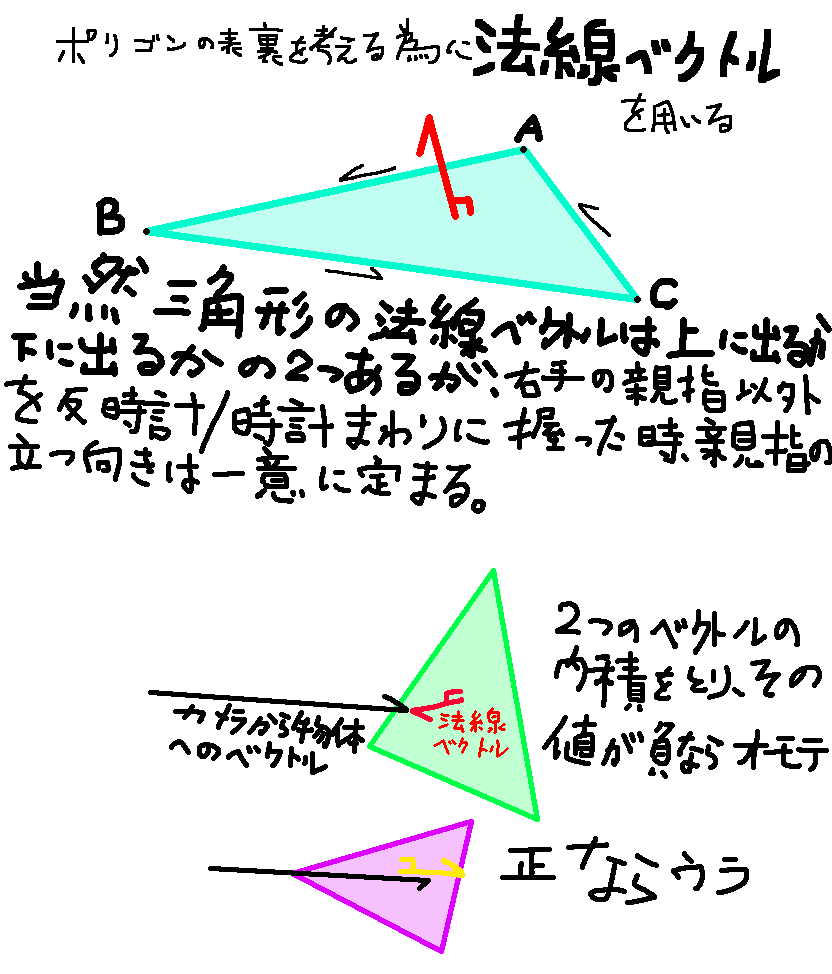
omoteura

法線ベクトルの導出はここをご覧下さい。
モデルによっては面が時計回りなのに反時計回り前提で処理した場合、内積の正負が逆になるので表判定が内積が正であることのときもある。
↓カリング（わかりやすいように表裏判定で一部表も描画しないようにしている）
sqv14-ltigq

次に、陰影です。
あまり面倒なことを考えたくないので、カメラと同じ位置に光源があるとする。
現実の世界の光の反射とかを考える能力はないので、さっきのカリングで使った内積の値を使えないか考えた。

カメラから物体への単位ベクトルと、ポリゴンの単位法線ベクトルの内積の値はをとり、その絶対値を取ったときの値を光の強さとして描画するところうまいこといったのでそういうことにしておいた。（適当）
ytzytz2
ytz3
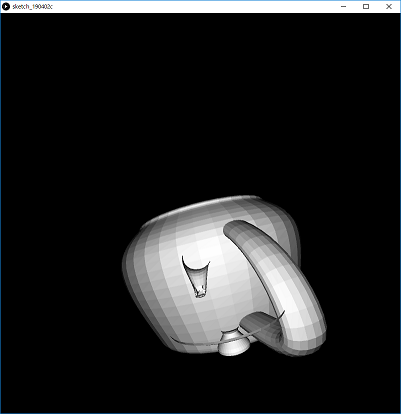
（座標の前後関係は全く実装してないので破綻している）
やったぜ。
カリングを実装したコード

ソースコードは畳んでいます 
import java.util.*;

double[] center={0.0,0.0,4.0};  //立体の中心座標
double[][] vertex={
  {1,1,1},
  {1,-1,-1},
  {-1,1,-1},
  {-1,-1,1}
};      //中心座標からの相対座標

double[][] calc_V=new double[4][3];    //計算用の変数
double[] vec_unit_rotate={1/Math.sqrt(3),-1/Math.sqrt(3),1/Math.sqrt(3)};  //回転軸の単位ベクトル.
//下に行くとy座標が大きくなるので、y座標の回転軸のベクトルは-1倍することで、描画するときは、上がy座標が増える方向として描画される

double rotate_angle=0;  //回転速度
long counter=0;
double[][] v_draw=new double[4][2];  //3次元から2次元に落とし込む
int[][] draw={
  {0,2},
  {0,1},
  {0,3},
  {1,2},
  {1,3},
  {2,3},
};

int[][] polygon={
  {0,1,3},
  {0,3,2},
  {0,2,1},
  {1,2,3}
};

double kyoudo=0;
void setup(){
  size(800,800);
  frameRate(60);
  background(0);
}

void draw(){
  background(0);
  calc(rotate_angle,vec_unit_rotate);
  convert3Dto2D();
  //draw_queue.sort(Comparator.comparing(V->V.zcord));
  stroke(255);
  smooth();
  for(int i=0; i < 4; i++){
    if(culling(polygon[i])){
      fill((int)(255*kyoudo));
      stroke((int)(255*kyoudo));
      triangle((float)v_draw[polygon[i][0]][0],(float)v_draw[polygon[i][0]][1],(float)v_draw[polygon[i][1]][0],(float)v_draw[polygon[i][1]][1],(float)v_draw[polygon[i][2]][0],(float)v_draw[polygon[i][2]][1]);
    }
    
  }
  
  counter++;
  counter%=720;
  rotate_angle=((float)counter);
}

void convert3Dto2D(){
  for(int i=0; i < 4; i++){
    double tmpx=center[0]+calc_V[i][0];
    double tmpy=center[1]+calc_V[i][1];
    double tmpz=center[2]+calc_V[i][2];
    v_draw[i][0]=400+400*(tmpx/Math.abs(tmpz));  //x
    v_draw[i][1]=400+400*(tmpy/Math.abs(tmpz));   //y　画面でいうと
  }
}

void calc(double ang,double[] vec){
  double c=Math.cos(ang*Math.PI/180);
  double s=Math.sin(ang*Math.PI/180);
  double[][] rotate_matrix={
      {c+vec[0]*vec[0]*(1-c)        ,vec[0]*vec[1]*(1-c)-vec[2]*s  , vec[0]*vec[2]*(1-c)+vec[1]*s},
      {vec[1]*vec[0]*(1-c)+vec[2]*s ,c+vec[1]*vec[1]*(1-c)         , vec[1]*vec[2]*(1-c)-vec[0]*s},
      {vec[2]*vec[0]*(1-c)-vec[1]*s ,vec[2]*vec[1]*(1-c)+vec[0]*s  , c+vec[2]*vec[2]*(1-c)}
  };
  
  for(int i=0; i < 4; i++){
    for(int j=0; j < 3; j++){
      double v=vertex[i][j];
      double ans=0;
      for(int k=0; k < 3; k++){
        ans+=rotate_matrix[j][k]*vertex[i][k];
      }
      calc_V[i][j]=ans;
    }
  }
}
boolean culling(int[] poly) {    //カリング（描画量を減らす）
  double[] cen={0, 0, 0};  //カメラ
  double[] vert={0, 0, 0};
  double c_d=0;
  double v_d=0;
  for (int i=0; i<3; i++) {
    for (int j=0; j<3; j++) {
      cen[i]+=calc_V[poly[j]][i];
    }
    cen[i]/=3.0;
  }
  for (int i=0; i<3; i++) {
    cen[i]+=center[i];
  }
  c_d=(float)Math.sqrt(cen[0]*cen[0]+cen[1]*cen[1]+cen[2]*cen[2]);
  for (int i=0; i<3; i++) {
    cen[i]/=c_d;
  }

  double[] v1={calc_V[poly[1]][0]-calc_V[poly[0]][0], calc_V[poly[1]][1]-calc_V[poly[0]][1], calc_V[poly[1]][2]-calc_V[poly[0]][2]};
  double[] v2={calc_V[poly[2]][0]-calc_V[poly[0]][0], calc_V[poly[2]][1]-calc_V[poly[0]][1], calc_V[poly[2]][2]-calc_V[poly[0]][2]};

  vert[0]=v1[1]*v2[2]-v1[2]*v2[1];
  vert[1]=v1[2]*v2[0]-v1[0]*v2[2];
  vert[2]=v1[0]*v2[1]-v1[1]*v2[0];  //法線ベクトル

  v_d=(float)Math.sqrt(vert[0]*vert[0]+vert[1]*vert[1]+vert[2]*vert[2]);
  for (int i=0; i<3; i++) {
    vert[i]/=v_d;
  }
  double cul=cen[0]*vert[0]+cen[1]*vert[1]+cen[2]*vert[2];
  kyoudo=Math.abs(cul);
  if (kyoudo>1) {
    kyoudo=1;
  }
  if (cul>-0.005) {

    return true;
  } else {
    return false;
  }
}

おまけ

東工大に入ってからTeXを使う頻度が増えると、TeXで表を書かないといけないことって出てきますよね？（少なくとも自分はそうでした）
なので、TeXでもっと楽に表が作れてたらなと思って、JavaでTeXの表作成支援ツールを作りました。（需要自分以外なさそう）
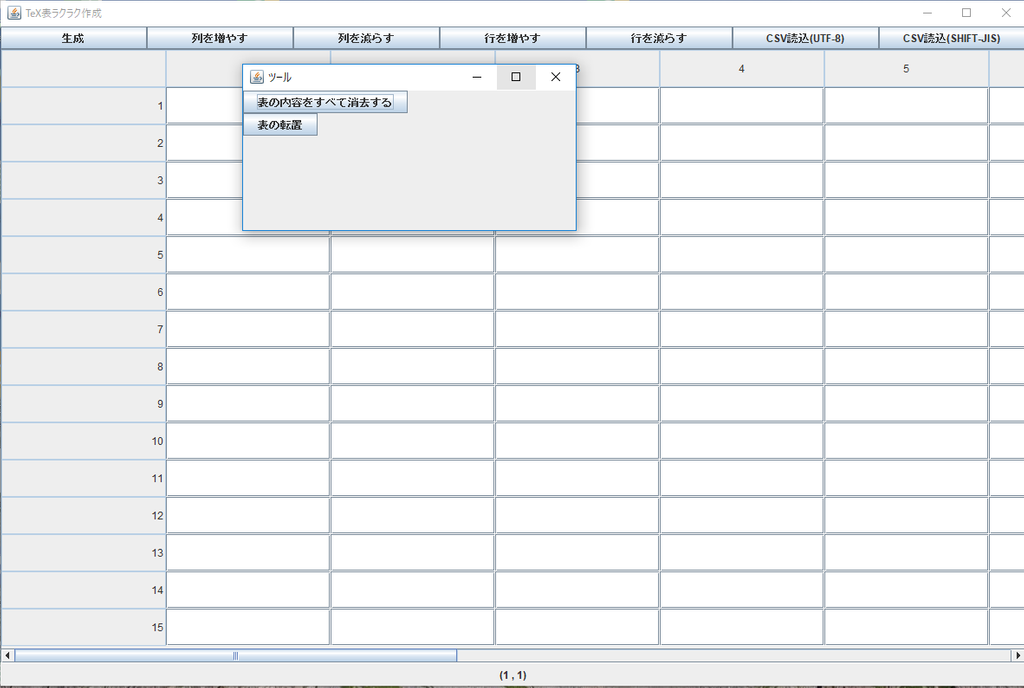
javaaa
操作方法はだいたいExcelに似せている（劣化）ので操作で困ることはないと思います（多分）。

よかったら使ってね（多分誰も使わない）
↓
GitHub

あとがき

ガバガバ説明すいません。
低クオリティーだ
最後まで読んでいただきありがとうございます。
技術アドバイスとしてsirodoni氏に感謝します。ありがとうございました。
どうでもいいけどOpferくんとぼくで2連続福岡県民が来て草

以上、18のKejunでした。

4/12はoribeさんです。楽しみ～

Kejun icon
この記事を書いた人
Kejun

福岡県民です。

この記事をシェア

このエントリーをはてなブックマークに追加
共有

関連する記事

2019年4月22日
アセンブリを読んでみよう【新歓ブログリレー2019 45日目】
eiya icon eiya
2019年4月16日
Logicのすヽめ+新歓コンピ宣伝
SolunaEureka icon SolunaEureka
2019年3月16日
競技プログラミングを始めよう【新歓ブログリレー2019 8日目】
eiya icon eiya
2019年4月12日
iPadでGitお絵かきをしよう！
oribe icon oribe
2019年3月20日
大富豪やろうぜ。【新歓ブログリレー2019 12日目】
iF icon iF
2019年4月24日
gnuplotで遊ぼう
mds_boy icon mds_boy
記事一覧 タグ一覧 Google アナリティクスについて