この記事はこの記事は新歓ブログリレー2024、52日目の記事です。
本記事では1, 2年生に向けて機械学習に関連する線形代数のトピック,特に主成分分析(PCA)に関連したトピックを紹介します。理論的なところから始め,最後にPythonで簡単な実装をしてみます。「線形代数学第二」(3Q or 4Qで履修) 程度の内容で1年生の線形代数のモチベーションになることを目標にして書きました。履修した2年生は難なく読めると思います。1年生は全部は読めないかもしれませんがぜひ眺めてみてください。線形代数学第一で僕を担当してくださった先生は以下で扱う線形代数のトピックを雑談で話されていて,その時に知っていればより面白かったのではとも思います。
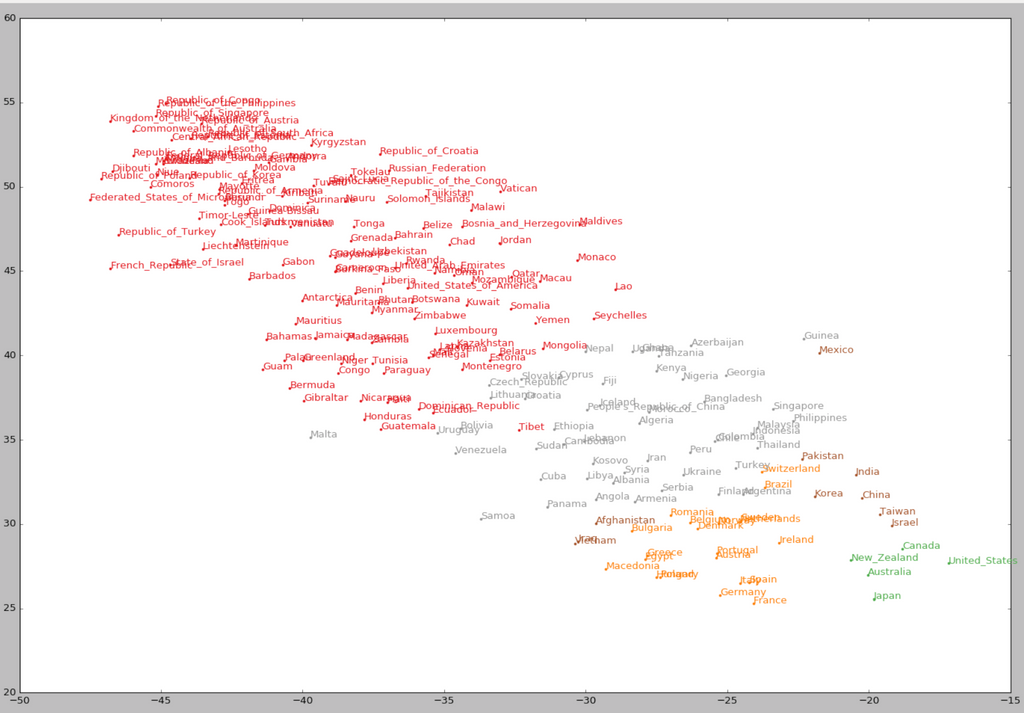
主成分分析はいわゆる流行りの人工知能と直接的な関わりはありません。しかし応用として,例えば単語ベクトルの可視化やオートエンコーダーなど最近のいわゆる人工知能の技術が挙げられます。単語は高次元のベクトルとして扱うことができて,意味の近さがベクトルとしての近さに反映されます。これを可視化したのが下図です。(位置ベクトルとして点で表されています。)2次元まで削減しているにも関わらず,関係性を保ったままほとんど重なることなく図示できています。関係性の例として,右下の日本を表す点はオーストラリアやアメリカ、カナダといった文化的に近い国を表す点の近くにありますね。
 |
|---|
(上図は[4]からの引用でt-SNEという手法を用いています。)
それでは実際に主成分分析の紹介に入っていきます。
射影行列
まず主成分分析の理論を説明するために便利な射影行列について解説します。
単位ベクトルの復習
単位ベクトルはとても便利な道具で,
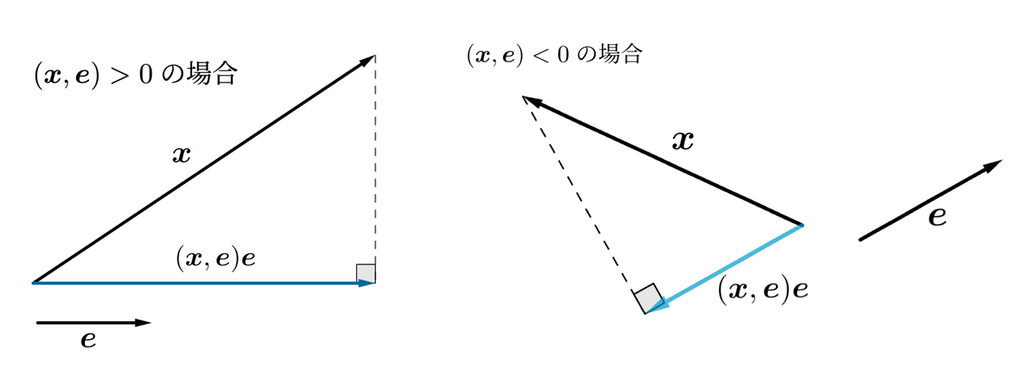
- 内積を取ることで単位ベクトルの方向成分の符号付きの長さを求められる。
- ベクトル(3, 5)と軸の単位ベクトル(1, 0)とで内積をとると軸方向成分である3が得られます。ただし負になることもあるので「符号付き」としました。
- で方向,符号付き長さのベクトルを作れる。
これらを用いると,正射影ベクトルがすぐ導けます。の方向の正射影ベクトルは
と書けます。ただし,は内積とします。
 |
|---|
射影する関数は線形性を持ちそうです。よって(標準基底を取って)行列として射影を関数を表せそうです。
線形性を持ちそうと言うのは,図形的に,ベクトルを定数倍してから射影しても射影してから定数倍しても等しそうで,和の射影と射影の和も等しそうということです。関数が線形性を持つとき行列で表すことができます。
実際,
(実数は の行列とみなしています。行列積は一般には可換ではないですが上であることは成分計算すれば分かります。)
となるのでと置くと,と書けます。 このは直交射影行列と呼ばれます。ここでは直交でない射影行列は扱わないので単に射影行列と書くことにします。ところで方向に,射影したものをもう一度射影しても変わりません。また式の形からして対称行列です。すなわち次が成り立ちます。
🐾 直交射影行列の性質
補足:こちらの2つを満たす行列を直交射影行列と定義する場合が多いです。本記事では直感的なわかりやすさのために逆側から紹介しています。
問題
とする。
- の張る空間(これは原点を通る直線)に射影する射影行列を求めてください。
答え
- の張る平面に射影する射影行列を求めてください。
ヒント: ベクトル の平面への正射影はどのように書けるでしょうか。
答え
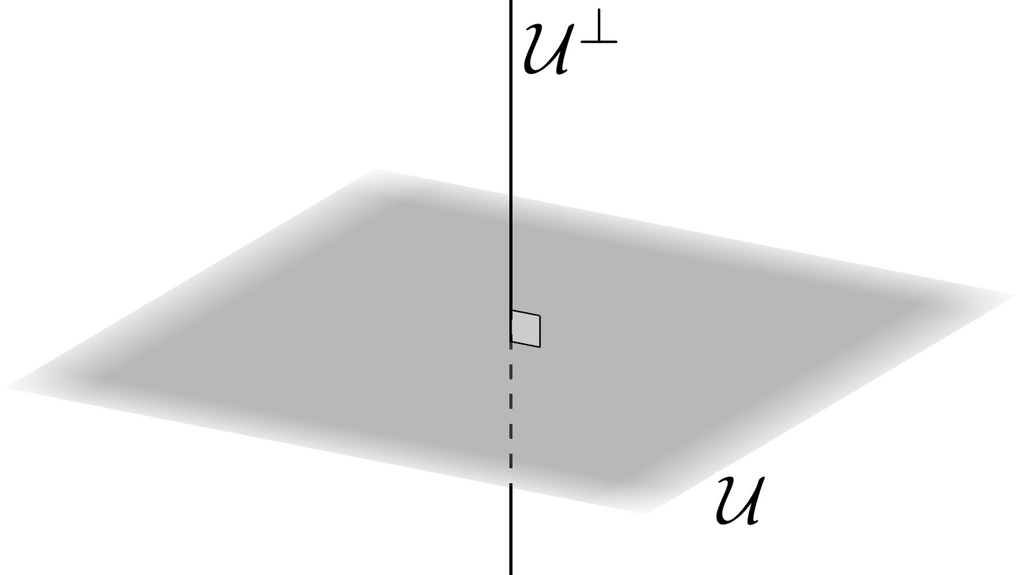
- はの正規直交基底です。の張る部分空間の直交補空間への射影行列を求めてください。
 |
|---|
答え
補足: への射影行列をと書くと, 答えはとも書けます。この式は機械学習でたまに見かけます。直交補空間への射影行列だったのですね。また,単位行列も射影行列です。
- を直交射影行列, とします。 と が直交することを示してください。
答え
確かに上の直交射影行列の性質を定義としても良さそうということがわかります。
主成分分析
主成分分析は機械学習の手法の一つで,簡単に言うと情報をなるべく減らさずにデータの次元を下げる手法です。
データのパラメータが大きいときに,それを可視化したり扱ったりするのは大変になりがちです。まず,少なくとも2~3次元まで落とさないと可視化は難しそうです。しかも,高次元での振る舞いは奇妙で1,000,000次元の単位超立方体で無作為に2つの点を選ぶとその平均距離は約408.25(3次元は約0.66)。 データの点同士がより離れているので低次元のときと比べて予測の信頼性が落ちてしまいます。
実際にどのように次元を落とすかですが,下の画像のデータは直線を当てはめて射影することで1次元に落とせそうです。
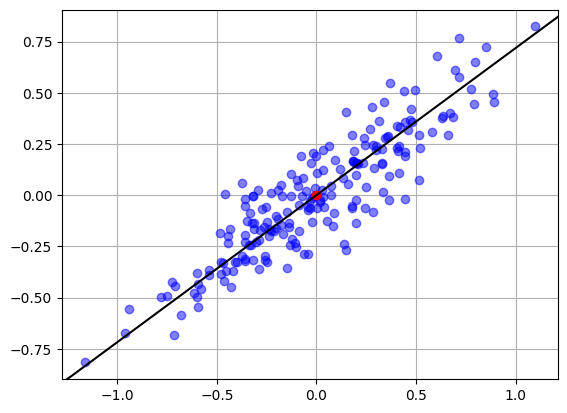
このように直線や平面の当てはめて射影して次元を下げるのが主成分分析です。
どのように当てはめるか 分散は情報の大きさ
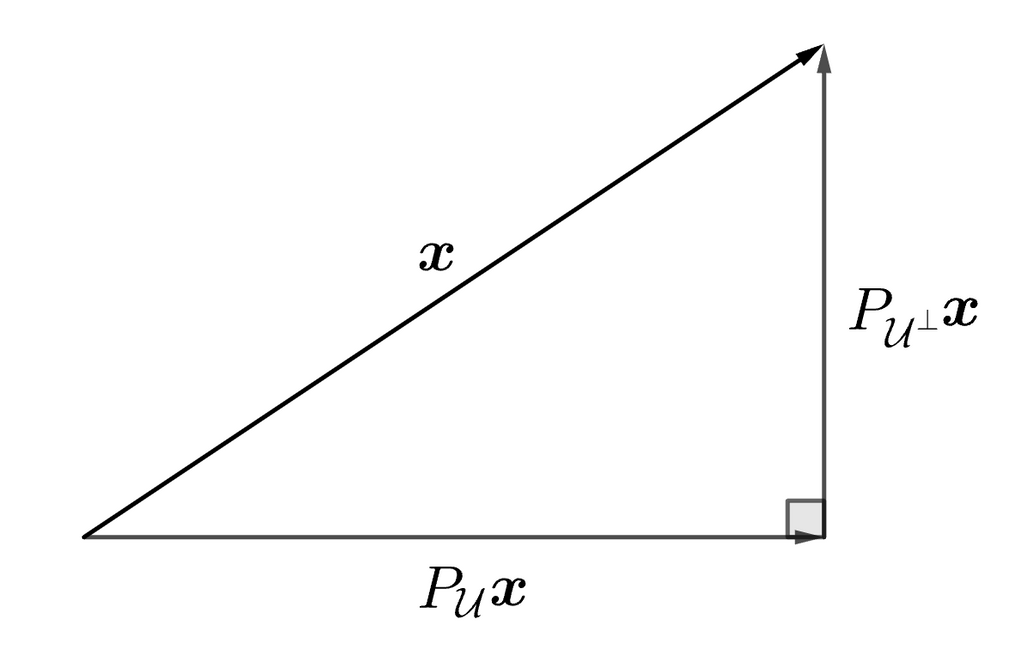
さてどのような指標を使って最もフィットする直線を決めれば良いでしょうか?結論としては主成分分析では射影行列を使って,ある直線に射影し,その射影と元のベクトルとの差の長さ()の2乗をデータ全体で和をとったものを最小化するような直線を求めます。
 |
|---|
それではベクトルを直線にあてはめるとき,なぜこのような指標で考えるのでしょうか?
それは分散が最も大きく維持される当てはめを見つけることができるからです。分散というのは情報の大きさと見ることができます。例えば,全人類に関する遺伝子のデータがあったときに染色体の本数という一次元の指標で射影してしまうと(つまり他のデータは無視してしまうと),確かに次元は下がりましたが,ほとんどの人類が46本のところに集中して(つまり分散が小さい)まるっきり情報がありません。というのは射影したデータはほとんど、ほとんどの点が46のところで重なってしまって、そこから有益な情報を得られそうにありません。例えば、どの点が日本人か?ということにも全くわからないでしょう。また,最頻値や平均値であろう46という数字がありさえすればよく,あえて分布として考える必要もありません。一方,身長や体重,年齢などそれなりにばらつき,分散が大きいので分布が意味を持ちます。(性別や国籍などを予測するモデルを作ることができるでしょう。)それではどのようにあてはめる直線を求めるのか見ていきましょう。
ここで,補足として,当てはめる直線や平面と述べてきましたが,正確にはアフィン空間の当てはめです。アフィン空間とは部分空間を並行移動したものです。例えば,原点を通らない直線も並行移動して原点を通るようにすると部分空間になるのでアフィン空間です。定義は以下で与えられますがこの記事では使いません。
アフィン空間の当てはめとは、通る一点と、そこを原点とみなしたときの部分空間の基底を求めるだけです。例えば,直線の当てはめであれば、通る1点と方向ベクトルを求めます。
定義:アフィン空間
アフィン空間(集合)とはの部分集合Vであって以下を満たすもの。
まず,求めるアフィン空間はデータの重心を通ることを示します。すなわち(の基底を固定したとき)では極小値を取ることを示します。
で張られる空間をとします。
射影行列の性質を使って
とおくと,
ところで一般にベクトル空間とその直交補空間に対して
であることが示せます。(やってみよう)
これらより,を満たすの値は全体で,のどの点をとっても同じですが(の基底が等しいため,例えばこの例では二つの平行な直線であるため)
例えばを取るとよっては重心を通ることが示されました。
どの点を取っても同じということについて:上の例だとという点を任意に取ると,
このときアフィン空間の定義からすなわちとなって結局重心は求めるアフィン空間に属するということです。
さて今度は基底を求めます。
まず,にを代入して中心化しておきます。これで当てはめるアフィン空間は原点を通ります。
三平方の定理より
三平方の定理という図形的考察に頼らなくとも前述の射影行列の性質を使うことでも求められます。(やってみよう)
一旦,分散のことは置いておいて,単に当てはめた直線と点の距離の2乗和の総和を小さくすることを考えてみます。これは化学や物理の実験で使う最小二乗法に似ていますが,最小二乗法は残差(予測値とデータの値の差)の2乗であって,当てはめた直線と点の距離の2乗ではないです。
は定数であるので,の最小化問題はの最大化問題に帰着されました。これについて次々節で詳しく見ていきます。
統計的な意味
はだったことを思い出すと,最大化したは射影したデータの分散のデータの個数倍と見れますね。分散の最大化をしていた訳です。
固有値と2次形式の最大最小
さて主成分分析の理論は結局,2次形式の最大値問題に帰着されました。
求めるは固有値を使うことで簡単に求めることができます。なお,このを第一主成分,方向の符号付きの長さを第1主成分スコアと呼び,に直交する平面でもう一度直線の当てはめを行って得られた主成分は第2主成分,その方向の符号付き長さは第二主成分スコアと呼ばれます。これは二つの直交する直線を当てはめているのでつまり平面の当てはめです。
高次元データでは第3主成分, 第4, 第5, ...と必要な分だけ増やしていきます。
定理 2次形式の最大最小
対称行列
の固有値を (だだしとする)
単位ベクトルに対する2次形式の最大値は, 最小値はである。
(証明)
対称行列の固有ベクトルは正規直交系をなす様に取ることができます。(対称行列について,異なる固有値に対応する固有ベクトルたちは互いに直交しているので正規化することで正規直交系とすることができる)
この正規直交系をなすベクトルをただし固有値がととが対応するとします。
(対称行列は固有ベクトルをただ個だけ持つ)
またたちは本の一次独立なベクトルなのでの正規直交基底です。
よって,任意に与えられた単位ベクトルをたちの線形結合で表すことができて,
これを代入して
最後はは単位ベクトルだからであることを用いました。
等号成立はのとき。
よって2次形式の最大値は.同様にして最小値は.
特異値分解
主成分分析ではの固有ベクトルを求めましたが,特異値分解という手法を用いると少ない計算量での固有ベクトルを求めることができます。
一般の行列について,
なる組は個だけ存在する。
をそれぞれ左特異ベクトル, 右特異ベクトルと呼び,左特異ベクトルはの固有ベクトルになっています。また,右特異ベクトルはの固有ベクトルで,は固有値の平方根になっています。(自分で確かめてみよう)
特異値分解をする方が対角化をするよりも一般に高速なので実際には特異値分解での固有ベクトルを求めます。
この特異値,特異ベクトルを用いると行列を次のように分解することができます。
を同じ順番に,
と並べて
と表せることを指すことが多い。(の定義にはいくつか流儀があるようですが,次の節のコラム考慮するなら上の定義のが良いと思う。)
次のようにも表せます。計算する際にはこちらのが便利です。
またこの記事ではと並び替えてあるとします。
補足: について
まずを示す。
任意にが与えられたとする。からとなって よって
任意にが与えられたとすると,
ここでよりすなわち
これより, よって
ここでは数ベクトルを扱っているので
次元定理より
よって
ところで右特異ベクトルはの固有ベクトルでした。(の固有ベクトルであることが必要。)次にの非負固有値の個数はに等しいことを示します。
は半正定値行列であることが示せます(略)
は対称行列なので直交行列で対角化可能で,つまり正規直交系をなす
を列ベクトルに持つで対角化できて,(ただし,固有値が降順になるようにたちをとります。)
に対して
と表せるのででない固有値の数とがちょうど等しいことがわかります。対応する固有値がでない固有ベクトルがの右特異ベクトルです。
半正定値行列だったのででない固有値は全て正です。よってとすれば良いですね。
最後に,右特異ベクトルと特異値から左特異ベクトルが得られます:
と定義すると特異値・特異ベクトルの定義を満たしていますね。
コラム ムーア・ペンローズ型の一般逆行列
逆行列は少なくとも正方行列でないと定義されませんでした。一般の行列に逆行列は定義されないのでしょうか?
ところで射影行列は射影した空間のベクトルに対しては単位行列のように働きます。
正方行列の逆行列とは
なるのことでした。
これを拡張し,に対し,
の列空間(を列ベクトルに分解した時,その列ベクトルの線型結合で張られる部分空間です)への射影行列を
とした時
なるをムーア・ペンローズ型の一般逆行列と呼びます。
ところでは実は左特異ベクトルの張る空間への射影行列と一致します。
簡単に説明すると,特異ベクトルは対称行列の固有ベクトルでもあったので正規直交系に選べます。
に対して
であり,は任意であるからです。
さて一般逆行列は次のよう定義されます。
は直交行列であることに注意すると,実際に,
途中で
を使いました。は列ベクトルなので自明ではありませんが成分計算で簡単に示せます。
この一般逆行列を用いて最小二乗法の解を直接書き下すことができます。また,最小二乗解を図形的に解釈すると射影を用いて直感的に捉えることが出来ます。
詳しくは参考文献[1]や関連するウェブサイトを探してみてください。
主成分分析って実際何をすればいいの
これまで理論よりに解説してきました。主成分分析をする手順を実際にまとめてみます。
-
縦ベクトルのデータを並べて行列を作ります。
-
を特異値分解し,左特異ベクトルを求めます。
-
第k主成分まで欲しい時は 対応する特異値が大きい順に左特異ベクトルを個とり並べて行列を作ります。
-
ベクトルの番目の成分が第主成分スコアになっています。まとめてデータ全体を射影するときはとすれば良い。
実践編
最後に簡単にPythonで主成分分析をしてみましょう。
まずは2次元のデータで行います。
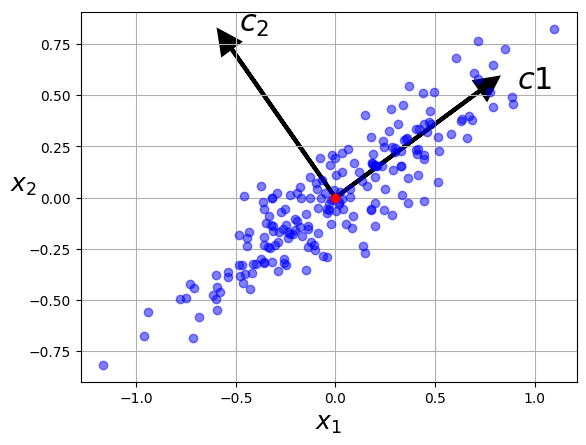
と書いてあるのが第1主成分のベクトルです。(は第2主成分のベクトル。データを方向に射影するよりも方向に射影する方が分散が保たれていますね。)
かなり人工的な設定ですが,標準正規分布に従う乱数を各要素にもつ行列を作り,最初は大体円形に分布しているのを軸方向に引き伸ばし回転させることで斜め楕円型の分布を得ます。上の理論パートの説明同様にの列ベクトルがデータの点です。
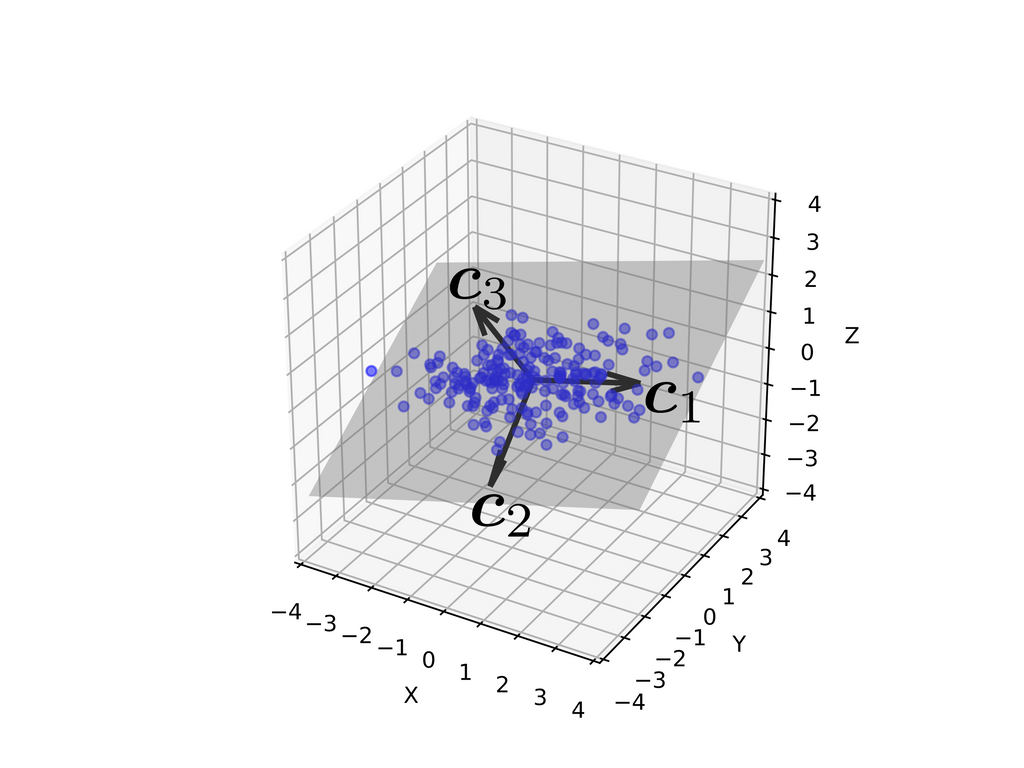
次に3次元のデータで主成分分析してみます。3次元から2次元に削減します。
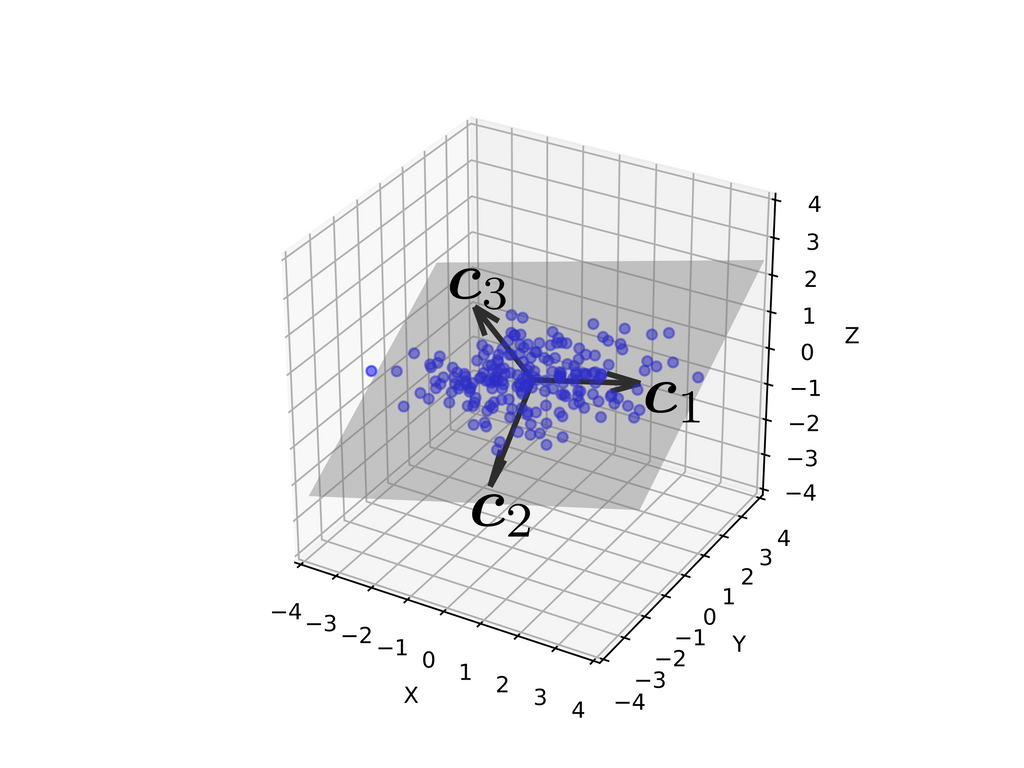
3本のベクトルが主成分です。が第主成分になっています。
第2主成分まで抽出する(灰色の平面に射影する)と次図のように情報を損なわずに次元が減らせていそうです。
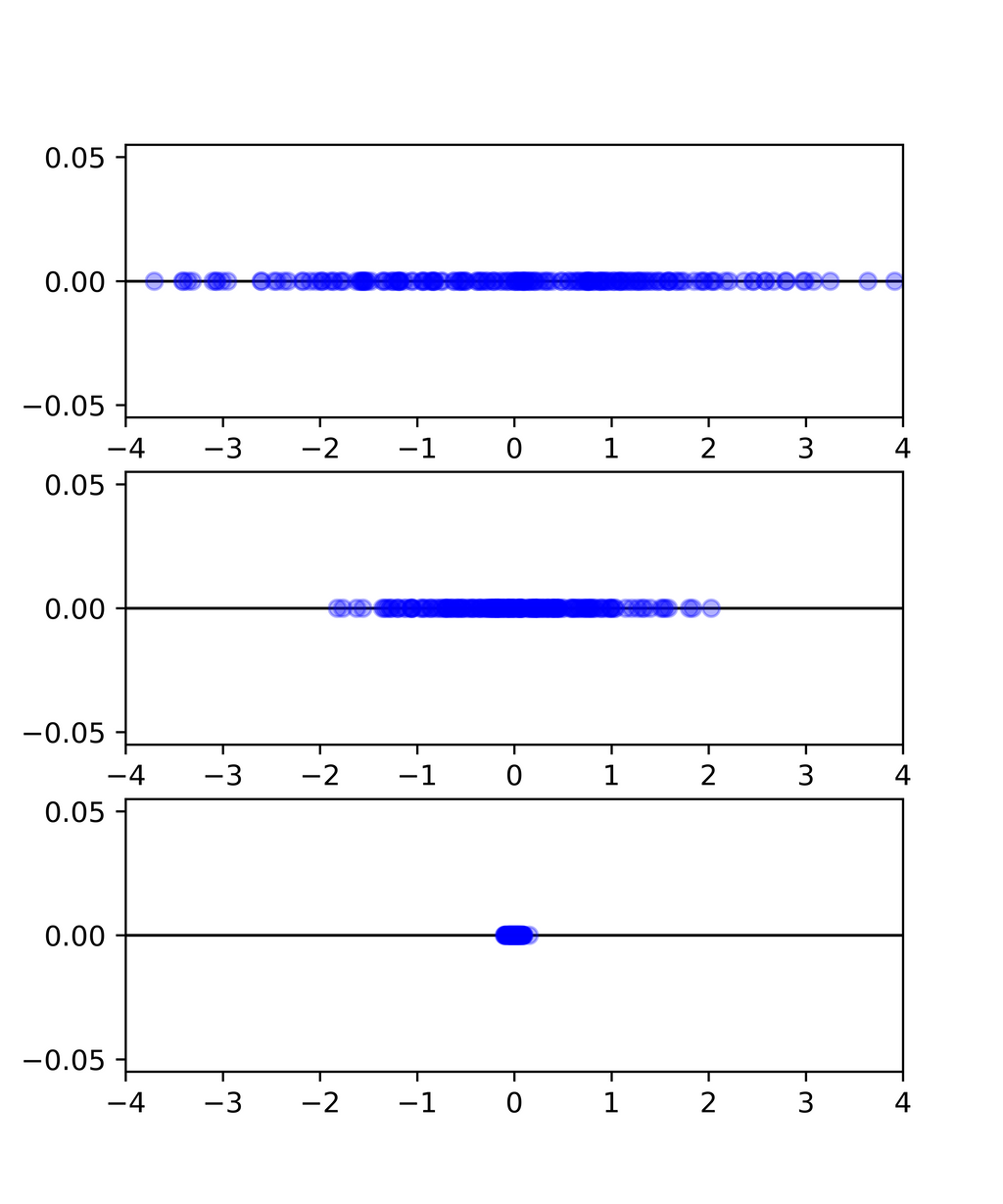
実際に各主成分の分布が次です。第1主成分スコアから第3主成分スコアに行くに従って分散が小さくなっています。
実際に何個主成分として取るかについて,ある主成分に射影したの分散は主成分に対応する固有値のに比例(データの個数に比例)するので,以下の累積寄与率をもとに何個目まで採用するかの基準にすることもできます。
第成分までの射影した値についての分散はであることを踏まえて,
Pythonのコードは
import numpy as np
import matplotlib.pyplot as plt
angle = np.pi / 5
stretch = 5
m = 200
np.random.seed(3)
X = np.random.randn(2, m) / 10
X = np.array([[stretch, 0],[0, 1]]) @ X # Xを伸縮
X = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]) @ X # Xを回転
X_g = np.mean(X, axis=1) # 重心
# センタリング。 ブロードキャストの都合で転置同士で計算してさらに転置を取っているが
# 気持ちは X_centered = X - X_g
X_centered = (X.T - X_g.T).T
U, s, Vt = np.linalg.svd(X_centered) # 特異値分解
u1, u2 = -U[:, 0], U[:, 1]# 直線の基底なのでどちらを向いていても良い
plt.plot(X_centered[0, :], X_centered[1, :], "bo", alpha=0.7)
plt.plot(0, 0, "o", color="red")
plt.arrow(0, 0, u1[0], u1[1], head_width=0.1, linewidth=3, length_includes_head=True, head_length=0.1, fc='k', ec='k')
plt.arrow(0, 0, u2[0], u2[1], head_width=0.1, linewidth=3, length_includes_head=True, head_length=0.1, fc='k', ec='k')
plt.text(u1[0] + 0.1, u1[1] - 0.05, r"$c1$", fontsize=22)
plt.text(u2[0] + 0.1, u2[1], r"$c_2$", fontsize=22)
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$x_2$", fontsize=18, rotation=0)
plt.grid(True)
plt.show()
3次元版
import numpy as np
import matplotlib.pyplot as plt
angle1 = np.pi / 6
angle2 = -np.pi / 12
stretch1 = 25
stretch2 = 10
m = 200
np.random.seed(3)
X = np.random.randn(3, m) / 15
X = np.array([[stretch1, 0, 0],
[0, stretch2, 0],
[0, 0, 1]]) @ X # 伸縮
X = np.array([[1, 0, 0],
[0, np.cos(angle1), -np.sin(angle1)],
[0, np.sin(angle1), np.sin(angle1)]]) @ X # x軸周りに回転
X = np.array([[np.cos(angle2), 0, np.sin(angle2)],
[0, 1, 0],
[-np.sin(angle2), 0, np.cos(angle2)]]) @ X # y軸周りに回転
X_g = np.mean(X, axis=1) # 重心
# センタリング。 ブロードキャストの都合で転置同士で計算してさらに転置を取っているが
# 気持ちは X_centered = X - X_g
X_centered = (X.T - X_g.T).T
U, s, Vt = np.linalg.svd(X_centered)
# 左特異ベクトルを抽出
u1 = -U[:, 0] # 逆を向いていても良い。図の見やすさのために逆にする。
u2 = U[:, 1]
u3 = U[:, 2]
normal_vector = np.cross(u1, u2) # 平面の点を得るために使う
xmin,xmax=-4.0, 4.0
ymin,ymax=xmin,xmax
zmin,zmax=xmin,xmax
x = np.linspace(xmin - 0.5, xmax + 0.5, 1000)
y = np.linspace(ymin + 1.0, ymax - 1.0, 1000)
xx, yy = np.meshgrid(x, y)
zz = - 1 / normal_vector[2] * (normal_vector[0] * xx + normal_vector[1] * yy)
fig = plt.figure()
ax = fig.add_subplot(projection='3d', aspect='equal')
ax.set_xlim3d(xmin, xmax)
ax.set_ylim3d(ymin, ymax)
ax.set_zlim3d(zmin, zmax)
ax.plot_surface(xx, yy, zz, color="gray", alpha=0.4)
ax.scatter(X[0, :], X[1, :], X[2, :], color="blue", alpha = 0.5)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
# 主成分の軸の描画
ax.quiver(*[0, 0, 0], *u1, color="black", length=3, linewidth=2.5)
ax.quiver(*[0, 0, 0], *u2, color="black", length=3, linewidth=2.5)
ax.quiver(*[0, 0, 0], *u3, color="black", length=3, linewidth=2.5)
plt.savefig("01.png", format="png", dpi=800)
# 第1, 2主成分をプロット
A = U.T
X_proj = A @ X_centered
plt.figure()
plt.plot(X_proj[0, :], X_proj[1, :], "bo")
plt.savefig("02.png", format="png", dpi=800)
# 各主成分の分布
xmin2, xmax2 = -4, 4
fig = plt.figure(figsize=(5, 6))
ax1 = fig.add_subplot(3, 1, 1)
plt.xlim(xmin2, xmax2)
ax1.plot([-4, 4], [0, 0], "k-", linewidth=1)
ax1.plot(X_proj[0, :], np.zeros(m), "bo", alpha=0.3)
ax2 = fig.add_subplot(3, 1, 2)
plt.xlim(xmin2, xmax2)
ax2.plot([-4, 4], [0, 0], "k-", linewidth=1)
ax2.plot(X_proj[1, :], np.zeros(m), "bo", alpha=0.3)
ax3 = fig.add_subplot(3, 1, 3)
plt.xlim(xmin2, xmax2)
ax3.plot([-4, 4], [0, 0], "k-", linewidth=1)
ax3.plot(X_proj[2, :], np.zeros(m), "bo", alpha=0.3)
plt.savefig("03.png", format="png", dpi=800)
補足:
本記事では[1]に合わせてデータ点を列ベクトルとして横に並べて行列を作りましたが、[3]をはじめとして転置したものをとすることも多いです。また後者の方がPythonで書く際にブロードキャストが使える範囲が広く便利です。
参考文献
線形代数は以下2冊の本,特に前者の本を参考にしました。
[1]『線形代数セミナー』https://www.kyoritsu-pub.co.jp/book/b10003952.html
[2]『これならわかる深層学習入門』https://www.kspub.co.jp/book/detail/1538283.html
実装例はこの本を参考にしました。
[3]『scikit-learn,Keras,TensorFlowによる実践機械学習 第2版』https://www.oreilly.co.jp/books/9784873119281/
t-SNEの例はこちらからの引用です。
[4] https://qiita.com/segavvy/items/fe530927df30732e2a46
[5] 機械学習練習帳
https://chokkan.github.io/mlnote/unsupervised/03pca.html
情報工学系では機械学習という授業で主成分分析を扱います。その講義資料です。
固有顔のような例が述べられています。
次は統計について書こうかな