この記事は2023夏ブログリレー28日目の記事になります。

はじめに

こんにちは。koukawa_ppです。
本日は2023年9月18日です。あの大数学者レオンハルト・オイラーが亡くなって240年になります。
彼は一人の人としては信じられないほどのたくさんの成果を残したことで大変有名で、たとえばベタですが僕の好きな式の一つである

$$e^{i\pi }=-1$$

という式は、オイラーの証明した公式である

$$e^{iz}=\cos z+i\sin z$$

に $z=\pi$ を代入することで得ることができます。

さて、皆さんは $\pi$ はお好きでしょうか？
$\pi$ はふつう円周率と呼ばれ、ある円について、円周の長さを直径で割ったものとして定義されます。
これは算数や数学の中でも最も有名な定数と言っても過言ではないでしょう。

$$\pi =3.141592653589793238462643\cdots$$

と続いていきます。

さて、小数点以下に数字が無限に続くような数を無理数と言いますが、円周率も無理数です。
そして人は分からないものを調べてでも知りたくなる生き物です。
これにより、人は昔から、円周率の小数点以下の数字を求めることに躍起になってきました。

今回は、そんな先人たちの苦労を（ソフトな形で）経験するために、いろいろなPythonプログラムやシミュレーションを通して、円周率を実際に計算してみましょう。

なお、こちらのページで公開しているプログラムは、全てMITライセンスの下での扱いを許諾いたします。

Copyright (c) 2023 koukawa_pp
Released under the MIT license
https://opensource.org/license/mit/

直接的に求めてみ（ようとす）る

一番簡単に思いつく方法としては、ある直径の円の円周の長さを測り、その値を直径で割るという方法です。一番単純に考えれば、直径が1の円の長さの円周の長さは円周率になります。
ただし、これには限界があることが分かります。なぜなら、測定できる長さの精度に限界があるからです。直径の長さを大きくすればその分どうにかなりますが、延々と伸ばし続けるわけにはいきません。
また物理的に測定するとしても、曲線の長さを正確に測定できる定規といったものは（少なくとも僕の身近には）ありません。
それゆえ、この方法で円周率を測定するのはちょっと難しいです。

確率を使って求める（モンテカルロ法）

ここからは、長さを測らずに円周率を求める方法を紹介します。
有名な方法の一つに、「モンテカルロ法」というものがあります。

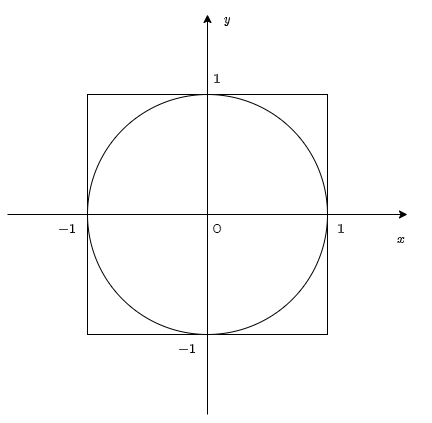
上図のように、一辺の長さが2の正方形と、そこに内接する円を考えます。
そして、この正方形の中に一定数の点を打ち、円の中に入った点の数を数えることにより、円周率を求めます。

どうやって求められるのか？ということですが、これは確率を利用します。
正方形の面積は4であり、円の面積は、円の半径が1であることから、$\pi$ です。
そして点が正方形の中に打たれるとき、この点の位置の決まり方がランダムな場合、正方形の面積が4, 円の面積が $\pi$ であること、または正方形の中に点が打たれる確率は1であるので、円の中に点が打たれる確率を $x$ とすると、

$$4:\pi =1:x$$

が成り立ちます。これより、正方形の中にランダムに点を打つとき、円の中に点が打たれる確率は、$\frac{\pi }{4}$ とできます。
そして、正方形の中に打った点の個数で、円の中に入った点の個数を割れば、円の中に点が打たれる確率を求めることができるため、これより、円周率を求めることができます。

では、プログラムを使ってどうやって求めるか考えましょう。
一番簡単な方法は、先ほどの図に座標を導入することです。

先ほど、正方形の一辺の長さは2だと言いました。
それゆえ、正方形の中心を原点とすれば、正方形と$x$軸、$y$軸の交点はそれぞれ $(-1,0),(1,0)$ と、$(0,-1),(0,1)$ とできます。
ここから、求めるのは、$x$ 座標を-1以上1以下で、$y$ 座標も-1以上1以下でランダムに選び、それが半径1の円内、すなわち単位円内に存在している点の個数を調べるということです。

さて、単位円の方程式は、$x^2+y^2=1$ になります。ですから、この内部にある点となると、その座標 $(x,y)$ は、$x^2+y^2\leqq 1$ を満たします。すなわち、ここで生成した乱数の2乗和が1以下であれば、円内に点が打たれたと見なすことができます。

これらのことをプログラムにすると、以下のようになります。

calc_pi_monte_carlo.pyimport random

num_points = 10000000
num_in_points = 0

for _ in range(num_points):
    x = random.random() * 2 - 1
    y = random.random() * 2 - 1

    if x * x + y * y <= 1:
        num_in_points += 1

print("pi: {}".format(num_in_points / num_points * 4))

下からもダウンロードできます。よろしければどうぞ。

少しプログラムの説明をします。
まず、num_pointsで、正方形内に打つ点の個数を決めます。
10000000だとちょっと実行するのに時間が掛かります。（待てない時間ではないです。）
次に、num_in_pointsは、円内に打たれた点の数を数えるカウンタです。

そのあとはforループによって、num_points回点を打つ試行を行っています。
ここでは、x および y にrandom.random() * 2 - 1 を代入しています。
random.random() は、0以上1未満の小数乱数を発生させる関数で、この乱数を-1以上1未満にするために、少し式を書いています。
まず* 2により、この乱数を2倍しています。これをすることにより、発生する乱数は0以上2未満の小数になります。
ここから- 1をすることにより、発生する乱数が-1以上1未満になるという寸法です。

その後は、x * x + y * y <= 1 を求めることにより、これがTrueならnum_in_pointsを1増やしています。$x$ の2乗は $x\times x$ で求められますから、こうしています。
また、a <= b は、aがb以下であるかを表しています。

最後は、num_in_pointsをnum_pointsで割って、それに4を掛けた値を出力しています。
点が円内に入る確率は $\frac{\pi }{4}$ でしたから、最後は4を掛けないといけないですよね。

さて、このプログラムを10回ほど繰り返すと、以下のような出力を得ました。

pi: 3.1416764
pi: 3.141472
pi: 3.1408152
pi: 3.140804
pi: 3.1411432
pi: 3.1418784
pi: 3.14237
pi: 3.1427404
pi: 3.1421584
pi: 3.1411372

本来の値は $3.1415\cdots$ なので、かなりいい値が出ているのではないでしょうか。

モンテカルロ法を試してみる

実際にモンテカルロ法をシミュレーションできるHTMLをご用意しました。よろしければお試しください。
大きい数字を入れると結果がすぐに出てこない場合があります。また、上限値を10000000としています。
（1000~100000程度がお勧めです。）

計算で求める（その1：ライプニッツの公式）

上の方法は面白い方法です。確率的に考えればもちろんそうだよな、といったそんなところです。
しかし、世の中疑似乱数がそこまで精度の良いものばかりというわけではありません。
Pythonはメルセンヌ・ツイスタという精度のよい疑似乱数生成アルゴリズムを採用していたので、精度的な意味ではそこまで差支えがあるわけではありませんが、完璧な乱数は（今のところは、そしてしばらくは）ありえないので、たくさん点を打てば打つほどその綻びが出てしまいます。

もう一つこの方法には大きな欠点があります。モンテカルロ法で円周率を求める方法が、整数を整数で割ることにあります。つまり、より細かい値を求めて精度をよくするには、割る数を大きくしなければならないという欠点があるのです。最後は結局4を掛けていたので、例えば割る数（打つ点の数）を10000000にしたとしても、実質2500000で割っていることと同じなので、もし打つ点の数を40000000というとても大きな数にしたとしても、実質計算結果は高々小数点以下7桁しか出てこないのです。

以上のことから、計算でより精度よく求められる方法があるなら、そちらの方が確実であるはずです。
色々探してみると、円周率を使った値に収束する級数が多くあることが分かります。
その一つに、ライプニッツの公式というものが挙げられます。

ライプニッツの公式とは？

ライプニッツの公式とは、以下のようなものです。

$$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

なぜこんな式で表すことができるのか？ということについては、少し今回のお話の本筋と逸れるので、付録という形でこの記事の最後の方の章に載せておきます。

ライプニッツの公式は、上記の通り、無限級数です。
つまり、規則的に上の数字を足し合わせ続ければ、近似値が得られるというわけです。
やってみましょう。

ここでも一旦Pythonを使ってプログラムします。

calc_pi_leibniz.pyfrom fractions import Fraction

max_val = 500000

array = [Fraction(1, 2 * i + 1) if i % 2 == 0 else Fraction(-1, 2 * i + 1) for i in range(max_val + 1)]
res = sum(array)
print(float(res) * 4)

下からもダウンロードできます。よろしければどうぞ。

やっていることをお伝えします。
まず、最初はリスト内包表記を用いてarrayを初期化しています。iを0以上max_val以下で動かします。
そして、分母が2 * i + 1で、分子はiが偶数のとき1, 奇数のとき-1である分数をarrayに追加しています。これにより、arrayは、

$$1,\frac{-1}{3},\frac{1}{5},\frac{-1}{7},\cdots$$

が追加されることが分かります。

あとはこのリスト内の要素について総和を取ればいいわけです。
ここでは、Pythonの組み込み関数であるsum関数を使っています。
この総和は $\frac{\pi }{4}$ に等しいはずなので、結果は先ほどの総和に4を掛けたものになります。

実際にこれで動かしてみると、時間は多少かかりますが、

3.141594653585793

と出てきます。3.14159までは合っていますね。

ライプニッツの公式を試してみる

実際にライプニッツの公式をシミュレーションできるHTMLをご用意しました。もしよろしければお試しください。
なお、上限値を1000000にしています。

こちらのHTMLに埋め込まれているJavaScriptは、一部TypeScriptをビルドしたものを利用しています。
そのTypeScriptは下からダウンロードできます。

計算して求める（その2：マチンの公式）

先ほどの方法は確かに求められます。
ただ、ライプニッツの公式をいろいろ調べてみると、こんな言葉を見たことはありませんか？
「マチンの公式の方がより早く収束します」と。
こうなると、マチンの公式をいろいろ調べてみたくなりますよね。

マチンの公式は、以下のように与えられます。

$$\frac{\pi }{4}=4\arctan \frac{1}{5}-\arctan \frac{1}{239}$$

ここで、$\arctan x$ とは逆正接関数、すなわち $\tan x$ の逆関数です。
どうやったらこんな式が出てくるんでしょうか。それは謎ですが、これが正しいことは示すことができます。
こちらのページがマチンの公式のWikipediaです。ここに加法定理や二倍角の公式を用いたマチンの公式の証明があります。よろしければ参照ください。

この式を変形すれば、

$$\pi =16\arctan \frac{1}{5}-4\arctan \frac{1}{239}$$

とできます。これを使えばもちろん $\pi$ を求められますが、どうやって $\arctan$ を求めたらよいでしょうか。

ここでは、マクローリン展開というものを用います。
付録1でも実は説明させていただいたのですが、ここでも一旦お示しします。
マクローリン展開を用いて $\arctan$ を展開すると、以下のようになります。

$$\arctan x=x-\frac{1}{3}{x}^3+\frac{1}{5}{x}^5-\frac{1}{7}{x}^7+\cdots =\sum _{n=0}^{\infty }\frac{(-1{)}^n}{2n+1}{x}^{2n+1}$$

この導出は、付録1をご覧ください。

さて、これを使ってマチンの公式を表すと、以下のようになります。

$$\pi =16\sum _{n=0}^{\infty }\frac{(-1{)}^n}{2n+1}{\left(\frac{1}{5}\right)}^{2n+1}-4\sum _{n=0}^{\infty }\frac{(-1{)}^n}{2n+1}{\left(\frac{1}{239}\right)}^{2n+1}$$

あとはいくつまで $n$ を足し合わせるかということがポイントです。
ここで、$\frac{1}{5}$ の方と、$\frac{1}{239}$ の方について、足す項の数は異なってても良い、例えば $\frac{1}{5}$ の方は $n=30$ まで足して、$\frac{1}{239}$ の方は $n=10$ まで足すといったようなことも良いということです。
マチンの公式のWikipediaによれば、$\frac{1}{5}$ と $\frac{1}{239}$ の項数は、3:1の割合で足し合わせているようですが、これが本当に最善なのかも、プログラムを回すことで確かめてみましょう。

とりあえずPythonのプログラムを載せておきます。

calc_pi_machin.pyfrom fractions import Fraction

n1 = 100
n2 = 100

array1 = [Fraction((-1) ** n, (2 * n + 1) * 5 ** (2 * n + 1)) for n in range(n1)]
array2 = [Fraction((-1) ** n, (2 * n + 1) * 239 ** (2 * n + 1)) for n in range(n2)]
sum1 = sum(array1)
sum2 = sum(array2)
print("result: {}".format(float(16 * sum1 - 4 * sum2)))

ここからは、このプログラムにおいて、n1 と n2 の値をいろいろ変えて、結果を確認してみましょう。

まず、n1 と n2 をそれぞれ 100000 にした結果、プログラムの実行時間があまりにもかかり過ぎたので諦めました。
そこで、n1 と n2 をそれぞれ 1000 にした結果、プログラムの出力は以下のようになりました。

result: 3.141592653589793

これは、実は全て合っています。待てる時間でさえ、正確な結果を出してくれて、さらに出力できる桁数を溢れてしまったというのは、実に驚きなことです。

他の割合ではどうでしょうか。
n1 を500, n2 を1500にすると、以下のようになりました。

result: 3.141592653589793

これも完全に一致しています。

n1 を1500, n2 を500にしてみました。すると、

result: 3.141592653589793

これもまた完全に一致しています。
どうも n1 と n2 の合計を2000にすると、たいてい揃ってしまうようです。

n1 と n2 の合計が200でも、上記の通り全ての result が等しくなりました。
そこで、n1 と n2 の合計を20にしてみます。

まずは n1 と n2 をそれぞれ10にしてみます。すると、

result: 3.141592653589792

最後の桁だけが不一致のようです。

次に、n1 を15, n2 を5にしてみます。つまり、Wikipediaと同じような割合です。すると、

result: 3.141592653589793

全ての桁が一致しました。やはりこちらの方が正確です。

次に、n1 を5, n2 を15にしてみます。すると、

result: 3.1415926824043994

そうすると、3.1415926 までしか一致していません。やはりWikipediaが示していた足し合わせの項数の割合は侮れなかったようです。

ところで、実行可能な時間でプログラムを実行したとき、合っている桁数はすでに小数点以下15桁に及んでいることが明らかになりました。
そうなると、小数点以下16桁以上の数字を見たくなります。
それゆえ、ここで小数点以下16桁以上の値を求められるような関数を作ることにします。

calc_pi_machin.pydef frac_to_str(value: Fraction, index: int = 20) -> str:
    assert index > 0, "index must be positive."

    v1 = str(numerator // denominator)

    value = numerator % denominator
    v2 = ""
    while index > 4000:
        value *= 10 ** 4000
        v2 += str(value // denominator).zfill(4000)
        index -= 4000
        value %= denominator
    v2 += str(value * 10 ** index // denominator).zfill(index)
    return "{}.{}".format(v1, v2)

この関数は、value に与えられた分数について、小数点以下 index 桁まで小数として表示する関数です。
結果の整数部分は、numerator を denominator で割った商を求めればよいので、numerator // denominator で求められます。
小数部分については、以下のように求めています。

1. numerator を denominator で割った余りを求める。
2. 余りに、10を index 乗した数を掛ける。
3. 2. の数を denominator で割った商を求める。これを小数点以下の値とする。

この一連の操作を、4000文字ずつ行っています。
なぜ4000文字ずつであるかの理由はPythonの仕様によるもので、こちらのページが公式の発表だと思われますが、Pythonはセキュリティの観点から、一度に大量の文字の変換を行わないようになったことに起因しています。これにより一度におよそ4000文字強の数字をstr型に変換するとエラーが生じるようになったため、ここでは4000文字ずつに区切って操作を行っています。

この関数を組み込んだ結果、プログラムは以下のようになります。

calc_pi_machin.pyfrom fractions import Fraction

def frac_to_str(value: Fraction, index: int = 20) -> str:
    assert index > 0, "index must be positive."

    numerator: int = value.numerator
    denominator: int = value.denominator

    v1 = str(numerator // denominator).zfill(4000)

    value = numerator % denominator
    v2 = ""
    while index > 4000:
        value *= 10 ** 4000
        v2 += str(value // denominator)
        index -= 4000
        value %= denominator
    v2 += str(value * 10 ** index // denominator).zfill(index)
    return "{}.{}".format(v1, v2)

n1 = 100
n2 = 100

array1 = [Fraction((-1) ** n, (2 * n + 1) * 5 ** (2 * n + 1)) for n in range(n1)]
array2 = [Fraction((-1) ** n, (2 * n + 1) * 239 ** (2 * n + 1)) for n in range(n2)]
sum1 = sum(array1)
sum2 = sum(array2)
print("result: {}".format(frac_to_str(16 * sum1 - 4 * sum2)))

下からもダウンロードできます。よろしければどうぞ。

先ほどの実験で、先ほどの条件の中ではやはり n1 と n2 の比は3:1がよいということが分かったので、この比を使って計算していきましょう。
まず、n1 を3000, n2 を1000にして、frac_to_str の index を50にすると、結果は次のようになりました。

result: 3.14159265358979323846264338327950288419716939937510

どうも50桁でも全部合っているみたいです。

index を100にして実行し直すと、次のようになりました。

result: 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

これも全部あっているみたいです。

結局いろいろ index を変更して実行してみると、小数点以下4294桁まで一致していたことが分かりました。

次に、n1 を9000, n2 を3000にして、frac_to_str の index をいろいろ変更して実行してみると、これは正しい値と小数点以下12584桁まで一致しました。非常に優秀です。
少なくともライプニッツの公式を用いた場合より、かなり速く収束していることが分かります。

マチンの公式を試してみる

実際にマチンの公式をシミュレーションできるHTMLを埋め込みました。
もしよろしければお試しください。
下のボタンから、設定したい n1 と n2 の値を選択ください。

計算して求めてみる（その3：ラマヌジャンの公式）

さて、先ほどの式はすごい速さで収束しました。
しかし、「なんでそれで求められるのか？」となる式も一定数存在して、しかもその収束が速いという式もまた一定数あります。その一つとして、シュリニヴァーサ・ラマヌジャンの発見した式があります。

このような式です。

$$\frac{1}{\pi }=\frac{2\sqrt{2}}{99^2}\sum _{n=0}^{\infty }\frac{(4n)!(1103+26390n)}{(4^{n}99^{n}n!{)}^4}$$

一体何を食べたらこんな式が出てくるんでしょうかね。

とりあえず、これはその後正しい式であることは証明されました。
その証明は省略しますが（というか理解できる気がしませんが）、興味がありましたら調べてみてください。

この式がなぜ成り立つのかはとりあえず置いておいて、計算方法は多分高校数学で網羅可能かと思います。
階乗、平方根、無限級数と、これまで習ってきたことが詰め込まれているものだと思います。
今回はこれをPythonを使ってプログラムしようと思います。

$\sqrt{2}$ をどうやって求める？

ではまず、$\sqrt{2}$ をどうやって求めるかを考えましょう。

一番シンプルな方法は、Pythonの組み込み関数を使う方法です。

sqrt2 = math.sqrt(2)

こうすると、出力は以下のようになります。

1.4142135623730951

しかし、この方法には致命的な問題があります。というのも、これは正確な円周率の値を求めるのが目的だからです。つまり、小数点以下16桁のみを使うと、その分だけ最終的な結果の誤差が大きくなってしまう可能性が考えられるということです。今回は、$\sqrt{2}$ のなるべく正確な値を求めておいた方が、後々確かな値を出すことができるはずです。

では、どうやって $\sqrt{2}$ の正確な値を求めるかを考える必要があります。
今回は、「ニュートン法」というものを用いて求めようと思います。

ニュートン法の主張は、

$$a_{n+1}=\frac{1}{2}\left(a_n+\frac{2}{a_n}\right),a_1>0$$

で定義される数列 $a_n$ について、

$$\sqrt{2}=\underset{n\to \infty }{\lim }{a}_n$$

であるというものです。

正確には、ニュートン法は $\sqrt{2}$ の値を求めることしかできないわけではなく、もっと汎用性のあるアルゴリズムです。
この手法の詳しいことについては、付録でご説明しますので、当記事の最後の方をご覧ください。

さて、これをプログラムにすると、以下のようにできます。

calc_sqrt2_newton.pyfrom fractions import Fraction

def frac_to_str(value: Fraction, index: int = 20) -> str:
    assert index > 0, "index must be positive."

    numerator: int = value.numerator
    denominator: int = value.denominator

    v1 = str(numerator // denominator)

    value = numerator % denominator
    v2 = ""
    while index > 4000:
        value *= 10 ** 4000
        v2 += str(value // denominator).zfill(4000)
        index -= 4000
        value %= denominator
    v2 += str(value * 10 ** index // denominator).zfill(index)
    return "{}.{}".format(v1, v2)

def calc_better_sqrt2(acc: int = 10) -> Fraction:
    a = Fraction(1)
    
    for _ in range(acc):
        a = (a + 2 / a) / 2
    
    return a

a = calc_better_sqrt2()
print(frac_to_str(a * a, 500))

これを実行すると、以下のような出力を得られます。

2.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

つまり、これで得られた結果の2乗は、小数点以下500桁がすべて0になるということが分かります。
かなり精度は良いのではないでしょうか。

ちなみに、Pythonの標準ライブラリ math の関数である math.sqrt について、以下のようなプログラムを組むと、

import math
a = math.sqrt(2)
print(a * a)

出力は以下のようになりました。

2.0000000000000004

この桁でもなお誤差が出てしまいます。
そう考えると、先ほどのニュートン法の結果は相当優秀だと分かるのではないでしょうか。

ニュートン法を試してみる

実際にニュートン法をシミュレーションできるHTMLを埋め込みました。
初期値を下のラジオボタン（1, 3, 4, 5）から選択して、お試しください。
こちらでは、ニュートン法を1~10回やったときの結果の移り変わりを示しています。

なぜ初期値に2が無いのか？ということですが、これは実際に先ほどの漸化式

$$a_{n+1}=\frac{1}{2}\left(a_n+\frac{2}{a_n}\right)$$

に $a_1=1$ または $a_1=2$ を代入してみれば分かります。

たとえば $a_1=1$ を代入すると、

$$a_2=\frac{1}{2}\left(1+\frac{2}{1}\right)=\frac{1}{2}(1+2)=\frac{3}{2}$$

となります。

次に $a_1=2$ を代入すると、

$$a_2=\frac{1}{2}\left(2+\frac{2}{2}\right)=\frac{1}{2}(2+1)=\frac{3}{2}$$

となります。

これより、$n\geqq 2$ においては、$a_n$ は $a_1=1$ の場合と $a_1=2$ で等しくなるので、結局初期値($a_1$)に1を設定することと2を設定することが同じになるわけです。

円周率を計算していく

これを使ってラマヌジャンの公式を計算してみようと思います。
今回は有理数で近似値を出しているので、分数で計算するラマヌジャンの公式とは相性抜群ですね。

さて、プログラムは以下のようになります。

calc_pi_ramanujan.pyfrom fractions import Fraction

def frac_to_str(value: Fraction, index: int = 20) -> str:
    assert index > 0, "index must be positive."

    numerator: int = value.numerator
    denominator: int = value.denominator

    v1 = str(numerator // denominator)

    value = numerator % denominator
    v2 = ""
    while index > 4000:
        value *= 10 ** 4000
        v2 += str(value // denominator).zfill(4000)
        index -= 4000
        value %= denominator
    v2 += str(value * 10 ** index // denominator).zfill(index)
    return "{}.{}".format(v1, v2)

def calc_better_sqrt2(acc: int = 10) -> Fraction:
    a = Fraction(1)
    
    for _ in range(acc):
        a = (a + 2 / a) / 2
    
    return a

def ramanujan(sqrt2: Fraction, n_max: int = 10) -> Fraction:
    f1 = 1
    f2 = 1

    frac_list = []
    frac_list.append(Fraction(1103))
    for n in range(1, n_max + 1):
        for j in range(4 * (n - 1) + 1, 4 * n + 1):
            f1 *= j
        f2 *= n

        numerator = (1103 + 26390 * n) * f1
        denominator = (4 ** n * 99 ** n * f2) ** 4
        frac_list.append(Fraction(numerator, denominator))
    
    answer = sum(frac_list)
    answer *= Fraction(2 * sqrt2.numerator, 99 * 99 * sqrt2.denominator)
    return Fraction(answer.denominator, answer.numerator)

sqrt2 = calc_better_sqrt2()
pi = ramanujan(sqrt2)
print(frac_to_str(pi, 500))

ramanujan 関数で公式を計算しています。これを実行すると、以下のような結果が得られます。

3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803526230219797187632957009423169884173997169687127054201241817636932927549339638976777993988421323908253930847418652836475728322132688222434323492540827877237307302830564052644298876287266719096120119428671333763858725168076986843870668429848021845045129117254385272357912022365370603534402433973550710250551123267073069962089793885795396813157638368393718426290437458892369016644861148598331177256589073046202826048

これは、小数点以下86桁が一致しています。一瞬でこの桁の小数点を求められたのは驚きですよね。

次は、n_max を増やしてみましょう。n_max を20にして計算してみたところ、結果は以下のようになりました。

3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270672161890497068122605866023059509151705195556477427525213495775190128589195159828343925618497808887233400501510689066384972173652707535242978520630412657762302531685350510887427467367879555678036650218461468510187743495749089750878571125731064321972606932758413280273195217825364846509212304443500058840526327076172148266781094961385

それなりの時間で求められたのではないでしょうか。精度としては、小数点以下167桁が一致しました。

では次に、マチンの公式と同じくらいの精度を求めるには、どうすればよいのかということを実験してみましょう。
n_max を1500にして、calc_better_sqrt2 に渡す引数を20に変更しましょう。時間は必然的に掛かりますが、ものは試しです。一応 frac_to_str に渡す引数も増やして、20000にしておきましょう。つまり、

calc_pi_ramanujan.pysqrt2 = calc_better_sqrt2()
pi = ramanujan(sqrt2, n_max=20)
print(frac_to_str(pi, 500))

を、

calc_pi_ramanujan.pysqrt2 = calc_better_sqrt2(20)
pi = ramanujan(sqrt2, n_max=1500)
print(frac_to_str(pi, 20000))

に変更します。

ここでは、小数点以下11982桁が一致しました。ちょっと精度が足りないですね。

次に、n_max を1600にしてみました。
つまり、

calc_pi_ramanujan.pysqrt2 = calc_better_sqrt2(20)
pi = ramanujan(sqrt2, n_max=1750)
print(frac_to_str(pi, 20000))

に変更です。
そうすると、小数点以下12780桁が一致しました。これでマチンの公式の精度を超えることになります。

ではそうなるとここで気になるのは、どちらの方が速く計算できるか？ということですよね。
なので、ここでは各々10回ほど回して、その平均を取ることで求めてみましょう。

まず、マチンの公式の方を調べます。calc_pi_machin.py のコードを、

calc_pi_machin.pyfrom fractions import Fraction
import time

def frac_to_str(value: Fraction, index: int = 20) -> str:
    assert index > 0, "index must be positive."

    numerator: int = value.numerator
    denominator: int = value.denominator

    v1 = str(numerator // denominator)

    value = numerator % denominator
    v2 = ""
    while index > 4000:
        value *= 10 ** 4000
        v2 += str(value // denominator).zfill(4000)
        index -= 4000
        value %= denominator
    v2 += str(value * 10 ** index // denominator).zfill(index)
    return "{}.{}".format(v1, v2)

n1 = 9000
n2 = 3000

start = time.time()
for _ in range(10):
    array1 = [Fraction((-1) ** n, (2 * n + 1) * 5 ** (2 * n + 1)) for n in range(n1)]
    array2 = [Fraction((-1) ** n, (2 * n + 1) * 239 ** (2 * n + 1)) for n in range(n2)]
    sum1 = sum(array1)
    sum2 = sum(array2)
    answer = 16 * sum1 - 4 * sum2
end = time.time()

print((end - start) / 10)
# print("result: {}".format(frac_to_str(answer, index=20000)))

と変更します。
これで実行すると出力は、

41.52840092182159

となりました。あと数回実行してみると、

71.68818614482879

75.18734085559845

となっています。

次に、ラマヌジャンの公式の方も確かめてみましょう。
calc_pi_ramanujan.py のコードを、

calc_pi_ramanujan.pyfrom fractions import Fraction
import time

def frac_to_str(value: Fraction, index: int = 20) -> str:
    assert index > 0, "index must be positive."

    numerator: int = value.numerator
    denominator: int = value.denominator

    v1 = str(numerator // denominator)

    value = numerator % denominator
    v2 = ""
    while index > 4000:
        value *= 10 ** 4000
        v2 += str(value // denominator).zfill(4000)
        index -= 4000
        value %= denominator
    v2 += str(value * 10 ** index // denominator).zfill(index)
    return "{}.{}".format(v1, v2)

def calc_better_sqrt2(acc: int = 10) -> Fraction:
    a = Fraction(1)
    
    for _ in range(acc):
        a = (a + 2 / a) / 2
    
    return a

def ramanujan(sqrt2: Fraction, n_max: int = 10) -> Fraction:
    f1 = 1
    f2 = 1
    v1 = 1
    v2 = 1

    frac_list = []
    frac_list.append(Fraction(1103))
    for n in range(1, n_max + 1):
        f1 *= (4 * (n - 1) + 1) * (4 * (n - 1) + 2) * (4 * (n - 1) + 3) * (4 * n)
        f2 *= n

        numerator = (1103 + 26390 * n) * f1
        v1 *= 4
        v2 *= 99
        d1 = v1 * v2 * f2
        denominator = d1 * d1 * d1 * d1
        frac_list.append(Fraction(numerator, denominator))
    
    answer = sum(frac_list)
    answer *= Fraction(2 * sqrt2.numerator, 99 * 99 * sqrt2.denominator)
    return Fraction(answer.denominator, answer.numerator)

start = time.time()
for _ in range(10):
    sqrt2 = calc_better_sqrt2(20)
    pi = ramanujan(sqrt2, n_max=1600)
end = time.time()

print((end - start) / 10)
# print(frac_to_str(pi, 20000))

と変更します。
これで実行すると結果は、

20.70260441303253

となりました。あと数回実行すると、

20.455145359039307

20.36321837902069

となっています。

さて、これを比較すると、ラマヌジャンの公式の方が、マチンの公式より速く精度の高い円周率を求められることが分かります。
ちなみに今回は $\sqrt{2}$ の値をテキストファイル等に保存していないので、その分ラマヌジャンの公式の方は演算速度が遅くなっています。この値を保存し毎回読み込むなどして calc_better_sqrt2() の実行回数を減らすと、もっと早く円周率を求めることすらできます。
ラマヌジャンの公式の方が、複雑ではありますが、階乗の値を保存するなどすることによって、素早く収束の速い級数を計算することができるということです。

ラマヌジャンの公式を試してみる

実際にラマヌジャンの公式をシミュレーションできるHTMLを埋め込みました。
もしよろしければお試しください。
こちらでは、ラマヌジャンの公式を1~10回計算したときの結果の移り変わりを示しています。

ほとんど結果に差がありませんね。それほどこの公式は収束が速いのです。
これより細かい値については、Pythonで調べてみてください。

おわりに

本日は様々な（パソコンを使った）方法を使って円周率を求めてきましたが、いかがでしたでしょうか。
円周率は多くの人に知られた無理数でありますが、それだけに先人たちが考えてきたことも「桁違いに」多かったということでしょうか（しつこいですね、すみません）。

最後までお読みいただき、ありがとうございました。
よろしければ付録の方もご覧ください。
明日の夏ブログリレー2023の担当者はtoruthiさんです。

（付録1）ライプニッツの公式について

こちらでは、先述のライプニッツの公式

$$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

について、ご説明します。
ここではマクローリン展開というものを使って、説明しようと思います。
とはいえ、この記事を読んでいただいているのは高校生の方が特に多いと思いますので、高校三年生の「微積分」と、わずかな大学数学の知識を使って、この式が成り立つことを（ふんわりとですが）説明しますね。

まずマクローリン展開については、「高校数学の美しい物語」さんのこちらの記事を参考にさせていただきます。

先ほどのページによりますと、これはテイラーの定理を用いると証明できるとのことです。
ここではマクローリン展開を証明することは省略させていただくことにします。

また、理由については詳しく説明はしませんが、$\tan x$ の逆関数である $\arctan x$ も、このマクローリン展開によって表すことができます。
$\arctan x$ は、$y=\tan \theta (-\frac{\pi }{2}<\theta <\frac{\pi }{2})$ について、$\theta =\arctan y$ が成り立つような関数です。
例を挙げると、例えば $\arctan 1=\frac{\pi }{4}$ です。これは、$\tan \frac{\pi }{4}=1$ が成り立つことから求められます。

ただこの関数をマクローリン展開するには、$\arctan x$ の微分を求めなければならないことになります。
高校数学における「逆関数の微分」を使って、この微分を求めてみましょう。

$y=\arctan x$ として、$\frac{\mathrm{d}y}{\mathrm{d}x}$ を求めます。
このとき、$x=\tan y$ です。したがって、商の微分公式より

$$\frac{\mathrm{d}x}{\mathrm{d}y}={\left(\frac{\sin y}{\cos y}\right)}^{\prime }=\frac{(\sin y{)}^{\prime }\cos y-\sin y(\cos y{)}^{\prime }}{{\cos }^{2}y}=\frac{1}{{\cos }^{2}y}$$

ですね。もちろん $\frac{\mathrm{d}x}{\mathrm{d}y}=(\tan y{)}^{\prime }=\frac{1}{{\cos }^{2}y}$ と直接求めていただいても構いません。

さて、ここで、$y$ を残したままにするのはまずいので、$y=\arctan x$ として $x$ を戻してきましょう。これより、

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}={\cos }^{2}y={\cos }^2(\arctan x)$$

とできます。

ところで、三角関数の式である ${\sin }^2\theta +{\cos }^2\theta =1$ であることから求められる、$1+{\tan }^2\theta =\frac{1}{{\cos }^2\theta }$ を用いれば、

$$1+{\tan }^2(\arctan x)=\frac{1}{{\cos }^2(\arctan x)}$$

が求められます。また、先ほどの定義より、$\tan (\arctan x)=x$ となります。
これらを用いて ${\cos }^2(\arctan x)=$ の式に書き換えると、

$${\cos }^2(\arctan x)=\frac{1}{1+{\tan }^2(\arctan x)}=\frac{1}{1+x^2}$$

とできます。
以上から、

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{1+x^2}$$

となります。

次に、$\frac{1}{1+x^2}$ を微分していくわけですが、ライプニッツの公式から分かる通り、これは一般的なk階微分を求めなければならないのです。
これを全て手でやるのは至難の業です。
実際に僕も手を動かして5階微分くらいまで求めましたが、規則性のようなものはなく、どうしようかとネットを探してみたところです。
math-juken.comさんのこちらのページに参考になるものがありました。
今回僕らは $f^{(k)}(0)$ を求められれば良いので、どうもそこまで複雑なことをやる必要はないようです。

まず、先ほどのライプニッツの公式とはまた違うライプニッツの公式をお示しします。

参考ページによれば、これは帰納法で証明できるということです。
一応証明しておきましょう。

（証明）
(ⅰ) $n=1$ のとき、

$$\{f(x)g(x){\}}^{\prime }=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$$

したがって、成り立つ。

(ⅱ) $n=j$ のとき、

$$\{f(x)g(x){\}}^{(n)}=\sum _{k=0}^n{}_n{C}_k{f}^{(k)}(x)g^{(n-k)}(x)$$

すなわち、

$$\{f(x)g(x){\}}^{(j)}=\sum _{k=0}^j{}_j{C}_k{f}^{(k)}(x)g^{(j-k)}(x)$$

が成り立つと仮定する。

このとき、

$$\{f(x)g(x){\}}^{(j+1)}={\left\{\sum _{k=0}^j{}_j{C}_k{f}^{(k)}(x)g^{(j-k)}(x)\right\}}^{\prime }$$

が成り立つので、

$$\begin{array}{rl}\{f(x)g(x){\}}^{(j+1)}& ={}_j{C}_0{f}^{(1)}(x)g^{(j)}(x)+{}_j{C}_0{f}^{(0)}(x)g^{(j+1)}(x)+{}_j{C}_1{f}^{(2)}(x)g^{(j-1)}(x)+{}_j{C}_1{f}^{(1)}(x)g^{(j)}(x)+\cdots \\ & +{}_j{C}_{j-1}{f}^{(j)}(x)g^{(1)}(x)+{}_j{C}_{j-1}{f}^{(j-1)}(x)g^{(2)}(x)+{}_j{C}_j{f}^{(j+1)}(x)g^{(0)}(x)+{}_j{C}_j{f}^{(j)}(x)g^{(1)}(x)\\ & ={}_j{C}_0{f}^{(0)}{g}^{(j+1)}(x)+({}_j{C}_0+{}_j{C}_1)f^{(1)}(x)g^{(j)}(x)+\cdots +({}_j{C}_{j-1}+{}_j{C}_j)f^{(j)}(x)g^{(1)}(x)+{}_j{C}_j{f}^{(j+1)}(x)g^{(0)}(x)\end{array}$$

と変形できる。

ところで、二項係数の公式で、

$${}_n{C}_r={}_{n-1}{C}_{r-1}+{}_{n-1}{C}_r$$

という式、および

$$\begin{gathered} {}_j{C}_0=1={}_{j+1}{C}_0 \\ {}_j{C}_j=1={}_{j+1}{C}_{j+1} \end{gathered}$$

より、

$$\begin{array}{rl}\{f(x)g(x){\}}^{(j+1)}& ={}_{j+1}{C}_0{f}^{(0)}{g}^{(j+1)}(x)+{}_{j+1}{C}_1{f}^{(1)}(x)g^{(j)}(x)+\cdots +{}_{j+1}{C}_j{f}^{(j)}(x)g^{(1)}(x)+{}_{j+1}{C}_{j+1}{f}^{(j+1)}(x)g^{(0)}(x)\\ & =\sum _{k=0}^{j+1}{}_{j+1}{C}_k{f}^{(k)}(x)g^{(j+1-k)}(x)\end{array}$$

が成り立つ。

したがって、$n=j+1$ のときも

$$\{f(x)g(x){\}}^{(n)}=\sum _{k=0}^n{}_n{C}_k{f}^{(k)}(x)g^{(n-k)}(x)$$

が成り立つ。

ゆえに、帰納法より、もとの命題は成り立つ。　　■

さて、ここまでくると、先ほどのページの内容に則って、

$$f^{(2n)}(0)=0,f^{(2n-1)}(0)=(-1{)}^{n-1}(2n-2)!$$

と求められます。

これを、先ほどのマクローリン展開の式

$$f(x)=\sum _{k=0}^{\infty }{f}^{(k)}(0)\frac{x^k}{k!}$$

に代入しましょう。

先ほどの式 $f^{(2n-1)}(0)=(-1{)}^{n-1}(2n-2)!$ を使って、とくに $k$ が奇数で、$p$ を非負整数とするとき、以下のように求められます。

まず、$k=4p+1$ のとき、

$$f^{(4p+1)}(0)=f^{\{2(2p+1)-1\}}(0)=(-1{)}^{2p}(4p)!=(4p)!$$

となり、$k=4p+3$ のとき、

$$f^{(4p+3)}(0)=f^{\{2(2p+2)-1\}}(0)=(-1{)}^{2p+1}(4p+2)!=-(4p+2)!$$

となります。
これと、任意の偶数 $k$ について、$f^{(k)}=0$ であることを用いれば、先ほどの式は、そもそも $f(x)$ が $\arctan x$ であることを用いれば、

$$\begin{array}{rl}\arctan x& =0+\frac{0!}{1!}x+0+\frac{-2!}{3!}{x}^3+0+\frac{4!}{5!}{x}^5+0+\frac{-6!}{7!}{x}^7+\cdots \\ & =x-\frac{1}{3}{x}^3+\frac{1}{5}{x}^5-\frac{1}{7}{x}^7+\cdots \end{array}$$

と変形できます。これにより、$\arctan x$ をマクローリン展開することができました。

ここまで来ればあとはそのままです。先ほどの $\arctan x$ の例で、$\arctan 1=\frac{\pi }{4}$ であることを例示しました。ここでも $x=1$ を代入すると、

$$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

と求められます。
これで、もとのライプニッツの公式を求めることができました。

（付録2）ニュートン法について

こちらでは、ニュートン法について説明します。
ニュートン法を説明すると以下のようなものです。

ニュートン法については、「高校数学の美しい物語」さんのこちらの記事が参考になります。

実際のところでは、先ほどの方程式は、

$$0=f^{\prime }(a)(b-a)+f(a)$$

という方程式に変形できます。なぜなら、$f^{\prime }(a)\ne 0$ という条件下で

$$\begin{gathered} f^{\prime }(a)(b-a)=-f(a) \\ b-a=-\frac{f(a)}{f^{\prime }(a)} \\ b=a-\frac{f(a)}{f^{\prime }(a)} \end{gathered}$$

と変形でき、これはまた逆も成り立つからです。

で、$0=f^{\prime }(a)(b-a)+f(a)$ の意味するところとしては、ある直線 $y=f^{\prime }(a)(x-a)+f(a)$ は、点 $(b,0)$ を通るということです。さらに、点 $(a,f(a))$ も通ります。つまり $b$ というのは、$y=f(x)$ 上で $x$ 座標が $a$ である点における接線と、$x$ 軸の交点の $x$ 座標です。
関数 $f(x)$ が $f(x)=p{x}^2+q$ で表されるなら、以下の図がまさにそれです。

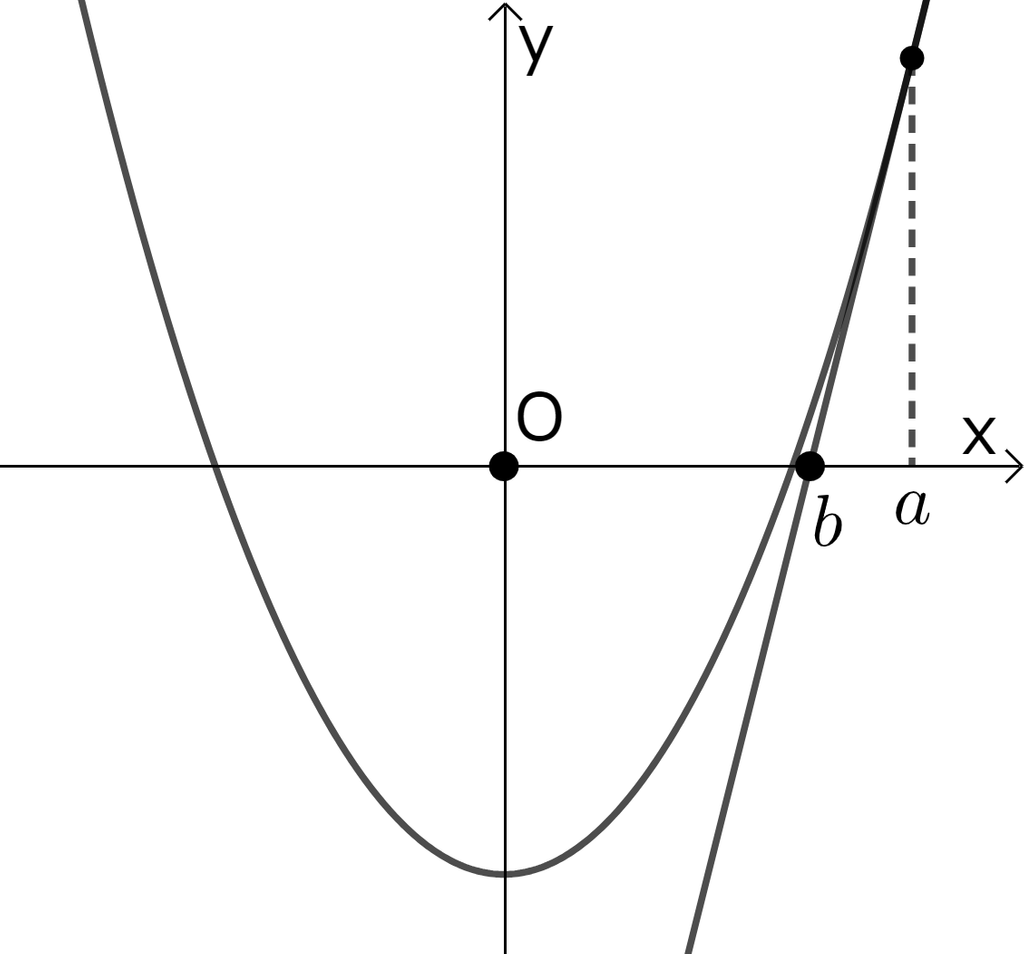
（GeoGebraで作成しています。）

そうしたら、また $b$ を $a$ にして、その点で接線を求め、それと $x$ 軸の交点の $x$ 座標を調べ……とすれば、いつかは $y=f(x)$ と $x$ 軸の交点の $x$ 座標と $b$ が一致しそうな気がしませんか？
直感的にはそういった理解になります。

実際、今回のニュートン法では、$f(x)=x^2-2$ と置いています。こうすると、$f(x)=0$ の解は $\pm \sqrt{2}$ ですから、$\sqrt{2}$ に限りなく近い値を $a$ として、ニュートン法のアルゴリズムを適用すれば求められるというお話にはなります。$f^{\prime }(x)=2x$ ですから、

$$b=a-\frac{a^2-2}{2a}=a-\frac{a}{2}+\frac{1}{a}=\frac{a}{2}+\frac{1}{a}=\frac{1}{2}\left(a+\frac{2}{a}\right)$$

が得られます。
この証明($a>\sqrt{2}$ の場合)については、先ほどの記事をご覧ください。

ただここでは、初期値として $1$ を選択しています。これは $\sqrt{2}$ より小さいため、先ほど与えられる証明では不十分です。そこで、$a>0$ ならば先ほどの方法で求められること、また同時に正の数 $t$ の平方根を求めるため、$f(x)=x^2-t$ とおいて、その式がこの方法を用いると、$\alpha$ の近似解を得られることをざっくりとですが示したいと思います。

$f(x)=x^2-t$ とおく。このとき、$f^{\prime }(x)=2x$ となる。こうすると、

$$b=a-\frac{f(a)}{f^{\prime }(a)}=a-\frac{a^2-t}{2a}=a-\frac{a}{2}+\frac{t}{2a}=\frac{1}{2}\left(a+\frac{t}{a}\right)$$

と求められる。以降、初項 $a_1=a$, 漸化式が

$$a_{n+1}=\frac{1}{2}\left(a_n+\frac{t}{a_n}\right)$$

で与えられる数列 $\{a_n\}$ を考える。

このとき、

$$a_{n+1}-a_n=\frac{1}{2}\left(a_n+\frac{t}{a_n}\right)-a_n=\frac{t}{2a_n}-\frac{a_n}{2}$$

を満たす。ここで

$$\frac{\mathrm{d}}{\mathrm{d}{a}_n}\left(\frac{t}{2a_n}-\frac{a_n}{2}\right)=-\frac{t}{2a_n^2}-\frac{1}{2}=-\frac{a_n^2+t}{2a_n^2}<0$$

となり、

$$\begin{gathered} \underset{x\to -0}{\lim }\left(\frac{t}{2x}-\frac{x}{2}\right)=-\infty \\ \underset{x\to +0}{\lim }\left(\frac{t}{2x}-\frac{x}{2}\right)=\infty \end{gathered}$$

となるから、$y=\frac{t}{2x}-\frac{x}{2}$ のグラフは、以下のようになる。

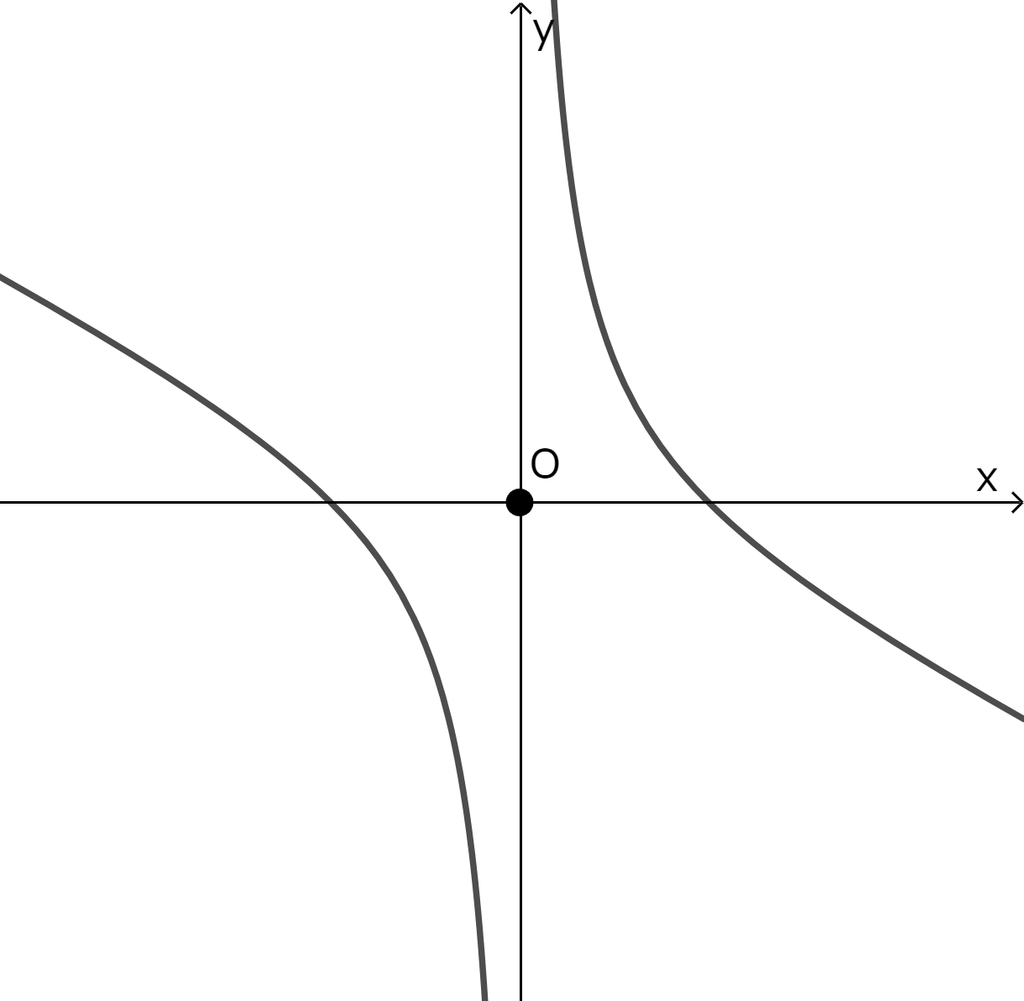
GeoGebraで作成。

さて、$y=\frac{t}{2x}-\frac{x}{2}$ と $x$ 軸の交点の $x$ 座標は、$0=\frac{t}{2x}-\frac{x}{2}$ を満たすから、$x=\pm \sqrt{t}$ である。
これとグラフの形状より、$a_n>0$ においては、$a_n<\sqrt{t}$ のとき、$a_{n+1}-a_n>0$, $a_n>\sqrt{t}$ のとき、$a_{n+1}-a_n<0$ となる。

次に、$a_n>\sqrt{t}$ のときを考える。

$$a_{n+1}-\sqrt{t}=\frac{t}{2a_n}+\frac{a_n}{2}-\sqrt{t}=\frac{t+a_n^2-2a_n\sqrt{t}}{2a_n}=\frac{(a_n-\sqrt{t}{)}^2}{2a_n}$$

であり、$a_n>0$ であるから、$a_{n+1}-\sqrt{t}$ の符号は0または$+$である。

ところで、$a_{n+1}-\sqrt{t}$ が0に等しいときは、$(a_n-\sqrt{t}{)}^2$ も0に等しいと言える。したがってこの時は、すでに $a_n$ が $\sqrt{t}$ と等しくなっている前提であり、今回は不適である。
これより、少なくとも $a_n$ が $\sqrt{t}$ に収束していないときは、$a_{n+1}-\sqrt{t}>0$、すなわち $\sqrt{t}<a_{n+1}$ である。

以上より、$a_n>\sqrt{t}$ のとき、$\sqrt{t}<a_{n+1}<a_n$ が成り立つから、$a_n>\sqrt{t}$ ならば、与えられた漸化式を繰り返し計算することにより、$a_n$ はいくらでも $\sqrt{t}$ に近づけることができる。

次に、$(0<)a_1<\sqrt{t}$ のときを考える。このとき、前の式と同様にすると、

$$a_2-\sqrt{t}=\frac{(a_1-\sqrt{t}{)}^2}{2a_1}$$

となる。$a_1<\sqrt{t}$ であるから、$a_2-\sqrt{t}>0$ である。ゆえに、$a_2>\sqrt{t}$ となる。

これは $a_n>\sqrt{t}$ のときに帰着するので、前述の通りやはり $a_n$ はいくらでも $\sqrt{t}$ に近づけることができる。

以上から、任意の正の数 $t$ について、$f(x)=x^2-t$ の場合、ニュートン法を適用して正の近似解を求めることができることを示しました。
これより、もちろん $t=2$ のときを考えることで、$\sqrt{2}$ を求めることができます。

付録もお読みいただきありがとうございました。
繰り返しになりますが、明日の夏ブログリレー2023の担当者はtoruthiさんです。