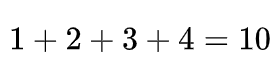四則演算で10を作る（テンパズル）

この記事は2023夏ブログリレー12日目の記事になります。

はじめに

初めまして。koukawa_ppです。
早いもので9月になってしまいました。今から100年前の1923年9月1日は、関東大震災があった日です。東工大の歴史のページによりますと、東工大が蔵前から現在の大岡山にキャンパスを移したのは、実はこの関東大震災があったからなのです。東工大の同窓会が蔵前工業会と言われているのも、たぶんこれが理由です。

もう一つ、9月1日と言われれば、皆さん月と日を足してちょうど10にしますよね？高校の先生が当てる生徒を決めるときに、なぜか計算するあれです。
そこで早速ですが、皆さんは「テンパズル」というパズルをご存知でしょうか？
「テンパズル」とは、かっこを用いた四則演算で、与えられた4つの数字から10を作るというパズルです。昔中学時代に、一緒によく帰った部活の先輩が車のナンバープレートでやっていたのを今でも鮮明に覚えています。

さて、そんなテンパズルですが、時に難問にぶち当たりますよね。順番が固定されていればともかく、そうでない場合は、並べかえる場合の数、挿入する演算子の場合の数、演算順序の場合の数で、それはもう人では総当たりできないくらい大きい数になります。そのため、基本的には一つの数字を固定して、残りの数字で考えるという方法が一般的な解法と言われていますが、手元にパソコンを用意していただければ、この総当たりも一瞬で終わらせることができます。そういうわけですから、今回はパソコンで、全ての場合の数を総当たりすることによって、求めてみようというお話です。

今回はPythonを使いますが、なんと今回はサードパーティ製のライブラリを一切使わず、Pythonの標準ライブラリだけで実装します。なので、Pythonのバージョンさえ足りていれば、特段準備しなくても実行できますので、ぜひ遊んでみてください。
もしPythonやプログラムが分からなくても大丈夫です。アルゴリズムの部分も若干説明しますし、ページの最後では実際にお試しできるようにしてありますので、最後だけ見てみるというのも大歓迎です。
今回使用するファイルは、すべて以下からダウンロードできます。

formula_str.py

数式を文字列にするためのPythonファイルです。

formula_str.py

9 KB

make_ten.py

四則演算で10を作るためのPythonファイルです。

make_ten.py

4 KB

cmd_make_ten.py

コマンドプロンプトからmake_ten.pyを実行するためのPythonファイルです。

cmd_make_ten.py

755 Bytes

なお、こちらのページで公開しているプログラムは、全てMITライセンスの下での扱いを許諾いたします。

開発環境

Windows 10 Home 64bit
Python 3.11.4
Visual Studio Code

どうやって総当たりするの？

まずは、どうやって総当たりするのかを考える必要があります。

計算する数字が4つ与えられているのはその通りなのですが、先ほども書いた通り、

演算子の並べ方
演算の順序（演算子の適用順）
（数字の並べ方）

という3つの要素があります。
最後の部分に関しては、実際並べかえないという縛りプレイもあるので、必ずしも考慮しなければならないということではありませんが、とりあえずこれら3つの要素を考えたプログラムを作成する必要があります。

演算子の並べ方はどうするの？

まずは、演算子の並べ方について考えましょう。

1 + 2 \times 3 - 4

上のように、4つの数字を演算して一つの答えを出す場合、間にそれぞれ一つずつ演算子を挿入すればよいので、つまり3つの演算子をランダムに決定すればよいことになります。

パソコンやプログラムで「モノ」を表現するに当たっては、それらを数字に置き換えることが最もやりやすいやり方です。そこで、 formula_str.py 内に、以下のような列挙体を定義しました。

formula_str.pyfrom enum import Enum

class Ope(Enum):
    PLUS = 0
    MINUS = 1
    MULTI = 2
    DIVIDE = 3

これを使って、とりあえず演算子は0~3の数字で表せるようにしました。このことを踏まえ、演算子の並べ方の候補を、以下のように列挙します。

make_ten.pycands = list(itertools.product(range(4), repeat=3))

今回知りました。itertools は最強だと。
これによって、0~3を使い、このうちの数字を3つ並べる全ての場合をlistに入れてくれました。

一応ですが、出力は以下のようになります。

[(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 0, 3), (0, 1, 0), (0, 1, 1), (0, 1, 2), (0, 1, 3), (0, 2, 0), (0, 2, 1), (0, 2, 2), (0, 2, 3), (0, 3, 0), (0, 3, 1), (0, 3, 2), (0, 3, 3), (1, 0, 0), (1, 0, 1), (1, 0, 2), (1, 0, 3), (1, 1, 0), (1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 2, 0), (1, 2, 1), (1, 2, 2), (1, 2, 3), (1, 3, 0), (1, 3, 1), (1, 3, 2), (1, 3, 3), (2, 0, 0), (2, 0, 1), (2, 0, 2), (2, 0, 3), (2, 1, 0), (2, 1, 1), (2, 1, 2), (2, 1, 3), (2, 2, 0), (2, 2, 1), (2, 2, 2), (2, 2, 3), (2, 3, 0), (2, 3, 1), (2, 3, 2), (2, 3, 3), (3, 0, 0), (3, 0, 1), (3, 0, 2), (3, 0, 3), (3, 1, 0), (3, 1, 1), (3, 1, 2), (3, 1, 3), (3, 2, 0), (3, 2, 1), (3, 2, 2), (3, 2, 3), (3, 3, 0), (3, 3, 1), (3, 3, 2), (3, 3, 3)]

天才ですね。

これより、この0をPLUS, 1をMINUS, 2をMULTI, 3をDIVIDEと関連付けさせ、それに則って計算を行えばいいわけです。
たとえば指定された数字を2, 5, 6, 4の順番として、この中から(3, 1, 2)とされたら、3はDIVIDE, 1はMINUS, 2はMULTIと対応付ければよいので、

2 \div 5 - 6 \times 4

とすればよいわけです。
ではここからは、演算順序を決定する方法を模索しましょう。

演算順序はどう決定するの？

演算子は、先ほども示した通り一つの式に3つあります。
なので、それら演算子には0番目、1番目、2番目とマークをすることによって、全ての演算順序を列挙することができます。
そのためには、数字の0から2をランダムに並べた全ての場合を取得すればよいことが分かります。

例を挙げましょう。

1 + 2 \times 3 - 4

といった数式があるとします。
この数式は、実のところ以下の数式と全く同じ意味を持ちます。

1 + (2 \times 3) - 4

それはもちろん、掛け算は足し算や引き算より優先されるためです。
次のように書いても変わりません。

(1 + (2 \times 3)) - 4

このようにかっこの書き方は何通りかあれど、上の3つの式は、
$\times$ , $+$ , $-$ の順番で計算することに変わりありません。
これを、(1, 0, 2) というように表したらどうでしょうか。

では、先ほどの式で $+$ , $\times$ , $-$ の順番で計算する場合は、

(1 + 2) \times 3 - 4

と表記すればよいです。これについても、

((1 + 2) \times 3) - 4

とか表記しても良いです。ただいずれにせよ、
$+$ , $\times$ , $-$ の順番で計算していることには変わりなく、
これを、(0, 1, 2) というように表せないでしょうか。

このように考えると、0から2を、重複せずにランダムに並べた全ての場合を取得する方法があればよいわけです。

make_ten.pyorders = list(itertools.permutations(range(3)))

今回知りました。itertools は最強だと。（2回目）
これによって、0~2をランダムに並べる場合の全てをlistにぶっこんでくれました。

一応ですが、出力は以下のようになります。

[(0, 1, 2), (0, 2, 1), (1, 0, 2), (1, 2, 0), (2, 0, 1), (2, 1, 0)]

天才ですね。
この程度なら手で全部追加してやろうかと思いましたが、ライブラリに頼った方が圧倒的に便利です。

さて、あとはこの cands と orders について2重でforループを回して検索すればいいわけですが、まあいかんせんPythonのforループは遅いと評判です。
ましてや2重ループなんて言ったら何と言われるか。
そんなわけで、少しでも調べる手間を省く方法が必要になります。

そこで目を付けたのが、全てが加減算か乗除算の場合です。
この場合、どこから計算したとしても、計算結果は等しくなることが知られています。
いや、正確には違いますね。

1 - (2 + 3) \neq = 1 - 2 + 3 1 \div (2 \times 3) \neq = 1 \div 2 \times 3

ではあります。しかし、考えてみましょう。

1 - (2 + 3) = 1 - 2 - 3 1 \div (2 \times 3) = 1 \div 2 \div 3

であるはずなので、結局全ての演算子の組み合わせを調べるのであれば、かっこが付いてようが付いてなかろうがいつかは調べるはずです。
しかもこうすることで、後で出てくる同じような正解を減らせるはずです。

これより、全てが加減算、または乗除算の場合は、order を (0, 1, 2) に固定して（すなわちいつでも最初から順番に演算するようにして）、その場合だけ調べるようにしてしまえば、その分の時間短縮を狙えるはずです。

それが以下の部分です。

make_ten.pyif (Ope.PLUS.value not in cand) and (Ope.MINUS.value not in cand):
    try:
        if _four_to_three(opes, cand, (0, 1, 2), Fraction(n1), Fraction(n2), Fraction(n3), Fraction(n4)) == Fraction(result):
            answers.append((Ope(cand[0]), Ope(cand[1]), Ope(cand[2]), 0, 1, 2))
    except ZeroDivisionError:
        pass
elif (Ope.MULTI.value not in cand) and (Ope.DIVIDE.value not in cand):
    if _four_to_three(opes, cand, (0, 1, 2), n1, n2, n3, n4) == result:
        answers.append((Ope(cand[0]), Ope(cand[1]), Ope(cand[2]), 0, 1, 2))

_four_to_three とは何かということについては、この後説明しますね。
ここでは、与えたcand, order, n1(Fraction(n1)), n2(Fraction(n2)), n3(Fraction(n3)), n4(Fraction(n4)) について、適切に演算子を用いて計算する関数だと思ってください。

はい、なぜ加減算の場合と乗除算の場合を分けているのか、ということですが、まあ誤差って怖いじゃないですか……。
割り算をした際に、割り切れない場合を扱うことだってしょっちゅうあるはずです。
そこで今回はFractionを使いました。
実際難しいテンパズルでは分数を使うみたいなので、小数で正確性を取るDecimalよりも、時間はかかるかもしれませんが厳密なFractionを使うことにします。

あと乗除算の場合については、ZeroDivisionErrorを捕捉しています。
理由は単純です。正解ではありえない場合において、運が良すぎるとゼロ除算をしてしまうためです。
たとえば以下のような場合が考えられます。

1 \div (1 - 1) + 1

まあ乗除算のみの場合においては0を指定されない限りはあり得ないんですが、一応ということで置いてあります。

上記のelif節の次のelse節は素直です。
ordersについてforループを回して、全ての演算順序について調べています。

make_ten.pyelse:
    for order in orders:
        if Ope.DIVIDE.value in cand:
            try:
                if _four_to_three(opes, cand, order, Fraction(n1), Fraction(n2), Fraction(n3), Fraction(n4)) == Fraction(result):
                    answers.append((Ope(cand[0]), Ope(cand[1]), Ope(cand[2]), order[0], order[1], order[2]))
            except ZeroDivisionError:
                pass
        else:
            if _four_to_three(opes, cand, order, n1, n2, n3, n4) == result:
                answers.append((Ope(cand[0]), Ope(cand[1]), Ope(cand[2]), order[0], order[1], order[2]))

こちらは、もちろんゼロ除算があればZeroDivisionErrorを捕捉し、そうでなければシンプルに調べています。

どうやって計算するの？

さて、前回の章から、総当たりをする方法は求められました。
そうするとここでは、

数字
演算子
演算順序

の3つを与えられたときに、どうすればうまく演算できるかということを考える必要があります。

考え方としては、以下の通りです。

_four_to_three関数で一番目の演算子を計算する
_three_to_two関数で二番目の演算子を計算する
_two_to_one関数で最後の演算子を計算する

たとえば、 $(1 + 2) \times (3 - 4)$ という式を与えられたら、

(1 + 2) \times (3 - 4) = 3 \times (3 - 4) = 3 \times (- 1) = - 3

という感じです。
そうすると、

_four_to_three関数で演算対象の数字を4つから3つにできる
_three_to_two関数で演算対象の数字を3つから2つにできる
_two_to_one関数で演算対象の数字を2つから1つにできる

ことに気づきます。
これが各々の関数の命名規則です。

先ほどの式 $(1 + 2) \times (3 - 4)$ については、 $+$ -> $-$ -> $\times$ という演算順なので、その順番に演算子を適応したという感じです。そこで、

_fout_to_three関数でこの式の $+$ を
_three_to_two関数でこの式の $-$ を
_two_to_one関数でこの式の $\times$ を

それぞれ演算しようという試みです。

さて、この考え方を基に、_four_to_three 関数を見ていきましょう。

make_ten.pydef _four_to_three(opes: list[Callable[[int | Fraction, int | Fraction], int | Fraction]], cand: tuple[int, int, int], order: tuple[int, int, int], n1: int | Fraction, n2: int | Fraction, n3: int | Fraction, n4: int | Fraction) -> int | Fraction:
    if order.index(0) == 0:
        return _three_to_two(opes, cand, order, opes[cand[0]](n1, n2), n3, n4)
    elif order.index(0) == 1:
        return _three_to_two(opes, cand, order, n1, opes[cand[1]](n2, n3), n4)
    elif order.index(0) == 2:
        return _three_to_two(opes, cand, order, n1, n2, opes[cand[2]](n3, n4))
    else:
        raise IndexError()

まず、先ほどの3つの関数が共通で受け取る引数に

opes
cand
order

がありますが、candとorderはそれぞれ先ほどのcandsとordersをforループしたときに得た要素です。一応ですが、cand はどの演算子を用いるか、order はどんな順番で演算子を用いるかを表したものです。

一方、opesは、_make_number内で初期化しています。

make_ten.pyopes: list[Callable[[Union[int, Fraction], Union[int, Fraction]], Union[int, Fraction]]] = []
opes.append(lambda x, y: x + y)
opes.append(lambda x, y: x - y)
opes.append(lambda x, y: x * y)
opes.append(lambda x, y: x / y)

opesをざっくり言えば、ラムダ式で演算を定義したものを追加したリストです。
つまり、opes[0](1, 2)とすれば、1+2=3が返ってきます。
このopesの順番はOpe列挙体の順番と対応しているので、Opeのvalueを取ってopesのインデックスに指定すれば該当する演算をするCallableを取得できます。
たとえば、以下のようにできます。

print(opes[Ope.MINUS.value](2, 1))  # 1  (2 - 1)

ということでもう一回_four_to_three関数を見てみましょう。

make_ten.pydef _four_to_three(opes: list[Callable[[int | Fraction, int | Fraction], int | Fraction]], cand: tuple[int, int, int], order: tuple[int, int, int], n1: int | Fraction, n2: int | Fraction, n3: int | Fraction, n4: int | Fraction) -> int | Fraction:
    if order.index(0) == 0:
        return _three_to_two(opes, cand, order, opes[cand[0]](n1, n2), n3, n4)
    elif order.index(0) == 1:
        return _three_to_two(opes, cand, order, n1, opes[cand[1]](n2, n3), n4)
    elif order.index(0) == 2:
        return _three_to_two(opes, cand, order, n1, n2, opes[cand[2]](n3, n4))
    else:
        raise IndexError()

order.index(0)を用いることで、最初(0番目)に演算するべき演算子のインデックスが分かります。
これが0か1か2によって処理が変わりますね。

ここから、ちょっとばかり一般的なお話をまじえて、この関数の説明をします。
ここで、 $a, b, c, d$ を数字として、 $@_{1}, @_{2}, @_{3}$ を演算子としましょう。
そのなかで、以下のような数式を考えましょう。

a @_{1} b @_{2} c @_{3} d

仮にorder.index(0)が0なら、最初の演算子 $@_{1}$ を最初に計算するので、_three_to_twoに渡す数字は、

n_{1} = a @_{1} b, n_{2} = c, n_{3} = d

となりますね。

同様にorder.index(0)が1なら、二つ目の演算子 $@_{2}$ を最初に計算するので、_three_to_twoに渡す数字は、

n_{1} = a, n_{2} = b @_{2} c, n_{3} = d

となります。

order.index(0)が2なら、最後の演算子 $@_{3}$ を最初に計算するので、_three_to_twoに渡す数字は、

n_{1} = a, n_{2} = b, n_{3} = c @_{3} d

となります。

もしorder.index(0)が3以上となると、これは四つ目の演算子や五つ目の演算子があることになるので、明らかに値が間違いです。
なので、IndexErrorを投げています。

次に、three_to_two関数を見ましょう。

make_ten.pydef _three_to_two(opes: list[Callable[[int | Fraction, int | Fraction], int | Fraction]], cand: tuple[int, int, int], order: tuple[int, int, int], n1: int | Fraction, n2: int | Fraction, n3: int | Fraction) -> int | Fraction:
    if order.index(1) == 0:
        return _two_to_one(opes, cand, order, opes[cand[0]](n1, n2), n3)
    elif order.index(1) == 1:
        if order.index(0) == 0:
            return _two_to_one(opes, cand, order, opes[cand[1]](n1, n2), n3)
        elif order.index(0) == 2:
            return _two_to_one(opes, cand, order, n1, opes[cand[1]](n2, n3))
        else:
            raise IndexError()
    elif order.index(1) == 2:
        return _two_to_one(opes, cand, order, n1, opes[cand[2]](n2, n3))
    else:
        raise IndexError()

この際、order.index(1)が0または2のときは_four_to_threeと変わらないです。
0のときは一つ目と二つ目の数字を演算すればいいですし、2のときは二つ目と三つ目の数字を演算すればよいです。

しかし、order.index(1)が1の場合は実は二パターンあります。

a @_{1} b @_{2} c @_{3} d

たとえば上の式において、orderが(0, 1, 2)の場合は、 $a @_{1} b$ が最初に計算されるので、

n_{1} = a @_{1} b n_{2} = c n_{3} = d

となります。ゆえに二つ目の演算子 $@_{2}$ を適用するのは、 $n_{1}$ と $n_{2}$ になります。
ただし、orderが(2, 1, 0)の場合は、 $c @_{3} d$ が最初に計算されるので、

n_{1} = a n_{2} = b n_{3} = c @_{3} d

となります。ゆえに二つ目の演算子 $@_{2}$ を適用するのは、 $n_{2}$ と $n_{3}$ となります。
このように、order.index(1)が1のときは、order.index(0)の値によって、 $n_{1}$ と $n_{2}$ に $@_{2}$ を適用するか、 $n_{2}$ と $n_{3}$ に $@_{2}$ を適用するかが変わります。
この条件を分けているのが、

make_ten.pyelif order.index(1) == 1:
    if order.index(0) == 0:
        return _two_to_one(opes, cand, order, opes[cand[1]](n1, n2), n3)
    elif order.index(0) == 2:
        return _two_to_one(opes, cand, order, n1, opes[cand[1]](n2, n3))
    else:
        raise IndexError()

この部分です。
それ以外のorder.index(1)の場合分けは、_four_to_threeと同様です。

次に、two_to_one関数を見ましょう。

make_ten.pydef _two_to_one(opes: list[Callable[[int | Fraction, int | Fraction], int | Fraction]], cand: tuple[int, int, int], order: tuple[int, int, int], n1: int | Fraction, n2: int | Fraction) -> int | Fraction:
    return opes[cand[order.index(2)]](n1, n2)

これは何も困ることはありません。
なぜなら、 $n 1$ と $n 2$ しか数字が与えられておらず、これについて最後の演算子を適用すればいいだけです。
ゆえに、

make_ten.pyreturn opes[cand[order.index(2)]](n1, n2)

となります。

以上の三つの関数

_four_to_three
_three_to_two
_two_to_one

を使うことによって、

演算子
演算順序
数字

の三つを与えられた式を、計算することができることが分かりました。
次に、答えをどのように表示するかを考えます。

どうやってかっこを付けるの？

さて、条件を満たす

演算子
演算順序
数字

が見つかったとします。
たとえば1, 1, 5, 8の三つの数字で10を作るとき、

8 \div (1 - 1 \div 5) = 10

とできます。

これは、8, 1, 1, 5と数字が与えられたとき、candは(3, 1, 3)と与えられ、orderは(2, 1, 0)と与えられたときの数式になります。
では、このようにorderとcandが与えられたとき、どのようにかっこを配置すればよいのか、そういった問題が出てきます。

この方法を見つけるべく、Googleを探すことにしました。
探すと、こんなYahoo知恵袋を見つけました。
ここによれば、数式を二分木で表現することによって、簡単にかっこの必要の有無を判別できる、というお話です。

二分木ってそもそも何？

まず二分木というものについてお話する前に、木構造というものについてお話する必要があります。

こちらが木構造のWikipediaのページになります。
木構造とは、というのを端的に伝えるのは難しいのですが、高校生や中学生の皆さんにとって一番なじみ深い具体例としては、樹形図が挙げられるでしょうか。若干不正確な言い方になりますが、ノードと呼ばれる要素同士を、エッジと呼ばれる線で結んだものを木構造と言います（では正確には、という話ですが、一つの例としては木構造内では閉路、すなわち一周できてしまうようなノードとエッジの繋ぎかたはしてはいけません）。
木構造で表すと良いものの例として、筑波大学さんのこちらのページが参考になります。
東京工業大学（今のところはですね。今後は東京科学大学になります。再編されるのかな？）を根ノードとして、その子ノードとして理学院とか工学院とかがあり、またその子ノードとして、例えば工学院なら機械系とか情報通信系とかがあります。
ここで理学院と工学院は兄弟ノードとなり、工学院は情報通信系から見れば親ノードです。

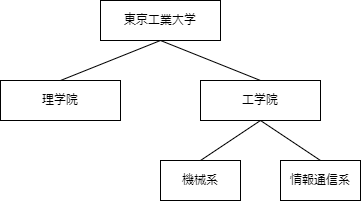
ちょうど上の図のようなものです。
本当は学院や系がもっとありますが、それらを含めて一つの「木」となります。
ここでいう「東京工業大学」、「工学院」、「情報通信系」といったものをノードと言います。
いわば頂点に君臨するノード、ここでは「東京工業大学」を根ノードと言います。
「工学院」にとって「情報通信系」、または「東京工業大学」にとって「理学院」のようなものを子ノードといい、逆の場合を親ノードと言います。
ここでは「理学院」、「機械系」、「情報通信系」のように、子ノードを持たないノードを葉と言います。

では二分木とは、ということですが、あるノードの持つ子ノードが高々2である木構造を言います。
つまり上の図の木構造は、実は二分木です。
実は、二分木の中でも、全てのノードが葉または子ノードを2つだけ持つ場合、これを全二分木というため、上の図の木構造は、二分木の中でもさらに全二分木です。
一応、こちらが二分木のWikipediaです。

どうやって二分木を実現するの？

次の問題としては、どうやって二分木をPythonで実現するかです。
まあこれはサードパーティ製のライブラリを使えばいいのですが、ここではサードパーティ製ライブラリ縛りをしているので、やむなく自力で実装します。

構造はこんな感じです。

名称	種別	説明
Node	class	二分木のノードを表します。
OpeNode	class	演算子を持つノードを表します。
NumNode	class	数字を持つノードを表します。ここでは葉になります。
FormulaBinaryTree	class	二分木のクラスです。
Ope	Enum	演算子を持つ列挙体です。
_make_formula_tree	メソッド	数式の二分木を作るメソッドです。
make_formula_str	メソッド	数字、演算子、演算順序を受け取って文字列にするメソッドです。外部からはこれをimportします。

各々はそこまで面倒ではないと思います。

Nodeクラスは、以下の通りです。

formula_str.pyclass Node(ABC):
    def __init__(self, number: int, content: str, content_index: int, parent: int) -> None:
        self.number = number
        self.content: str = content
        self.content_index: int = content_index
        self.parent: int = parent

numberは、ノードを識別するインデックスを表します。
contentは、演算子なら演算子を表す数字、数字なら数字を代入します。
content_indexは、演算子または数字を一意に識別するインデックスを表します。
たとえばこれが3番目の数字なら、content_indexには3が代入されています。
parentは、親ノードのnumberが入っています。

次に、OpeNodeクラスは、以下の通りです。

formula_str.pyclass OpeNode(Node):
    def __init__(self, number: int, content: str, ope_index: int, parent: int) -> None:
        super().__init__(number, content, ope_index, parent)
        self.is_left_operator: bool = True
        self.is_right_operator: bool = True
        self.left_child: int | None = None
        self.right_child: int | None = None
    
    @property
    def ope_index(self) -> int:
        return self.content_index
    
    def add_left_operator(self, child_num: int) -> None:
        self.left_child = child_num
    
    def add_right_operator(self, child_num: int) -> None:
        self.right_child = child_num
    
    def add_left_number(self, child_num: int) -> None:
        self.is_left_operator = False
        self.add_left_operator(child_num)
    
    def add_right_number(self, child_num: int) -> None:
        self.is_right_operator = False
        self.add_right_operator(child_num)

Nodeを継承しているので、Nodeの変数もまた保持しています。
他に、このノードの子ノードについての情報も持っています。
たとえば、is_left_operatorおよびis_right_operatorは、このノードの左の子ノードまたは右の子ノードがそれぞれOpeNodeであるか、すなわち演算子であるかを表します。
他にleft_childおよびright_childは、このノードの左の子ノードまたは右の子ノードのNodeのnumberを代入します。

次に、NumNodeクラスは、以下の通りです。

formula_str.pyclass NumNode(Node):
    def __init__(self, number: int, content: str, num_index: int, parent: int) -> None:
        super().__init__(number, content, num_index, parent)
    
    @property
    def number_index(self) -> int:
        return self.content_index

実体はNodeクラスと全く同じです。

次に、FormulaBinaryTreeクラスは、以下の通りです。
ただし、一部省略しています。

formula_str.pyclass FormulaBinaryTree:
    def __init__(self, content: str, ope_index: int) -> None:
        self.nodes: list[list[OpeNode], list[NumNode]] = [[], []]
        self._add_operator(content, ope_index, -1)
        self.none_list: list[tuple[int, int]] = [(0, 0), (0, 1)]
    
    def _add_operator(self, content: str, ope_index: int, parent: int) -> int:
        number = len(self.nodes[0])
        node = OpeNode(number, content, ope_index, parent)
        self.nodes[0].append(node)
        return number
    
    def _add_number(self, content: str, num_index: int, parent: int) -> int:
        number = len(self.nodes[1])
        node = NumNode(number, content, num_index, parent)
        self.nodes[1].append(node)
        return number
    
    def add_left_operator(self, content: str, ope_index: int, parent: int) -> None:
        num = self._add_operator(content, ope_index, parent)
        self[parent].add_left_operator(num)

        idx = self.none_list.index((parent, 0))
        self.none_list.remove((parent, 0))
        self.none_list.insert(idx, (num, 1))
        self.none_list.insert(idx, (num, 0))
    
    def add_right_operator(self, content: str, ope_index: int, parent: int) -> None:
        num = self._add_operator(content, ope_index, parent)
        self[parent].add_right_operator(num)

        idx = self.none_list.index((parent, 1))
        self.none_list.remove((parent, 1))
        self.none_list.insert(idx, (num, 1))
        self.none_list.insert(idx, (num, 0))
    
    def add_left_number(self, content: str, num_index: int, parent: int) -> None:
        num = self._add_number(content, num_index, parent)
        self[parent].add_left_number(num)
    
    def add_right_number(self, content: str, num_index: int, parent: int) -> None:
        num = self._add_number(content, num_index, parent)
        self[parent].add_right_number(num)
    
    def need_bracket(self, node_index: int) -> bool:
        if node_index == 0:
            return False
        
        if (self[node_index].content == '0' or self[node_index].content == '1') and (self[self[node_index].parent].content == '2' or self[self[node_index].parent].content == '3'):
            return True
        
        if self[node_index].number == self[self[node_index].parent].right_child and self[self[node_index].parent].is_right_operator:
            # self[node_index].parent -> node_index
            if (self[node_index].content == '0' or self[node_index].content == '1') and self[self[node_index].parent].content == '1':
                return True
            
            if (self[node_index].content == '2' or self[node_index].content == '3') and self[self[node_index].parent].content == '3':
                return True
        
        return False
    
    def _get_part_formula_str(self, node_idx) -> str:
        # 略
    
    def get_formula_str(self) -> str:
        return self._get_part_formula_str(0)
    
    def __str__(self) -> str:
        # 略

    def __getitem__(self, item) -> OpeNode:
        return self.nodes[0][item]

略したところはもちろん後で説明します。

まず、__init__におけるnodesについて説明します。
ここには、先ほど紹介したOpeNodeとNumNodeを追加します。
self.nodes[0]がOpeNode、すなわち演算子ノードのリスト、self.nodes[1]がNumNode、すなわち数字ノードのリストです。
また、最後の__getitem__によって、self.nodes[0]の要素を取得することができます。

まず、add_left_operatorおよびadd_right_operatorはそれぞれ、parentで指定されたOpeNodeについて、その左の子ノードまたは右の子ノードを、指定されたcontentおよびope_indexのOpeNodeにするメソッドです。

次に、add_left_numberとadd_right_numberはそれぞれ、parentで指定されたOpeNodeについて、その左の子ノードまたは右の子ノードを、指定されたcontentおよびnum_indexのNumNodeにするメソッドです。

どうやって二分木を作るの？

ではここからは、この二分木の作り方と使い方について、順を追って具体例を使って説明します。
ここでは先ほどの例

8 \div (1 - 1 \div 5) = 10

について説明します。すなわち、numbersは[8, 1, 1, 5]、opesは[3, 1, 3]、ordersは[2, 1, 0]と与えられたときについて説明します。

まず、FormulaBinaryTreeの初期化の部分は、根（ルート）のコンテンツおよびその演算子のインデックスを渡します。
二分木はあとに演算を行う演算子が根に近いように構成されるので、この二分木を作るときには、ordersの大きい値の方から作る必要があります。
それゆえ、_make_formula_tree関数においては、last_ope_indexが0になるので、まずopesの0番目の演算子について根を作る必要があります。
この時点での二分木は以下のようになります。

FormulaBinaryTreeを初期化すると、まず上図のように演算子ノードが追加されます。
次に、__init__内において、node_listなる変数を設定しています。
これは、この後の簡単のため、次にノードや葉が接続できそうなところを、タプル形式で納めたものになります。
たとえばここでは(0, 0)と(0, 1)が追加されていますが、この最初の0は、親ノードとなるノードの番号で、二つ目の0または1が、左か右かという数字になります。
一応、0なら左で、1なら右です。
なので、いうなればこの時点でこんな感じです。

次に、ope_indexは1になります。
このope_indexは、0番目のノードのope_indexである0より大きいので、この演算子ノードは根の右側に追加されます。
これより、この演算子ノードを追加した後の二分木は次のようになります。

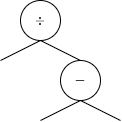
もちろんこの時、node_listも変更する必要があります。
node_listの要素のうち(0, 1)を、(1, 0)と(1, 1)に変更すればよいです。

最後に、ope_indexは2になります。

このope_indexは、0番目のノードのope_indexである0より大きいので、この演算子ノードは根の右側に追加されます。
さらに、その次のノードのope_indexは1であり、追加するノードのope_indexである2はこれより大きいから、ope_indexが1であるノードの、やはり右側に追加する必要があります。

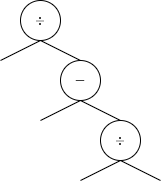
もちろんこの時、node_listも変更する必要があります。
node_listの要素のうち(1, 1)を、(2, 0)と(2, 1)に変更すればよいです。

こうすると、node_listの要素は、(0, 0), (1, 0), (2, 0), (2, 1)の4つになります。
これらに、数字ノードを順番に追加すればいいだけです。
順番とは8, 1, 1, 5ですから、この順に数字ノードを追加しましょう。

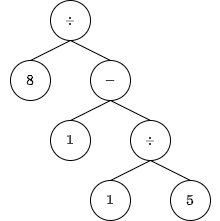
これで数式の二分木が完成します。
この二分木を作るコードは、以下の部分です。

formula_str.pydef _make_formula_tree(numbers: list[int], opes: list[int], orders: list[int]) -> FormulaBinaryTree:
    last_ope_index = orders.index(len(orders) - 1)
    formula_tree = FormulaBinaryTree(str(opes[last_ope_index]), last_ope_index)
    for index in range(len(orders) - 2, -1, -1):
        ope_index = orders.index(index)
        node_index = 0
        is_left = True
        while True:
            if ope_index < formula_tree[node_index].ope_index:
                if formula_tree[node_index].left_child == None:
                    break
                node_index = formula_tree[node_index].left_child
            elif ope_index > formula_tree[node_index].ope_index:
                if formula_tree[node_index].right_child == None:
                    is_left = False
                    break
                node_index = formula_tree[node_index].right_child
            else:
                raise IndexError()
        
        if is_left:
            formula_tree.add_left_operator(str(opes[ope_index]), ope_index, node_index)
        else:
            formula_tree.add_right_operator(str(opes[ope_index]), ope_index, node_index)
    
    for i in range(len(numbers)):
        if formula_tree.none_list[i][1] == 0:
            formula_tree.add_left_number(str(numbers[i]), i + 1, formula_tree.none_list[i][0])
        elif formula_tree.none_list[i][1] == 1:
            formula_tree.add_right_number(str(numbers[i]), i + 1, formula_tree.none_list[i][0])
    
    return formula_tree

最初のforループで演算子ノードを追加し、
二つ目のforループで数字ノードを追加します。

どうやってノードを文字で表すの？

さて、次の話ですが、
数列を表す文字列にする前に、ノードの繋がり方を一旦文字列にできるように、
__str__をオーバーライドすることにします。

formula_str.pydef __str__(self) -> str:
    searched = []
    answer = ""

    search_index = 0
    while True:
        n_idx = "nod{}({})".format(search_index, self[search_index].content)
        l_idx = "nod{}({})".format(self[search_index].left_child, self[self[search_index].left_child].content) if self[search_index].is_left_operator else "num{}({})".format(self[search_index].left_child + 1, self.nodes[1][self[search_index].left_child].content)
        r_idx = "nod{}({})".format(self[search_index].right_child, self[self[search_index].right_child].content) if self[search_index].is_right_operator else "num{}({})".format(self[search_index].right_child + 1, self.nodes[1][self[search_index].right_child].content)
        answer += "{} -> ({}, {})\n".format(n_idx, l_idx, r_idx)
        searched.append(search_index)

        if self[search_index].is_left_operator and self[search_index].left_child not in searched:
            search_index = self[search_index].left_child
        elif self[search_index].is_right_operator and self[search_index].right_child not in searched:
            search_index = self[search_index].right_child
        else:
            while not(self[search_index].is_right_operator) or self[search_index].right_child in searched:
                search_index = self[search_index].parent
                if search_index == -1:
                    break
                
            if self[search_index].is_right_operator and self[search_index].right_child not in searched:
                search_index = self[search_index].right_child
            else:
                break
        
    return answer

これの根本的な考え方は自然です。
根からノードを辿っていくとして、

ノード(コンテンツ) -> (左の子ノード(コンテンツ), 右の子ノード(コンテンツ))

を全ての演算子ノードについて出力すればよい、という考え方です。
このコードにおいては、演算子ノードを全て見つけて、それらすべてについて子ノードを全て出力するというものです。

これを使って、先ほどの条件、すなわち、numbersは[8, 1, 1, 5]、opesは[3, 1, 3]、
ordersは[2, 1, 0]と与えられたときの文字列を出力すると、以下のようになります。

nod0(3) -> (num1(8), nod1(1))
nod1(1) -> (num2(1), nod2(3))
nod2(3) -> (num3(1), num4(5))

なんとなくノードの形が分かったのではないでしょうか。
以下のように置き換えれば分かりやすいかもしれません。

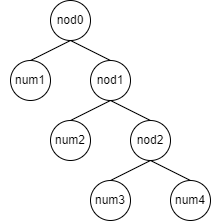
この図を文字列として表示すると、先ほどのような出力になります。

どうやって数式にするの？

さて、この二分木からどうやってかっこをつけて文字列にするかということですが、
これについては再帰的に関数を呼び出せばいいわけです。

たとえば先ほどの図については、nod0において、num1とnod1を表す数式を、適切な演算子で結合すればいいわけです。
ではそのnod1においては、num2とnod2を表す数式を、適切な演算子で結合すればいいわけです。
最後にそのnod2においては、num3とnum4を、適切な演算子で結合すればいいわけです。

さて、この一つのノードについて、
数式を表す文字列を求める関数を、get_part_formula_strとしています。

def _get_part_formula_str(self, node_idx) -> str:
    answer = ""
    if self.need_bracket(node_idx):
        answer += "("
        
    if self[node_idx].is_left_operator:
        answer += self._get_part_formula_str(self[node_idx].left_child)
    else:
        answer += self.nodes[1][self[node_idx].left_child].content
        
    if self[node_idx].content == '0':
        answer += " + "
    elif self[node_idx].content == '1':
        answer += " - "
    elif self[node_idx].content == '2':
        answer += " * "
    elif self[node_idx].content == '3':
        answer += " / "
    else:
        raise ValueError(self[node_idx].content)
        
    if self[node_idx].is_right_operator:
        answer += self._get_part_formula_str(self[node_idx].right_child)
    else:
        answer += self.nodes[1][self[node_idx].right_child].content
        
    if self.need_bracket(node_idx):
        answer += ")"
        
    return answer

この関数のアルゴリズムは至ってシンプルです。

かっこが必要なら(を加える。
左の子ノードが演算子ノードなら、そのノードについて_get_part_formula_strを再帰的に呼び出す。そうでなければ、その数字を出力する。
このノードに対応する演算子を出力する。
右の子ノードが演算子ノードなら、そのノードについて_get_part_formula_strを再帰的に呼び出す。そうでなければ、その数字を出力する。
かっこが必要なら)を加える。

これをすれば、適切にかっこを付けることができます。

どうやってかっこの要不要を判断するの？

では、かっこが必要か否かについては、どうやって判別しましょう。
これについては、need_bracket関数で知ることができます。
need_bracket関数は以下のようになっています。

formula_str.pydef need_bracket(self, node_index: int) -> bool:
    if node_index == 0:
        return False
        
    if (self[node_index].content == '0' or self[node_index].content == '1') and (self[self[node_index].parent].content == '2' or self[self[node_index].parent].content == '3'):
        return True
       
    if self[node_index].number == self[self[node_index].parent].right_child and self[self[node_index].parent].is_right_operator:
        # self[node_index].parent -> node_index
        if (self[node_index].content == '0' or self[node_index].content == '1') and self[self[node_index].parent].content == '1':
            return True
            
        if (self[node_index].content == '2' or self[node_index].content == '3') and self[self[node_index].parent].content == '3':
            return True
        
    return False

ここで重要なことは、加減算と乗除算の優先度の違いと、減除算の後ろにある演算です。
まず縦軸を親ノードの演算子、横軸を対象ノードの演算子として、かっこの要不要を表にしましょう。

	$+$	$-$	$\times$	$\div$
$+$
$-$	△	△
$\times$	○	○
$\div$	○	○	△	△

まず○の部分は、どういった状況でもかっこが必要な場合です。
つまり、親ノードが $\times$ または $\div$ で、対象ノードが $+$ または $-$ の場合は、必ずかっこを付けなければならないということになります。
これがコードの以下の部分です。

if (self[node_index].content == '0' or self[node_index].content == '1') and (self[self[node_index].parent].content == '2' or self[self[node_index].parent].content == '3'):
    return True

対象ノードのcontentが0または1なので、これは $+$ か $-$ を意味します。
そして、parentノードのcontentが2または3なので、これは $\times$ か $\div$ を意味します。
このとき、かっこは必要なのでTrueを返しています。

では、次に△とはどういうことか？ということですが、これは、親ノードより後ろにある場合のみかっこが必要という意味です。
例を挙げて説明しましょう。

(1 + 1) - 1 (= 1) 1 - (1 + 1) (= - 1)

(1 - 1) - 1 (= - 1) 1 - (1 - 1) (= 1)

上記の二セットの式は、どちらも $1 + 1$ または $1 - 1$ を、 $-$ より先に行うように示されている式です。
しかし、 $1 + 1$ または $1 - 1$ が $-$ の前にあるか否かで、結果が変わっていることも分かると思います。
ただし、この $-$ を $+$ に変えると、結果は変わらなくなります。

除算の場合も同様です。

(2 \times 2) \div 2 (= 2) 2 \div (2 \times 2) (= \frac{1}{2})

(2 \div 2) \div 2 (= \frac{1}{2}) 2 \div (2 \div 2) (= 2)

上記の二セットの式も、どちらも $2 \times 2$ または $2 \div 2$ を、 $\div$ より先に行うように示されている式です。
しかし、 $2 \times 2$ または $2 \div 2$ が $\div$ の前にあるか否かで、結果が変わっていることも分かると思います。
ただし、この $\div$ を $\times$ に変えると、結果は変わらなくなります。

このように、減除算の場合は、その演算子の後ろに加減算または乗除算がある場合に、かっこが必要になってくるのです。
このことをプログラムで表します。

まず、親ノードの演算子の後ろ側に対象ノードの演算子がある場合とは、ここでは親ノードの右の子ノードが対象ノードであることを意味します。
つまり、

formula_str.pyif self[node_index].number == self[self[node_index].parent].right_child and self[self[node_index].parent].is_right_operator:

を満たす場合ということになります。
self[self[node_index].parent].is_right_operatorを入れないと、右ノードが数字ノードであり、偶然インデックスが合致した場合も条件を満たしたと認識されてしまいます。

その後の条件はスムーズです。

formula_str.pyif self[node_index].number == self[self[node_index].parent].right_child and self[self[node_index].parent].is_right_operator:
    # self[node_index].parent -> node_index
    if (self[node_index].content == '0' or self[node_index].content == '1') and self[self[node_index].parent].content == '1':
        return True
            
    if (self[node_index].content == '2' or self[node_index].content == '3') and self[self[node_index].parent].content == '3':
        return True

このif節内の一つ目のif節は、node_indexノードのcontentが0または1、すなわち $+$ か $-$ のときで、かつparentノードのcontentが1、すなわち $-$ の場合、Trueを返します。

二つ目のif節も同様で、node_indexノードのcontentが2または3、すなわち $\times$ か $\div$ のときで、かつparentノードのcontentが3、すなわち $\div$ の場合、Trueを返します。

なお、これらいずれの条件にも合致しなかった場合、Falseを返します。

さて、ここまでのものを使ったのが、make_formula_str関数です。
好きな数字、演算子、演算順を指定して、この関数を呼び出して、その返り値をprintで出力してみてください。
多分求めている文字列を取得できます。

どうやって使うの？

さて、Pythonでこの三つのファイルを使えばうまく出来ます。
しかし、まずmake_ten.py内のmake_number関数を紹介しましょう。

make_ten.pydef make_number(n1: int, n2: int, n3: int, n4: int, result: int = 10, do_sort: bool = False) -> str:
    answer = []
    if do_sort:
        cands = list(set(itertools.permutations([n1, n2, n3, n4])))
        for cand in cands:
            answer.extend(_make_number(*cand, result=result))
    else:
        answer = _make_number(n1, n2, n3, n4, result=result)
    
    if len(answer) == 0:
        return "There is no answer."
    else:
        return "\n".join(answer)

これは、do_sortがFalseならば、_make_numberをそのまま呼び出して終了します。

ただし、do_sortがTrueの場合は、与えられた4つの数字の順番を入れ替えた場合を全て調べます。

make_ten.pycands = list(set(itertools.permutations([n1, n2, n3, n4])))

permutationsで全ての場合を一旦出力し、これをsetに入れることで重複要素を削除します。
その後再びlistに入れます。
というよりforループに入れるならsetのままでも良かったですね。
この関数を使うことで、どんな場合でも求めることができるはずです。

しかし、これだとどこかでmake_number関数を呼び出して、実行しなければなりません。
そうすると、数字が変わるたびにプログラムを変更して、実行し直す必要が出てきますが、このためにわざわざプログラムを開いて修正するのは手間なもの。
そこで、ここではコマンドプロンプトから呼び出せるように、少しプログラムを追加しましょう。

cmd_make_ten.py# Reference: https://qiita.com/stkdev/items/e262dada7b68ea91aa0c

import argparse

from make_ten import make_number

def get_args():
    parser = argparse.ArgumentParser()

    parser.add_argument("n1", metavar='N1', type=int)
    parser.add_argument("n2", metavar='N2', type=int)
    parser.add_argument("n3", metavar='N3', type=int)
    parser.add_argument("n4", metavar='N4', type=int)
    parser.add_argument("--result", type=int, default=10)
    parser.add_argument("--dosort", action='store_true')

    args = parser.parse_args()

    return (args)

def main():
    args = get_args()

    print(make_number(args.n1, args.n2, args.n3, args.n4, result=args.result, do_sort=args.dosort))

if __name__ == '__main__':
    main()

argparseは多くの場合に、コマンドライン引数を受け取りやすくするために使われています。

ここでは、必須の引数としてn1, n2, n3, n4を求め、任意の引数として、--resultと--dosortを用意しました。
n1からn4は、与える4つの数字です。
--resultは、作る数字です。デフォルトで10に設定されています。
--dosortは、これを指定すると、並び替えがありになります。

これは、以下のように実行できます。

python cmd_make_ten.py 1 1 5 8 --dosort

実際に実行してみると、きちんと結果が出力されると思います。
テンパズルはたくさんネットで出ているので、やってみるといいですね。

ここで実際に試す

今回のPythonのプログラムとほぼ同じ処理をするHTMLを下に埋め込みました。
もしよろしければお試しください。

n1, n2, n3, n4に、計算対象の4つの数字を入れ、resultに、計算結果としたい数字を入れてください。
do sortにチェックを入れると、並べかえた結果も出力されるようになります。

n1:

n2:

n3:

n4:

result:

do sort

また、このHTMLプログラムは、HTML+TypeScriptで作成しています。
作成したTypeScriptファイルと、これをVisual Studio 2022でビルドしたJavaScriptファイルは、下の通りです。
よろしければご覧ください。
なお、Visual Studio 2022は、ver. 17.7.0を使用しています。

app.ts

MakeTenのプログラムのTypeScriptバージョンです。これをビルドして下のJavaScriptを作成しています。

app.ts

22 KB

app.js

上のHTMLに埋め込まれているJavaScriptのコード。

app.js

19 KB