この記事は新歓ブログリレー2021 46日目の記事です。

はじめに

最近競プロを少し頑張ってるあみだです。
2月頃から書いてましたが適当にだらだらした結果もう4月です。

BIT(Binary Indexed Tree)という、競技プログラミングなどで用いられるデータ構造について話しています。
セグメント木(Segment Tree)の発展版っぽいやつです。

競プロ初心者なので用語の使い方がおかしいかもしれませんが、ご愛嬌。

導入

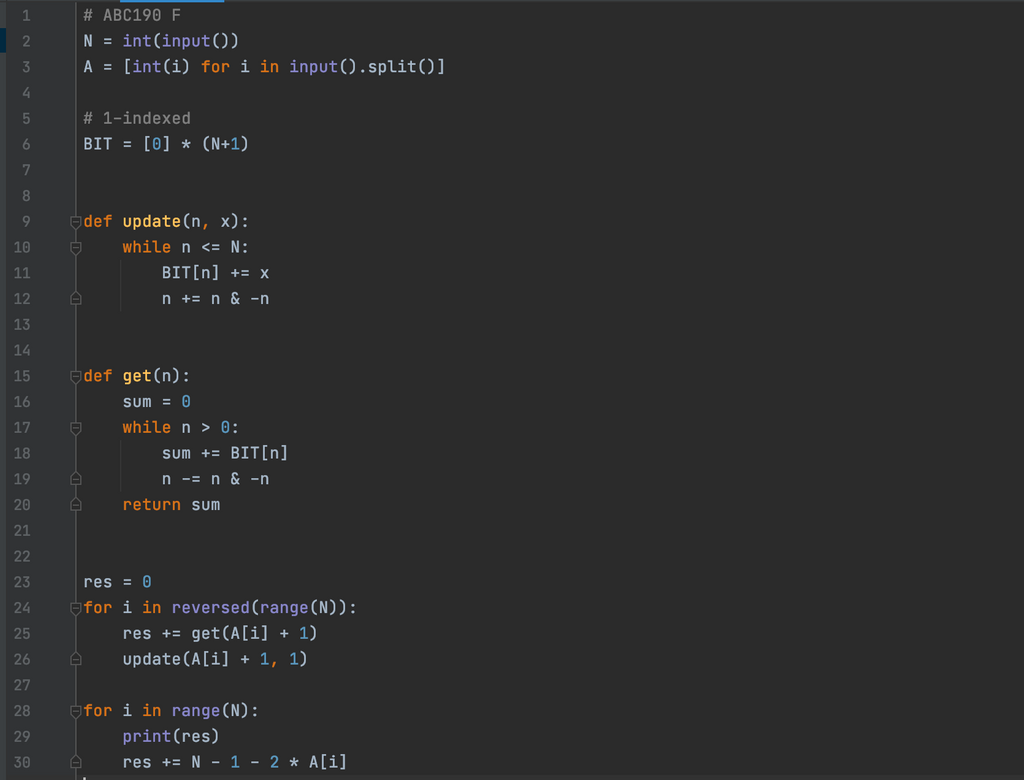
ABC190のF問題でBITに出会った。
色々調べたけどお気持ちだけの絵とか魔法の x&-x とかで意味がわからなかったので、もう少し厳密に理解したいと思ったのがこれを書いたきっかけ。

元ネタ論文(Fenwick, 1994, p.328)の発想が一番自然で理解しやすかったのでこれに習った。(とはいえ元ネタを見る前に自分で考えたものなので自己流解釈あるかも)

数式を使った証明メインでやっていきます。
間違いがあったら教えていただけると幸いです。
投稿者Twitter

そもそもBITとは

Binary Indexed Tree の略。
このデータ構造を木っぽく表したとき、高さが同じところのIndexをBinaryで見ると、いい感じになってることが由来だと思う。(これはBinary Indexed Tree のはなしの40Pあたりを見てほしい)

扱うBIT

恐らく一般的なBIT。
ある数列 ${a_{n}}$ があったとする。
要求は以下

一点更新をO(log $N$ )でできる
指定された範囲の合計 $k = i \sum j a_{k}$ をO(log $N$ )で求められる

1-indexedで考える。

具体的なデータ構造

大きさN+1の配列(名前をBITとする)
1-indexedなので事実上の大きさはN。

内訳

B I T [n] = k = n - f (n) + 1 \sum n a_{k}

f (n) \equiv (n を 割 り 切 る 最 大 の 2^{k})

(プログラム的には $f(n)=n&-n$ で、なんでそうなるのかはn&-nの謎にて)

要は、indexがn以下のf(n)個の要素の合計。
(ちょっと記述怪しいけど流石に読み取ってください)

これだとわかりにくいので例を挙げると、
BIT[8] = $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} + a_{6} + a_{7} + a_{8}$
BIT[9] = $a_{9}$
BIT[10] = $a_{9} + a_{10}$
BIT[11] = $a_{11}$
BIT[12] = $a_{9} + a_{10} + a_{11} + a_{12}$

一点更新について

$a_{n}$ に $x$ を加算する事を考える。

加算対象

B I T [g^{k} (n)] (k \in N)

ただし、

g (x) \equiv n + f (n)

g^{k} (n) \equiv k 回 g (g (. . . . g (n) . . .)

Pythonで書くとこんな感じ

update.pydef update(n, x):
    while n <= N:
        BIT[n] += x
        n += n&-n

上記の条件がa_nを更新することの必要条件であることを示すのは簡単だが、十分条件であることを示すのは厳しい。

必要条件であること

証明

帰納的に示す。

H (n) = {k \in N ∣ n - f (n) + 1 \leq k \leq n}

というようにnがカバーする範囲のようなものを定めると、以下が満たされていればいい。

H (n) \subseteq H (g^{k} (n))

まず、

n = m f (n) (m \in O)

と $2^{k}$ 部分を切り離して表せるので、

g (n) = n + f (n) = (m + 1) f (n) = \frac{m + 1}{2} 2 f (n)

$\frac{m + 1}{2}$ は整数だから、(mは奇数なので)以下のような不等式が成り立つ。

f (g (n)) \geq 2 f (n)

よって、

(n - f (n) + 1) - (g (n) - f (g (n)) + 1) = n - f (n) - (n + f (n) - f (g (n)) = f (g (n)) - 2 f (n) \geq 0 \Rightarrow g (n) - f (g (n)) + 1 \leq n - f (n) + 1

また、 $g (n)$ の定義より、 $n < n + f (n) = g (n)$

以上から、

H (n) \subseteq H (g (n))

つまり、 $g (n)$ は $n$ の範囲をカバーする。

$\subseteq$ は推移律を持つので、帰納的に

H (n) \subseteq H (g^{k} (n))

必要条件の証明終わり

十分条件であること

証明を書いている途中に力尽きました。
お気持ちとしては、 $f (m) = 2^{l}$ の $l$ を一個ずつ上げていって $n$ をカバーするものを探すと、結局 $m = g^{k} (n)$ しかないよね、という話です。

書きかけの証明は一応残しておきます。

証明

まず、

f (n) = f (n^{'}), n \neq = n^{'} \Rightarrow H (n) \cap H (n^{'}) = \emptyset

であることを示す。
要は、 $n$ をカバーする $H (m)$ が存在する時、他に $f (m) = f (l)$ で $H (l)$ が $n$ をカバーするような $l$ が存在し無いということを言いたい。
$f (m) = 2^{l}$ のラインに $n$ をカバーするものが存在するかしないか、するなら $m = g^{k} (n)$ なのかだけ示せばよくなる。

n < n^{'} - f (n^{'})

を示せば良い。

$n < n^{'}$ としてよく、

n = m f (n), n^{'} = m^{'} f (n^{'}) (m < m^{'}, m, m^{'} \in O)

$m, m^{'} \in O$ なので、 $m^{'} - m \geq 2$ だから、

n^{'} - f (n^{'}) - n = f (n) (m^{'} - m - 1) \geq f (m) > 0

よって、

f (n) = f (n^{'}), n \neq = n^{'} \Rightarrow H (n) \cap H (n^{'}) = \emptyset

すると、今後示すべきは以下になる。 $k = l o g_{2} f (n)$ とする。

各 $l \in N$ に対し、 $n \in H (o_{l} 2^{l + k}) (o_{l} \in O)$
となる $O_{l}$ が存在するならば、 $o_{l} 2^{l + k} = g^{p} (n)$ となる $p \in N$ が存在する。

ちょっと扱いづらいので、変形する。

n \in H (o_{l} 2^{l + k}) \Leftrightarrow (o_{l} - 1) 2^{k + l} + 1 \leq n \leq o_{l} 2^{l + k} \Leftrightarrow n \leq o_{l} 2^{l + k} \leq n + 2^{l + k} - 1

だから、以上のことは次のように言い換えられる。
各 $l \in N$ に対し、 $m \in [n, n + 2^{k + l} - 1], f (m) = 2^{k + l}$ となる $m \in N$ が存在するならば、 $g^{p} (n) = m なる p \in N が存在する。$

ここで証明は力尽きました。一応お気持ち説明をしておくと、
$m$ より大きい $2 f (m)$ の倍数の中でHがnを含む可能性がある(含むとは限らない)のは証明の最初で言った唯一性から最小のものであることがわかる。
そして、それは $g (m)$ なんだよ、ということが言える。

そうすると連鎖的に $H (g^{k} (n))$ がnを含むことはわかるけれども、 $f (g^{k} (n))$ を並べてみると飛び飛びに並んでしまう。

あとは、その間に抜けがないか、つまり $H (n) \in H (n^{'})$ だが、 $H (g (n)) \in H (n^{'})$ ではない $n^{'}$ が存在しないか、ということをチェックすればOK。

大小条件とかをちゃんと書くと、

n^{'} > g (n), f (n^{'}) > f (g (n)), H (n) \in H (n^{'}) \Rightarrow H (g (n)) \in H (n^{'})

を証明すればOKということ。

以上です、m(__)m

計算量

更新箇所は平均で $\frac{l o g _{2} N}{2} + 1$ 個
元ネタ論文(Fenwick, 1994, P332)には $\frac{l o g _{2} N}{2}$ って書いてある気がするけど(誤読してたらすみません)、計算&実験してみたらこうなってしまった...
まあ1しか違わないからヨシ！

Nが2の累乗のときの証明をする。(元ネタ論文もそのときに限ってた)
まあどうせO(log $N$ )なのでそれ以外でも誤差。

証明

BIT[n]は $f (n)$ 個の要素をカバーしてるので、
平均更新量Uは以下のように表せる。

U = \frac{\sum _{n = 1}^{N} f ( n )}{N}

そして、
$f (n) = 2^{m} (m \in N)$ となるようなN以下のnの個数を $Q_{m}$ とすると、
$m < l o g_{2} N$ のとき $Q_{m} = \frac{N}{2 ^{m + 1}}$ であり、 $m = l o g_{2} N$ のとき $Q_{m} = 1$ である。

この事の証明(思ったよりも長くなってしまった)

まず、
$m <$ $l o g$ $_{2} N$ のとき

Q_{m} = \frac{N}{2 ^{m}} - l = m + 1 \sum l o g_{2} N Q_{l}

$m =$ $l o g$ $_{2} N$ のとき $Q_{m} = 1$ と表せる。

$m <$ $l o g$ $_{2} N$ のときなんでこうなるかというのは、書き出して考えて見るとわかるかもしれない。
前半部は $2^{m}$ の倍数の個数、後半部は指数がmより大きいものの個数。

あとは帰納的に示せるが、ほとんど明らかなので細かいところは省略。

\frac{N}{2 ^{m}} - l = m + 1 \sum l o g_{2} N Q_{l} = \frac{N}{2 ^{m}} - l = m + 1 \sum l o g_{2} N - 1 \frac{N}{2 ^{l + 1}} + 1 = \frac{N}{2 ^{m}} - \frac{\frac{N}{2 ^{m + 2}} { 1 - ( \frac{1}{2} ) ^{l o g_{2} N - (m + 1)} }}{1 - \frac{1}{2}} + 1 = \frac{N}{2 ^{m}} - \frac{N}{2 ^{m + 1}} (1 - \frac{2 ^{m + 1}}{N}) + 1 = \frac{N}{2 ^{m}} - \frac{N}{2 ^{m + 1}} - 1 + 1 = \frac{N}{2 ^{m + 1}}

これがわかれば容易。

Q_mの証明終わり

なんで $Q_{m}$ なんてものを導入したかというと、Uの計算をするため。
$n = 1 \sum N$ は1ごとに上がって行き、当然1つずつ計算していく。
しかし、加算する値は $f (n)$ で決まっているので、 $f (n)$ で分類して足したほうがいいだろうというわけ。

それを踏まえると、

U = \frac{\sum _{i = 1}^{N} f ( n )}{N} = \frac{\sum _{m = 0}^{l o g_{2} N} 2 ^{m} Q _{m}}{N} = \frac{N + \sum _{m = 0}^{l o g_{2} N - 1} \frac{N}{2}}{N} = 1 + m = 0 \sum l o g_{2} N - 1 \frac{1}{2} = \frac{l o g _{2} N}{2} + 1

計算量の証明終わり

指定範囲の合計算出について

基本的には1からnまでの和なのだが、それを組み合わせることで任意の範囲に対応できる。
よって、1〜nまでの合計の算出を考えれば十分。

これは一点更新より簡単。

返す値

返す値を $S_{n}$ とする。

S_{n} = i = 1 \sum n a_{i} = B I T [n] + B I T [h (n)] + B I T [h^{2} (n)] + . . . + B I T [2^{k}] (k \in N)

$h (n) \equiv n - f (n)$
である。

Pythonで書くとこんな感じ

get.pydef get(n):
    sum = 0
    while n > 0:
        sum += BIT[n]
        n -= n&-n
    return sum

hを複数回適用することでいつかは $2^{k}$ になる(0は自然数ですよ？)
$f (2^{k}) = 2^{k} なので、 B I T [2^{k}] = i = 1 \sum 2^{k} a_{n}$ だからそれで終了

これが正しいことを示すのは簡単。
再帰的にできる。

証明

$S_{n} = i = 1 \sum n a_{i} = i = h (n) + 1 \sum n a_{i} + i = 1 \sum h (n) a_{i} = B I T [n] + S_{h (n)}$

あとは $h^{l} (n) が$ いつか $2^{k}$ に到達する(つまりは単調減少であること)を示せば良い。(といっても超簡単)
$h (n) - h (h (n)) = h (n) - (h (n) - f (h (n))) = f (h (n)) > 0$
$h (n) > h (h (n))$

以上。

計算量

元ネタ論文(Fenwick, 1994, P331)によると、参照する個数は”平均で” $\frac{l o g _{2} N}{2} + 1$ って書いてあった(誤読してなければ)
オーダー感覚としてはそうなんだが、証明は不明悲しい気持ちを表明。

ちなみに、実験してみて帰納的に導き出せた平均は

l o g_{2} N - 1 + \frac{l o g _{2} N + 2}{N}

だった。

まあ、
$h^{k} (n) \leq n - 2^{k + l o g_{2} f (n)} + f (n)$ だからオーダーはO(log $N$ )程度だろうというある程度の予想はつくし、OK

n&-nの謎

n&-n = (nを割り切る最大の2 $^{k}$ )

??????

そもそも-nとは

&はビット演算子なので-nの2進法表現について考える。

マイナスを定義する時の気持ちとしてはマイナス値でも加算を滞りなくやりたい。
まず、nはint型で、これは全部でk桁の2進数で表現されているとする。

ここで、コンピュータ上でのnはnを表しているとは限らないことに注意したい。
というのも、(基本的に)使える桁数には限りがあるからである。

足し算や引き算をする時、k桁を超える、あるいはk桁では引かれる方の数の桁数が足りないということは十分に考えられる。

その時、超えた分を切り捨てたり足りない桁を仮につけたりする。
これはつまり、

(コ ン ピ ュ ー タ 上 の n) = n + m 2^{k + 1} (m \in Z)

これを踏まえると、

x + (- x) = 2^{k + 1} \equiv 0 (m o d 2^{k + 1})

となるように

- x = 2^{k + 1} - x

と決めたほうが都合が良い。

ちなみにこれを「2の補数」というらしい。

ビット的には...

ビット反転(~)して+1する。
※~を数式に埋め込むのが出来なかったので、 $\sim$ (ニアリーイコール)を代わりに用いています...

ビット反転すると、1だったところは0になり、0だったところは1になる。
よって、

n + (\sim n) = k 桁 11 . . . 11 = 2^{k + 1} - 1

なので、

n + (\sim n + 1) = 2^{k + 1} \Rightarrow - n = 2^{k + 1} - n = (\sim n + 1)

となっている。

実用上は

k桁をフルに使って数字を表現すると、 $2^{k + 1} - 1 = - 1$ となって都合が悪いので、
k-1桁で数字本体を表現して、k桁目が0ならプラス、1ならマイナスというように解釈する。

例:) k=8とする。
1: 00000001, 15: 00001111, 100: 01100100
-1:11111111, -15:11110001, -100:10011100

n&-nの動き

n = k - a - 1 桁 . . . 1 a 桁 0

であったとする。
このとき、 $f (n) = 2^{a}$ である。

\sim n = k - a - 1 桁 . . . 0 a 桁 1

なので、
(※当然だが、k-a-1桁のところはnの同一箇所をビット反転したもの)

- n = \sim n + 1 = k - a - 1 桁 . . . 1 a 桁 0

(※k-a-1桁のところはnの同一箇所をビット反転したもの)

以上から、

n & - n = k - a - 1 桁 0 1 a 桁 0 = 2^{a} = f (n)

おわりに

応用範囲も広くなく、セグ木で十分実現できるらしいのであまり理解する必要はなかったのかもしれない。

そんなことよりもMarkdownのTeX環境でチルダをうまく表現する方法を誰か教えて下さい。

参考文献

Binary Indexed Tree のはなし
Peter M. Fenwick, "A New Data Structure for Cumulative Frequency Tables" (1994)

明日は @lum1narie さんです。
お楽しみに

BITについてちょっとだけ数学っぽく考えてみた【新歓ブログリレー46日目】

はじめに

導入

そもそもBITとは

扱うBIT

具体的なデータ構造

内訳

一点更新について

加算対象

必要条件であること

十分条件であること

計算量

指定範囲の合計算出について

返す値

証明

計算量

n&-nの謎

そもそも-nとは

ビット的には...

実用上は

n&-nの動き

おわりに

参考文献

関連する記事

BITについてちょっとだけ数学っぽく考えてみた【新歓ブログリレー46日目】

はじめに

導入

そもそもBITとは

扱うBIT

具体的なデータ構造

内訳

一点更新について

加算対象

必要条件であること

十分条件であること

計算量

指定範囲の合計算出について

返す値

証明

計算量

n&-nの謎

そもそも-nとは

ビット的には...

実用上は

n&-nの動き

おわりに

参考文献

この記事をシェア

関連する記事