定理証明で遊ぼう(しなさい)

こんにちは、stretchyboxです。
この記事はtraP夏のブログリレー 9月19日の記事です。

いよいよ夏休みも残り一週間ですね、皆さんは有意義で楽しい休みを送れましたか？
僕はずっと家で寝てました。

定理証明とは

定理証明(自動定理証明)とは、数学的な命題やプログラムの仕様を形式化してその証明を与え、そのコード(証明)が正しく書かれているかを定理証明器で確認することで正当性を検証する手法です。
具体的な用途としては四色問題やKepler予想といった複雑で誰も査読したがらないような数学の問題の証明であったり、高い安全性を求められるソフトウェアの検証に使われています。
今回はその中でも有名なCoqという定理証明器と、それを使って問題が解けるTopProverというサイトで遊んでみようと思います。

Coqの導入

Coq自体の導入は簡単でここのインストーラーを落としてポチポチしてればできます。デフォルトのCoqIDEが使いにくければProofGeneralやVScoqなどのエディタの拡張を使うこともできます。
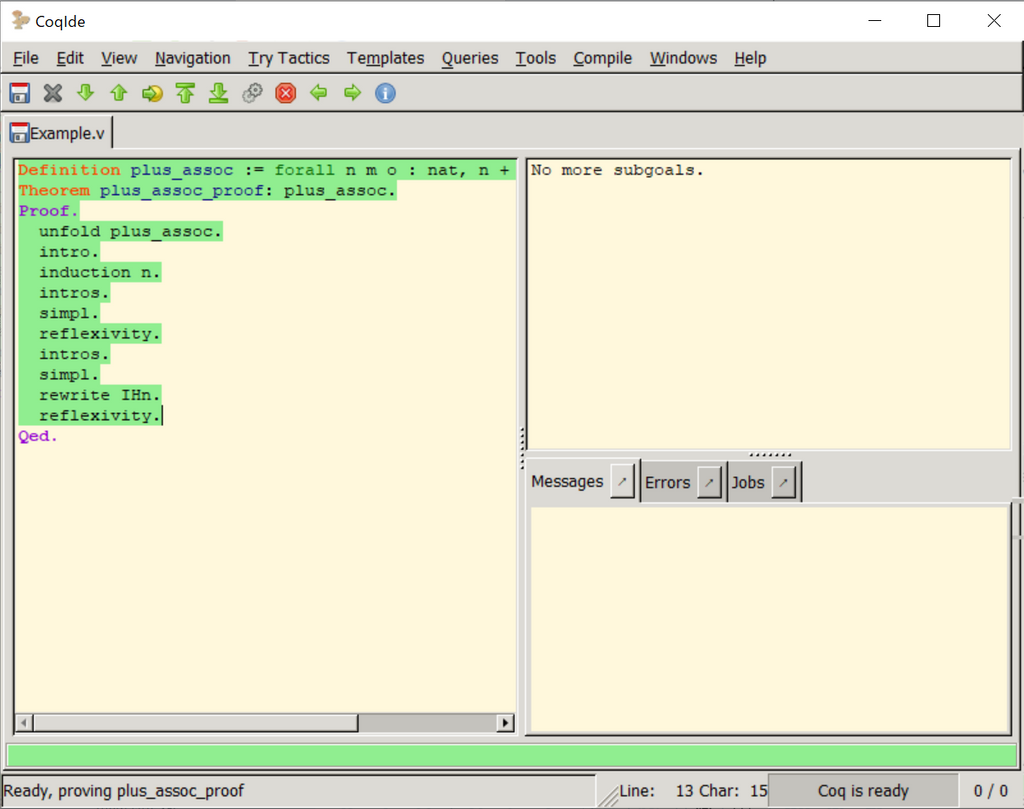
CoqIDEを起動すると左側にコードを書く部分、右上に示すべき式右下にエラーなどを表示する部分が現れます。ツールバーの右から三番目にある緑色の下向き矢印を押すと、"."区切りの文が読み込まれて、正しければコードが緑色になり、誤りがあればエラーが表示されます。証明のすべてが正しく読み込まれれば証明がなされたことになります。

問題 plus_assoc

問題文
示すべき式は

\forall n, m, o \in N n + m + o = n + (m + o)

です。加法は左結合なので自然数の加法における結合法則を表しています。
下の証明ではnに関する帰納法で示しています。

assoc.vDefinition plus_assoc := forall n m o : nat, n + m + o = n + (m + o).
Theorem plus_assoc_proof: plus_assoc.
Proof.
  unfold plus_assoc.
  intro.
  induction n.
  intros.
  simpl.
  reflexivity.
  intros.
  simpl.
  rewrite IHn.
  reflexivity.
Qed.

第一行で問題で与えられる示すべき命題の名前を定義していて、第二行でその命題の証明をこれからすることを示しています。ProofからQedまでの間にあるものは全てタクティックと呼ばれるもので仮定やいま示すべきもの(サブゴール)を変形したり、証明を終了させたりする命令です。

unfold plus_assocは示すものを定義で与えられた形に戻します。
introはサブゴールが→の形とき前半を仮定に移したり、forallの変数を一つ固定したりします。introsはintroを可能な限り実行します。
induction nはサブゴールをnに関する帰納法で示す形に変形します。
simplは関数適用を一回行ってサブゴールの形を変形します。ここでは0+m+oの左側の足し算を実行してm+oのような変形をしています。
rewrite IHnはサブゴール中のIHnの等式の左辺と一致してる部分を右辺に書き換えます。
reflexivityはサブゴールの証明を完成させるタクティックで左辺と右辺が等しい等式の時行うことができます。

実際にこのコードをコピペして一行ずつ動かしてみると、これらのタクティックがどのように働いているのかがなんとなく見えると思います。
詳しい説明はここをみるとこれらのタクティックの使い方がわかりやすく載っています。また、TopProverでは参加者のコードが見ることができるので上級者のコードを参照することも勉強になると思います。

参考文献

萩原　学『Coq/SSReflect/MathCompによる定理証明:フリーソフトではじめる数学の形式化』
基本的なCoqとSSReflectなどのライブラリの使い方が載っていてよいです。
Amazonリンク

おわりに

私の時間と実力が足りずCoqのほんの一部しか紹介できませんでしたが、興味がある方は萩原先生の本や公式ドキュメントに詳しく載っているので調べてみてください。TopProverでは毎週コンテストを行っていてratingもつくようになっているらしいです。私はまだ参加できていないのでこれから参加して強くなっていきたいですね。
明日はRLookさんの記事です。楽しみですね