こんにちは。実は今日4/13が誕生日の、情報工学系4年、オレスタです。祝ってね。

普段はサウンド班として活動している私ですが、最近は競技プログラミングにもハマっています。というわけで、プログラミング系の記事も書いてみようかな、と。
そっちに興味ある新入生多そうだし。

競技プログラミングとは、簡単に言うとプログラミングの問題を解くコンテストです。その中でも、AtCoderという会社が実施しているABC(AtCoder Beginner Contest)は、比較的初心者向けのコンテストであり、traPでも多くのメンバーが参加しています。
ABCでは毎回4問出題され、難易度が低い方からA～Dと問題番号が付けられています。D問題が解けるようになったらABCは卒業、ワンランク上のARC(AtCoder Regular Contest)に参加する…という流れになっているようです。

初めはC問題もおぼつかなかった私ですが、このごろはD問題まで何とか解けるようになりました。この成長のよろこびを共有したいな、ということで、初めてABCを全完出来た、第106回の問題を解説してみようかなと思います。

注意

当たり前ですが、ABC106のネタバレを含みまくっています。競技プログラミングに興味があり、自力で解いてみたい！　という人は、先に自分で解いてから読んでくださいね。

AtCoder Beginner Contest 106

A問題

問題文

縦Aヤード、横Bヤードの畑に、下図のような形で縦横に1ヤードの道を作る。この時、畑の面積は？

(　・ω・)小4の面積の問題で良く出てくる等積移動だな…　$S=(A-1)(B-1)$で行けるはず！

B問題

問題文
200以下の自然数Nに対し、以下の条件を満たす数の個数を求めなさい。

• N以下の自然数
• 奇数である
• 約数が8個ちょうど存在する

(　・ω・)約数の個数って言えば…素因数分解を使うんだよね、確か以下の3パターンのどれかだ。

$a^7:1/a/a^2/a^3/a^4/a^5/a^6/a^7$
$a^{3}b:1/a/a^2/a^3/b/ab/a^{2}b/a^{3}b$
$abc:1/a/b/c/ab/bc/ac/abc$

(　・ω・)$a^7$の最小値は$3^7=2187$…　うん、あり得ない。
(　・ω・)$a^{3}b$だったら…$3^3\times 5=135$、$3^3\times 7=189$　…だけだな
(　・ω・)$abc$はどうだ…？　$3\times 5\times 7=105$、$3\times 5\times 11=165$、$3\times 5\times 13=195$の3つっぽい。
(　・ω・)じゃあ、105、135、165、189、195の5つかな？　あとは条件分岐を連打すれば…

A = int(input())

if(A<105):
    print(0);
elif(A<135):
    print(1);
elif(A<165):
    print(2);
elif(A<189):
    print(3);
elif(A<195):
    print(4);
else:
    print(5);

(　^ω^)スマートさゼロの解答が出来たよ！

※後で気づいたこと↓
オンライン数列大辞典というサイトに「約数が8個の整数からなる数列」という非常に便利なモノがありましたので、ここから「200以下の奇数」を抜き出して来ればそれで済みました。

C問題

問題文
1～9が並んでいる数字列に対し、各数字について以下のような操作を行う。
【1→1】
【2→22】
【3→333】
【4→4444】
…以下9まで続く…

例えば、「123」という数字にこの操作を行うと「122333」となり、もう1回この操作を行うと「12222333333333」となる。

さて、ある数字列Sに対しこの操作を5000兆回行ったとき、左からK文字目は何になるか答えなさい。
(条件：Sは1文字以上100文字以内の数字列、Kは$10^{18}$以下の自然数)　←コレ超重要

(　・ω・)「2を$n$回操作すると、2が$2^n$個並ぶわけね、じゃあ$2^{5000000000000000}$っていくつなんだろう？」

print(2**5000000000000000);

#その後、消息が途絶える

(　；ω；)ｳｯ^[1]
(　˘ω˘)待てよ…

${\log }_{10}2=0.3010$
$5000{\log }_{10}2=1505$

(　・ω・)$2^{5000}$の時点で$10^{18}$なんて余裕で超えるじゃん、つまり…

(　・ω・)どうやって実装しようか…

(　＾ω＾)完全に理解した
、あとはコード書けばええやん

S = str(input());
K = int(input());

for i in S:
    if(i=="1"):
        if(K==1):
            print("1");
            break;
        else:
            K-=1;
    else:
        print(i);
        break;

D問題

(　・ω・)これまでD問題は解けたことがないんだけど、とりあえずやるだけやってみるか～

https://beta.atcoder.jp/contests/abc106/tasks/abc106_d
$N$個の駅を結ぶ電車があり、その駅には「1、2、3…　…N」というナンバリングがされている。
この路線には$M$本の電車が走っており、それらの電車が走る区間が駅番号で示されている。

このとき、「駅番号pから駅番号qの区間内だけを走る電車はいくつあるか？」という問いが$Q$個与えられるので、
これらの問いにすべて答えなさい。
(条件：$N\le 500,M\le 200000,Q\le 100000$)

(　・ω・)制限時間($3\text{sec}=\text{300～3000万くらい}$)を考えると、$MQ(=\text{200億くらい})$では到底間に合わなさそうだな…
(　・ω・)あれ？　$N\le 500$だけヤケに低くない？　$N^2$だったら間に合うのか？

(　・ω・)出発駅i、終着駅jである電車の数を表す配列として「trainList」っていうのを作ろう。
(　・ω・)そうしたら、trainListと別に「ansList」って答えを入れる配列を作って、そいつでfor文回せば行けるんじゃね？

(ここでしばらく考える)

(　・x・)よく考えたら、このままだとfor文回すにしても順番が上手く行かない気がしてきた…

※例を挙げて説明すると、「区間1～6」と「区間2～7」を先に求めれば「区間1～7」の計算に使える！　などと考えたのですが、このままでは、区間2～7の計算は区間1～7の計算よりも後に行われることになるため、利用できない…と考えました。

(　^ω^)そうだ、「始点と終点」じゃなくて「始点と区間の長さ」で配列作れば行ける！

(　・ω・)これで、答えの配列ansListを次のように実装すれば…行けるのでは？

($i<N$のとき　→　区間の長さが0のとき)
$\text{ansList}[i]=\text{trainList}[i]$

($i<2N$のとき　→　区間の長さが1のとき)
$\text{ansList}[i]=\text{trainList}[i]+\text{ansList}[i-N]+\text{ansList}[i-N+1]$
　※区間が1短い場合の計算結果は、既にansListで求めたのでそれを使用する！
　$[i-N]$→始点が同じで区間が1短い
　$[i-N+1]$→始点が1つ先で区間が1短い（つまりは、終点が同じで区間が1短い）

(それ以外のとき　→　区間の長さが2以上のとき)
$\text{ansList}[i]=\text{trainList}[i]+\text{ansList}[i-N]+\text{ansList}[i-N+1]-\text{ansList}[i-2\ast N+1]$
　※始点側が1短い区間と終点側が1短い区間とを比較すると、重複した部分が出てくる。
　例）区間[3,7]で考えると、区間[3,6]と区間[4,7]における答え、そして[3,7]を走る電車の数を足せばよい…のだが、
　　　区間[4,6]は[3,6]と[4,7]の両方でカウントしているため引く必要がある。
　　　イメージは集合の演算で、$A\cup B=A+B-A\cap B$という感じ。
　$i-2\ast N+1$→始点が1つ先で区間が2短い（つまりは、始点が1つ先で終点が1つ手前）

(；・ω・)これで…どうだ！！　←緊張

≫≫≫勝利≪≪≪

ｷﾀ━━━━━━━(ﾟ∀ﾟ)━━━━━━━!!

※このあたりで喜びのあまり絶叫、親に説教を受ける。

はい、という感じのABC106でした。読んでいただきありがとうございます。
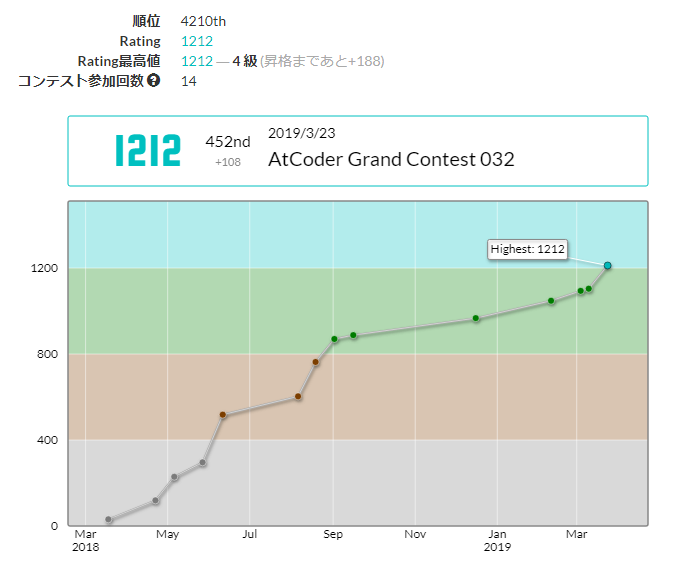
ちなみに、今ではAtCoderのレーティングは1212(水色)になりました。1200を超えるとABCは卒業になる^[2]ので、いよいよ次のステップに進んだんだなあ、という気持ち。
これからもがんばります。よろしくおねがいします。

余談

今夜、AtCoder Beginner Contest 124が開催されるようです！
競技プログラミングに興味があるのであれば、ぜひチャレンジしてみてください！
AtCoder Beginner Contest 124