この記事は新歓ブログリレー2019 3月27日(19日目)の記事です.
新入生の皆さん, 合格おめでとうございます!!
はじめまして, 18のwasabiです.
はじめに
この記事は, Haskellで定義されているいくつかの基本的なMonoidやSemigroupの紹介と最後にそれらを活用してみるというテーマの記事です.
この記事の内容は以下の通りです.
- Monoidについての説明
- いろいろなMonoidについてみていく
- 実際にMonoidをつかったコードを見てみる
この記事はHaskellがわかる人, 興味がある人向けです.
Monoidってなんだっけ?
Semigroup(半群)
まずMonoidの前にSemigroupについて説明します.
ある集合Sの任意の元a,b,cに対して, 結合法則
(a <> b) <> c = a <> (b <> c)
が成り立つとき, Sと<>を合わせてSemigroupといいます. たとえば, 整数の集合と足し算の組はSemigroupであることがわかります.
(1 + 2) + 3 = 1 + (2 + 3) = 6
HaskellではSemigroupという型クラスがこれを表しています.
class Semigroup a where
(<>) :: a -> a -> a -- 二項演算
また, 整数と掛け算の組もSemigroupです. このことからわかるように, 一つの集合に対して複数のSemigroupを定義できることに注意してください.
Monoid(モノイド)
MonoidはSemigroupの中でも, 下の性質を満たすある特別な元eがSに含まれているものです.
e <> x = x
x <> e = x
ただしxはSの任意の元です. このような元eを単位元といいます.
整数と足し算においては, 0が単位元のはたらきをすることがわかります.
1 + 0 = 1
0 + 3 = 3
HaskellではMonoid型クラスがこれを表しています.単位元eはHaskellではmemptyという名前がついています.
class Semigroup a => Monoid a where
mempty :: a -- 単位元
Semigroupと同様, Monoidも一つの集合に対して複数定義できます. 整数と掛け算のMonoidにおいて単位元が何かは自分で考えてみて下さい.
Monoidいろいろ
Haskellのライブラリで定義されているMonoidを見ていきましょう. 実装は実際のものとは異なるものもあります.
All, Any
これは, ブール値の論理和・論理積についてのMonoidです. AllはどちらもTrueの時にTrueになります. 一方AnyはどちらかがTrueの時にTrueになるようなMonoidです. Allの単位元はTrue, Anyの単位元はFalseです.
newtype All = All { getAll :: Bool }
instance Semigroup All where
a <> b = All (getAll a && getAll b)
instance Monoid All where
mempty = All True
newtype Any = Any { getAny :: Bool }
instance Semigroup Any where
a <> b = Any (getAny a || getAny b)
instance Monoid Any where
mempty = Any False
>>> getAll (All True <> mempty <> All False)
False
>>> getAny (Any True <> mempty <> Any False)
True
Sum, Product
Sum, Productはそれぞれ数字の足し算・掛け算についてのMonoidです.
newtype Sum a = Sum { getSum :: a }
instance Num a => Semigroup (Sum a) where
a <> b = Sum (getSum a + getSum b)
instance Num a => Monoid (Sum a) where
mempty = Sum 0
newtype Product a = Product { getProduct :: a }
instance Num a => Semigroup (Product a) where
a <> b = Product (getProduct a * getProduct b)
instance Num a => Monoid (Product a) where
mempty = Product 1
>>> getSum (Sum 1 <> Sum 2 <> mempty)
3
>>> getProduct (Product 3 <> Product 4 <> mempty)
12
Min, Max
これらはそれぞれ, 2つのうちの小さい方, 大きい方をとるという演算をするものです. 考えてみると最小値や最大値がないという場合, つまり単位元がない場合があるので, MonoidではなくSemigroupまでにしかならないことがわかります。
newtype Min a = Min { getMin :: a }
instance Ord a => Semigroup (Min a) where
a <> b = Min (getMin a `min` getMin b)
newtype Max a = Max { getMax :: a }
instance Ord a => Semigroup (Max a) where
a <> b = Max (getMax a `max` getMax b)
>>> getMin (Min 1 <> Min 4 <> Min 2)
1
>>> getMax (Max 'a' <> Max 'd' <> Max 'b')
'd'
Maybe
Maybeは, ある値xをもっているか(Just x), 何も値がないか(Nothing)どちらかを表すことができます. じつはSemigroupのインスタンスの値をMaybeにくるむことでMonoidの値にできます. 次のコードはその実装です. Nothingを単位元として扱い, どちらもJustなら内部のSemigroupの値を<>でくっつけていることがわかります.
data Maybe a
= Nothing -- 何もない
| Just a -- ある値を持っている
instance Semigroup a => Semigroup (Maybe a) where
Nothing <> x = x
x <> Nothing = x
Just x <> Just y = Just (x <> y)
instance Semigroup a => Monoid (Maybe a) where
mempty = Nothing
>>> Just (Min 4) <> Just (Min 2) <> Nothing
Just (Min 2)
>>> Just (Sum 1) <> Just (Sum 5) <> Nothing
Just (Sum 6)
実際にMonoidを活用してみる
最後にMonoidを使ったコードを見ていきましょう.
以下のコードは, 僕が@drkenさんの典型的な DP (動的計画法) のパターンを整理 Part 1 ~ ナップサック DP 編 ~の中にあるコードをHaskellに移植していた時のものです.
今回は, 部分和問題を扱ってみます. 流れとしてはDPテーブルを論理和をとりながらどんどん埋めていく感じで, 手続き的に書きました.
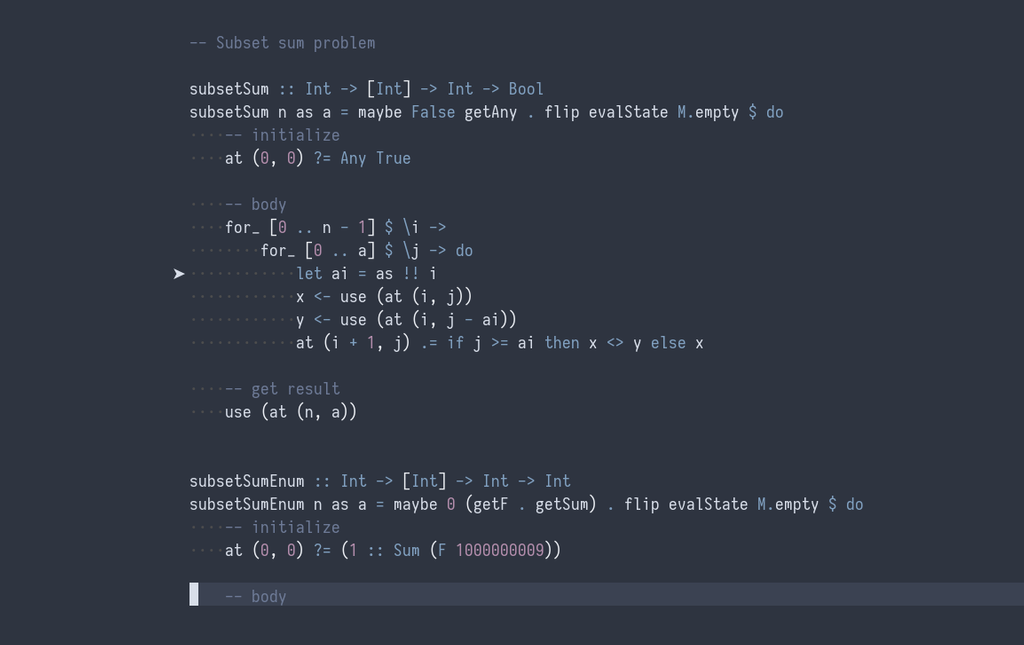
-- 部分和問題
subsetSum :: Int -> [Int] -> Int -> Bool
subsetSum n as a = maybe False getAny . flip evalState M.empty $ do
-- 初期条件
at (0, 0) ?= Any True
-- メインループ
for_ [0 .. n-1] $ \i ->
for_ [0 .. a] $ \j -> do
let ai = as !! i
x <- use (at (i, j))
y <- use (at (i, j-ai))
at (i+1, j) .= if j >= ai then x <> y else x
-- 最終結果を取り出す
use (at (n, a))
論理和をとるためにAnyMonoidを使ってみました. 普通に論理和を計算せずにMonoidを使うことには以下の利点があります.
Maybeの処理を<>に押し付けられる.- テーブルの初期化を少なくできた.
- 似たような手続きの計算を同じものとして扱うことができる.
1. Maybeの処理を<>に押し付けられる
x <- use (at (i, j))
y <- use (at (i, j-ai))
の行では, x,yにインデックスで示されたテーブルの中の値を束縛しています. しかし, そのインデックスが存在しない場合があるので, その値はMaybeにつつまれて返ってきます. もしテーブルの値が普通のBoolだった場合, 論理和を計算するためにはパターンマッチをしてMaybeをはがす必要があり, コードが複雑になってしまいます.
case (x, y) of
(Nothing, u) -> u
(v, Nothing) -> v
(Just u, Just v) -> Just (u || v)
今回は処理している値が2つだからまだいいですが, もっと多くなったとしたら...ぞっとしますね. ここでMaybeの上述したMonoidの性質を使うことを考えます. 論理和をとるためにAnyMonoidを使えば, さっきのコードが下のようになりました!
x <> y
いい感じですね. 複数個の値を計算するときも普通に書くことができます. さらにmconcatを使うことで, リストを<>でたたみこむというような処理ができるようになります. このようにMaybeの処理を<>にまかせることで, きれいになるだけでなく, できる処理の幅を増やすことができます!
2. テーブルの初期化処理を少なくできた
at (0, 0) ?= Any True
この行ではテーブルに初期条件の値を挿入しています. 本来なら, このように初期化する必要がありました.
at (0, 0) ?= Any True
for_ [1 .. a] $ \j ->
at (0, j) ?= Any False
このようにできたのは, Any FalseがAnyMonoidの単位元だからです. 先ほどあったように, テーブルの中の値はMaybeにつつまれて返ってきますが, その包まれた値がMonoidの単位元だった場合, それはMaybeMonoidの単位元Nothingと同じだと考えることができます.
Just mempty <> Just x = Just (mempty <> x) = Just x
Nothing <> Just x = Just x
したがって, 初期化でテーブルに単位元を入れても入れなくても結果的には同じ計算をしていることになります. このことから, 初期化を省くことができました. いつも省略できるとは限りませんが, MonoidをMaybeでくるんだときの単位元の挙動については, もしかしたら他の場面で使えるかもしれません.
3. 似たような手続きの計算を同じものとして扱うことができる
紹介したページ中には, 部分和問題の応用として部分和数え上げ問題がありました. それもHaskellで書いてみました. 余りを考えるので有限体Fを使い, 足し算をSumMonoidを使って埋め込んでいます.
-- 部分和数え上げ問題
subsetSumEnum :: Int -> [Int] -> Int -> Int
subsetSumEnum n as a = maybe 0 (getF . getSum) . flip evalState M.empty $ do
-- 初期条件
at (0, 0) ?= (1 :: Sum (F 1000000009))
-- メインループ
for_ [0 .. n-1] $ \i ->
for_ [0 .. a] $ \j -> do
let ai = as !! i
x <- use (at (i, j))
y <- use (at (i, j-ai))
at (i+1, j) .= if j >= ai then x <> y else x
-- 最終結果を取り出す
use (at (n, a))
部分和問題のコードと見比べてみるとほとんど同じことがわかります. 違うところは, 初期化の部分と最後のMaybeやMonoidをはがす部分です. 考えてみると, 2つの問題は求めたい値が違うだけで, 手続きとしては同じです. そこで論理和、足し算などの値の計算を<>に任せると, 同じものとして扱うことができます. したい計算に合わせてMonoidを取り換えて入れてあげることで, さまざまな計算ができることがわかりました!
おわりに
今回紹介した以外にもたくさんのMonoidやSemigroupがData.Monoid, Data.Semigroupで定義されています. 興味を持った人は戯れてみるとおもしろいと思います.
誤字・脱字・間違い, その他コメントがありましたら記事下部のコメント欄までご連絡ください.
明日はshirodoniさんの記事です. お楽しみに!