これは traP Advent Calendar 12月25日の飛び入り記事です.
はじめまして,幽霊のtobiomです.
今日はクリスマスですが,皆様どうお過ごしでしょうか.
さて突然の本題ですが,この記事ではクリスマスと全く関係なく私が最近勉強している Young図形 と呼ばれる図式を紹介していきます.
Young図形は100年ほど前にイギリスの数学者 Alfred Young が導入した図式で,現在では組み合わせが絡んだ表現論でよく用いられています.
物理ではなどLie群におけるテンソル積の既約分解を機械的に実行するためのツールとして使われたりしています.[1] [2]
記事の本編はこの文章の下に貼ってあるリンク先のpdfに書きました.
何も考えずに書くと硬い文章になりそうだったので,可能な限り人に読ませる文章と意識して書いたつもりです(それでも読みにくい文章だったらごめんなさい).
尚,本編をpdfで書いたのはYoung図形をmarkdownで出そうとすると一々画像で入れる必要があって面倒だったからです.
TeXを使うとytableau.styをプリアンブルに\usepackageで入れるだけでYoung図形をコマンドで以下のように簡単に書くことが出来たりします.[3]
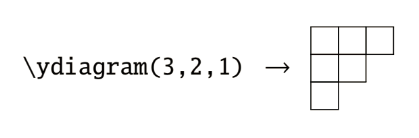
ここまでYoung図形について書いてきましたが,時間の都合上書けなかったことや私自身の理解不足もあって個人的には不完全燃焼のままなので,時間をみつけてpdfの本編をもっと盛りたいなあとか思ってます.
あと今回の記事を書いて代数をやるモチベがくらい生じた気がします.
最後に,ここまで読んでくださりありがとうございました.
とうとう12月25日になってしまいましたね.
明日の記事はあるんでしょうか.
例えばスピン同士の合成はスピン1重項とスピン3重項に分解できますが,これはでの直積を既約分解していることに相当します. ↩︎
本当はこのことについてもpdfに載せたかったのですが,のんびりやってたら時間足りなくなりました(許して). ↩︎
Young図形以外にも,自動的に大きさを調整してくれるブラケット記法のpackage(braket.sty),物理で使う記号などが使いやすい形で纏まったpackage(physics.sty),疑似コードの記述スタイルが入ったpackage(algorithms.sty)などTeXのpackageには数式が出てくる文章を書くのに便利なpackageが多数存在します. ↩︎
