This article was written for †rap Advent Calender 2017.
Tommorow's writer are neg(CDジャケットイラストメイキング) and uynet(FutureBass).

Doc2Vec

モチベーション

自然言語処理で文章の特徴量を使いたいタスク(SentimentAnalysis, 記事のレコメンド等)がある.

文章や文や段落(全て非固定長)単位で分類やクラスタリングをしたい
↓
教師有り/無し学習の手法のほとんどは, 入力となる特徴量が固定長であることを要求
↓
文章や文や段落の特徴量を, 統一的に求める手法が欲しい
↓
Bag of Words, Bag of Ngram, Doc2Vec

Word2Vec

Doc2Vecのモデルを説明する前に, 原型(Doc2VecはWord2Vecとほぼ同じとなったWord2Vecについて説明する.

Word2Vecとは単語の分散表現(単語一つ一つに対して有限次元のベクトル)を学習する手法の総称である. 記号である単語を線形空間に写すので, Word Embeddingとも呼ばれている.

Word2Vecによって得られた写された空間では, 単語の意味(ここで言う意味とはプログラム意味論に出てくるような数理論理学的に形式化されたものではなく, 自然言語に置ける我々が普段, 単語に対して持っている曖昧なものを指している)の近さが, 単語同士の距離に反映されている.つまり, "強い"や"強固", "頑丈"等の単語は空間上で近くに存在し, 逆に"弱小"や"弱い"等のの単語は遠くに存在するという意味である.

Word2Vecは教師なし学習として位置付けられており, その学習には文章が必要となる. ここで言う文章とは我々が日々SNSに書きなぐっているような短文でもいいし, 夏目漱石の小説全体としてもいい.

さて, 記号である単語を実数のベクトルに変換する最も簡易な方法を考える. 今注目している単語の語彙数がnである場合、その単語はn次元のone-hotベクトルで表現できる. one-hotベクトルとは次のように定義される.

注目している単語のリスト $[w_{0}, w_{2}, . ., w_{n - 1}]$ がある.
単語 $w_{i}$ は, i番目だけが1でそれ以外が0のn次元ベクトルで表現される(OneHot).

v_{w_{1}} = (1, 0, 0, . ., 0) v_{w_{2}} = (0, 1, 0, . ., 0) . . ., v_{w_{n}} = (0, 0, 0, . ., 1)

ここまでは一般的な単語のベクトル表現であり, これ自体がWord2Vecによって得られる分散表現では無い(1が立っている部分はソートの結果であり単語の意味などには全く関係していない上に, そもそもこれでは全てのベクトル同士のコサイン類似度(後述)は0であるため, 全ての単語が一様に似ていないという解釈しか出来ない).

そこで実際に分散表現を獲得する方法を見ていくのだが, Word2Vecの学習には文章が必要となる. そこで例として次の"私はお腹が減ったからとてもたくさんご飯を食べたい"を使用する. 今我々が議論している対象の最小構成要素は単語であるが, 我々の使用している日本語は英語等と違い単語単位での分かち書きがされていない. そのため, まずこれらを形態素解析によって単語単位に分割する必要がある.
形態素解析ソフトの一つであるMeCabを用いて上記の文を分割した結果、次のような単語のリストが得られる.

['私', 'は', 'お腹', 'が', '減っ', 'た', 'から', 'とても', 'たくさん', 'ご飯', 'を', '食べ', 'たい']

ここでこれは単語の集まりではなく, 単語がある順に沿って並んでいるリストであることに注目してもらいたい. これは, 文章というのは単なる単語の集合ではなく, 単語が出現する順序によってその意味が変わってくるものであり, またWord2Vecを初めとする様々な自然言語処理の技術ではこの単語の並びを重要な情報として手法に取り入れることによって, 精度の向上に寄与させている.
さて, ここでN-gramという概念を導入しよう. これは文字列や単語の列に対する概念で, 形式的には隣り合う単語で構成される長さNの部分列の集合である.
例を見てみよう. 上記の単語リストに対する2-gramだと, 次のようになる.

'私', 'は'
'は', 'お腹'
'お腹', 'が'
'が', '減っ'
...

Word2VecはこのN-gramの最後の単語(暫時的にTargetと呼ぶ)に対して, それ以前の単語の集合(これは一般的にContext, 文脈と呼ばれる)を用いる.
具体的には, Contextを用いてTargetを予測する際の, 単語の埋め込み行列 $W$ を学習することによって, 単語の埋め込み行列の各列ベクトルを, 単語の分散表現とするものである.

では, 単語の埋め込み行列とはどういうものであろうか？

ここで上記で説明したone-hotベクトルを用いて, 単語の埋め込み行列を見ていく.

ニューラルネットの内部では, 現実の情報は有限次元のベクトルで表現される. ここでは単語を考えているので, 先ほど言及したone-hotベクトルが内部表現として妥当であると思われる.
しかし, 既に言及したように, 次元が語彙数と等しい非常にスパースなベクトルは単語の表現として相応しくなく, そもそも計算量の面で非現実的である.
そこで, 一般的には次のような埋め込み行列 $W$ を考え, それを使って内部表現に変換する方法を考える.

v^{'}_{w_{i}} = W v_{w_{i}}, W = (e_{1}, e_{2}, . ., e_{n}), v_{w_{i}} = (0, . . ., 0, 1, 0, . ., 0)^{T}, v^{'}_{w_{i}} = e_{i}

ここで $e_{i}$ は列ベクトルであり $T$ はベクトルの転置である.

なぜ $v^{'}_{w_{i}} = e_{i}$ が成り立つのであろうか？例として $W v_{w_{1}}$ を書き出すと以下のようになる.

W v_{w_{1}}

=

(e_{1}, e_{2}, . ., e_{n}) v_{w_{1}}

=

⎝ ⎜ ⎜ ⎜ ⎜ ⎛ e_{11} e_{21} ⋮ e_{m 1} e_{12} e_{22} ⋮ e_{m 2} . . . . . . . . . . e_{1 n} e_{2 n} ⋮ e_{m n} ⎠ ⎟ ⎟ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ v_{w_{11}} v_{w_{12}} ⋮ v_{w_{1 n}} ⎠ ⎟ ⎟ ⎟ ⎟ ⎞

=

⎝ ⎜ ⎜ ⎜ ⎜ ⎛ e_{11} e_{21} ⋮ e_{m 1} e_{12} e_{22} ⋮ e_{m 2} . . . . . . . . . . e_{1 n} e_{2 n} ⋮ e_{m n} ⎠ ⎟ ⎟ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ 10 ⋮ 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎞

=

⎝ ⎜ ⎜ ⎜ ⎜ ⎛ e_{11} e_{21} ⋮ e_{m 1} ⎠ ⎟ ⎟ ⎟ ⎟ ⎞

=

e_{1}

つまり $W v_{w_{i}}$ は $W$ の $i$ 番目の列ベクトルを取り出すのである(これは一般的にはlookupと呼ばれる). そしてこれこそがニューラルネットの内部表現となるのである( $m$ は分散表現ベクトルの次元である).

なぜこのようにわざわざ $W$ を用いて内部表現を定義するのか?
重要なのは, この $W$ というのはone-hotベクトルに対する線形変換となっており, つまりNNのパラメータであるということだ. NNのパラメータであるというのは, これらのパラメータを使用して計算された結果を用いて計算される誤差によってパラメータの最適化ができるということである.
つまり, このような上のような内部表現への変換を定義することによって, 学習可能なパラメータ自体を単語の分散表現として扱うことができるようになるのである.

さて, それではどのように誤差関数を計算するのだろうか?これは上で述べたN-gramのTargetをContextによって予測する際の誤差を使用することになる.

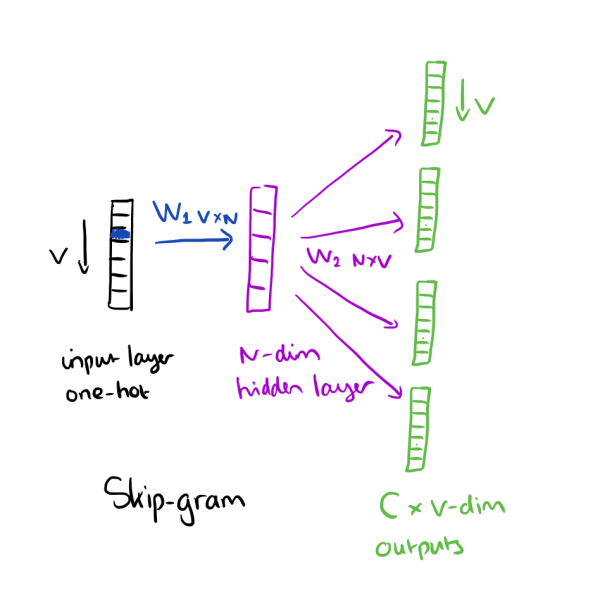
誤差を計算する際, NNのモデルは次のようになる.

e r r o r = c r o s s e n t r o p y (y_{t r u e}, y)

y = s o f t m a x (y^{'})

y^{'} = U x + b

x = c o n c a t ([v^{'}_{w_{c o n t e x t 1}}, v^{'}_{w_{c o n t e x t 2}}, . .])

o r

x = a v e r a g e ([v^{'}_{w_{c o n t e x t 1}}, v^{'}_{w_{c o n t e x t 2}}, . .])

[c o n t e x t 1, c o n t e x t 2, . ., t a r g e t,] \in N G r a m O f (D o c u m e n t_{i})

y_{t r u e} = v_{t a r g e t}

ここで $x$ は分散表現の連結又は平均である(分散表現ベクトルの次元mは同じなので, 平均は要素ごとに取る).
$U$ は, 連結の場合, $m \times (c o n t e x t のサイズ)$ 次元ベクトルから語彙数次元ベクトルへの変換行列で, 平均の場合, $m$ 次元ベクトルから語彙数次元ベクトルへの変換行列である.

この $e r r o r$ を最小化するようにパラメータ最適化を行っていく中で, $W$ が学習され, 結果としてその各列ベクトルが単語の分散表現に相当する.

なお, ここで言語モデルでは, 分散表現に対して変換行列 $U$ を使用しているが, 分散表現同士の内積が指数関数の肩に乗った $e x p (φ (v_{w_{i}}, v_{w_{j}}))$ を用いる双線形対数モデルを採用する場合もある.

Doc2Vec

ここでようやくDoc2Vecの話が可能となる. 実のところ, Doc2Vecと前節のWord2Vecの違いはほんの少しである.

先ほど, 単語の分散表現を得るために, $W$ という単語の埋め込み行列を考えた. そこで天下り的だが, 同じく文章の埋め込み行列 $D$ を考える. $W$ と同様に各列ベクトルが文章の分散表現に相当する.

注目している文章で構成されるリスト $[d_{0}, d_{2}, . ., d_{n - 1}]$ がある.

D = (s_{1}, s_{2}, . ., s_{m})

v_{s_{i}} = (0, . . ., 0, 1, 0, . ., 0)^{T}

v^{'}_{s_{i}} = s_{i}

埋め込み行列 $D$ は単語の場合と全く同様の議論によって各列が文章の分散表現ベクトルに相当するのは最早自明であろう.

Word2Vecと本質的に違うのは, あるN-gramのTargetをContextで予測する場合に, 文章の分散表現も使用するという点である.

つまり, 文章 $i$ 中のN-gramの各Targetを予測する際, Contextの単語集合に加え, 文章 $i$ の分散表現も同時に使用するのである. これは形式的に次のように書ける.

e r r o r = c r o s s e n t r o p y (y_{t r u e}, y)

y = s o f t m a x (y^{'})

y^{'} = U x + b

x = c o n c a t ([v^{'}_{w_{c o n t e x t 1}}, v^{'}_{w_{c o n t e x t 2}}, . ., v^{'}_{D o c u m e n t_{i}}])

o r

x = a v e r a g e ([v^{'}_{w_{c o n t e x t 1}}, v^{'}_{w_{c o n t e x t 2}}, . ., v^{'}_{D o c u m e n t_{i}}])

[c o n t e x t 1, c o n t e x t 2, . ., t a r g e t,] \in N G r a m O f (D o c u m e n t_{i})

y_{t r u e} = v_{t a r g e t}

つまり, $x$ 計算する際に連結であろうが平均であろうが, 文章の分散表現を予測に影響させる, という点がポイントである.

注意する点として, 全ての文章の分散表現を学習について, 単語の埋め込みベクトルは共有されるという点である. つまり, 文章ごとに単語の埋め込みベクトルを学習するのではなく, 全ての文章を一斉に学習するのである. つまり, 単語の埋め込みベクトルはアルゴリズムの一番外側でfixされているということである.

さて, このようにして得られる文章の分散表現はPV-DM(Paragraph Vector Distributed Memory)と呼ばれる.
Doc2Vecでもう一つの計算によって得られる分散表現がある. これは, 文章の分散表現のみを使って, 文章中の単語を予測するというモデルの学習によってパラメータを最適化する手法である. この場合, PV-DMと違い, 単語のN-gramを完全に無視して文章ごとの単語の出現しやすさを学習していることになる. こちらは1つの入力(つまり分散表現)から文章中に出現する単語全てを, その出現頻度を考慮した学習していることになる. この計算で得られる文章の分散表現はPV-DBOW(Paragraph Vector Distributed Bag of Words)と呼ばれる.

応用上, PV-DMのみでも高い性能を達成することが出来るが, PV-DBOWと連結(concat)したものを文章の素性(分散表現)とすることでさらに性能が改善されることが知られている.

Gensim

さて, 上記に示したDoc2Vecの計算方法であるが, Gensimという自然言語処理ライブラリに実装されている. KerasやChainer等でこれらを実装することは可能(双線形対数モデルを採用しない場合は単なる1層NNとなるので非常に容易)だが, 実務上の分析ではGensimを用いるべきである.

さて, 必要なライブラリをインストールするところから始めよう. なお, ここからは作業用のディレクトリworkを作成して, そこで全ての作業を行うことにする.

まずはmacOSの場合に関して.

brew install mecab mecab-ipadic wget
pip install gensim mecab-python3

これでgensimと形態素解析ライブラリであるMeCabがインストールされるはずである.

次にWindowsの場合だが, 残念だがwindowsでMeCabをインストールするのは難しく, sourceからビルドするしかないのだが, makefileの書き換えやコードのtypoの修正等の非常に煩雑な作業となり本記事の扱うところを超えてしまうため, 代わりの形態素解析ライブラリを用いる必要がある. またtarコマンドの代りに, tarファイルを解凍するソフトを入手する必要がある.

7zip

pip install gensim janome

こちらのjanomeはpythonでpureに実装されているため問題なくインストールできるはずである.

それでは、ライブラリの準備ができたので, 実際にDoc2Vecで記事データを学習していく.

まずは学習に必要なデータをダウンロードする. livedoorのニュースコーパスから記事を用いることにする. macOSの場合だ.

$ wget http://www.rondhuit.com/download/ldcc-20140209.tar.gz
$ tar xvfz ldcc-20140209.tar.gz

Windowsの場合だが, http://www.rondhuit.com/download/ldcc-20140209.tar.gz を直接ブラウザに入力するとファイルがダウンロードされる. それを解凍してworkに配置する.

Doc2Vecで文書を学習させるコードを書いていく. まずは必要ライブラリをimportする. ここはOSによってjanome又はMeCabどちらかのみをimportすれば良い.

import sys
from os import listdir, path

from gensim import models
from gensim.models.doc2vec import LabeledSentence

import MeCab
from janome.tokenizer import Tokenizer

次に, 記事ファイルをダウンロードしたディレクトリから取得する関数を定義する.

def corpusFiles():
    dirs = [path.join("./text", x) for x in listdir("./text") if not (x.endswith(".txt") or x.startswith(".DS"))]
    docs = [path.join(x, y) for x in dirs for y in listdir(x) if not (x.startswith("LICENSE") or x.startswith(".DS"))]
    return docs

その次は, 記事コンテンツをパスから取得する関数を定義する.

def readDoc(path):
    with open(path, "r") as f:
        return f.read()

MeCab又はjanomeを使って記事を単語リストに変換する関数を定義する. なおここは自分のOSに合わせてすること.

def split2Words_mecab(text):
    parser = lambda x: MeCab.Tagger("-Owakati").parse(x).split(" ")
    return parser(text)

def split2Words_janome(text):
    t = Tokenizer(wakati=True)
    tokens = t.tokenize(text)
    return tokens

次に, 記事コンテンツを単語に分割して, Doc2Vecの入力に使うLabeledSentenceに変換する関数を定義する. なおここも自分のOSに合わせてすること(ここではjanomeの方を選択している).

def doc2Sentence(doc, name):
    # words = split2Words_mecab(doc)
    words = split2Words_janome(doc)
    return LabeledSentence(words = words, tags = [name])

これらの関数を組み合わせて記事のパスリストから, 記事コンテンツに変換し単語分割して, センテンスのジェネレーターを返す関数を定義する. なぜジェネレータかというと, 大規模な文章集合を訓練する際はメモリに全てのデータが乗らないためである.

def corpus2Sentences(corpus):
    docs = [readDoc(x) for x in corpus]
    for i, (doc, name) in enumerate(zip(docs, corpus)):
        sys.stdout.write("\rPre-Processing Now... {}/{}".format(i, len(corpus)))
        yield doc2Sentence(doc, name)

では最後にDoc2Vecパラメータを渡して学習させる.

if __name__ == "__main__":
    corpus = corpusFiles()
    sentences = corpus2Sentences(corpus)

    model = models.Doc2Vec(sentences,
                           dm = 1,
                           size = 300,
                           window = 15,
                           alpha = .025,
                           min_alpha = .025,
                           min_count = 1,
                           sample = 1e-6)

    print("\n訓練開始")
    for epoch in range(20):
        print("Epoch: {}".format(epoch + 1))
        model.train(sentences, total_examples = model.corpus_count, epochs = model.iter)
        model.alpha -= (0.025 - 0.0001) / 19
        model.min_alpha = model.alpha

ここでmodels.Doc2Vecの引数を説明しよう.

dm: 1の時はPV-DMを学習, それ以外の場合はPV-DBOW.
size: 分散表現の次元数.
window: N-gramのNのサイズ.
alpha: 学習率
min_alpha: 最低学習率. 学習率はこのモデルではこれ以上下がらない.
min_count: 出現回数がmin_count以上のものだけ単語としてとる.
sample: downsampling, つまり接続詞等の非常に頻繁に出現する単語を無視する確率である.

モデルの保存以下のようにして, saveメソッドにファイル名を指定する(上記のコードに最後にモデルを保存すること).

model.save("doc2vec.model")

さて, ここまでのコードをlearning.pyという名前でworkに保存し, 実行する.

python learning.py

では次に学習されたモデルを使って遊んで見よう. 今までと同じようにworkでの作業を仮定する.

importするライブラリとディレクトリから.txtファイルへのpathを列挙する関数は先ほど言及したので単に次のようにする.

import sys
from os import listdir, path

from gensim import models
from gensim.models.doc2vec import LabeledSentence

import MeCab
from janome.tokenizer import Tokenizer

def corpusFiles():
    dirs = [path.join("./text", x) for x in listdir("./text") if not (x.endswith(".txt") or x.startswith(".DS"))]
    docs = [path.join(x, y) for x in dirs for y in listdir(x) if not (x.startswith("LICENSE") or x.startswith(".DS"))]
    return docs

まずは先ほどsaveしたモデルをloadしよう.

model = models.Doc2Vec.load("doc2vec.model")

次に適当に二つ文章を持ってきて, どれくらい似ているか調べて見よう. なお, 分散表現の類似性を測るには, 分散表現はベクトルであるため一般的にはコサイン類似度を使う. この量は似ていれば1に近付き, 違っていれば0に近付く量である. 詳しくは次の記事を参照すること.

コサイン類似度について

sim = model.docvecs.similarity('./text/livedoor-homme/livedoor-homme-4700669.txt', './text/movie-enter/movie-enter-5947726.txt')
print(sim)

では次に全ての文章に対する分散表現をnumpy配列として得る方法を見る. Gensimが提供するgensim.models.doc2vec.DocvecsArrayクラスのインスタンスは, 学習時にLabeledSentenceのtagに渡した[name]ファイル名でのnameをkeyとするdictのようなものを提供するため, ファイル名をもう一回取得し, アクセスすれば良い. なお, ここから分類器へ入力する特徴量として使う際は, これらを保存すれば良い.

corpus = corpusFiles()
for i in corpus:
    print(i, model.docvecs[i])

Reference

Python で「老人と海」を word2vec する

Doc2Vecの仕組みとgensimを使った文書類似度算出チュートリアル

models.doc2vec – Deep learning with paragraph2vec

Janome v0.3 documentation (ja)

Python3で形態素解析エンジンMeCabを使えるようにする(2016年3月版)

Distributed Representations of Sentences and Documents

文章をよしなに分散表現しよう

Doc2Vec

目次

モチベーション

Word2Vec

Doc2Vec

Gensim

Reference

関連する記事

文章をよしなに分散表現しよう

Doc2Vec

目次

モチベーション

Word2Vec

Doc2Vec

Gensim

Reference

この記事をシェア

関連する記事