皆さんこんばんわ。Davidです。
今(12/26 01:01)この記事を書き始めたワケですが、実は12/24の投稿だったんですね〜。
いやホント申し訳ない。なぜかクリスマス・イブなら僕はassignされてないだろうとか言う妙な思い込みがあったんですね。申し訳ない。

はい、という訳で、一応書いていくんですけども、今回はRustでMCMCの一手法である、Metropolis-Hasting(M-H)法を書きました。

皆さんMCMCってご存知ですか？
もちろん、MiッCuMi〜Cuにし〜てやんよ〜のMCMCではありません。
Marcov Chain Monte CarloのMCMCです。

さて、すでに講義で数値計算を履修した人なら知ってることですが、Monte Carlo(法)というのは、何か計算したいものを、乱数を使ってゴリゴリ近似していく計算方法です。オーソドックスなのだと、円周率の計算を$r_1\sim U(0,1),r_2\sim U(0,1)$を満たすようなサンプルから計算するやつとかですかね！

MCMCもMonte Carlo法の一種です。ではこれは一体、何を計算するためのモノなのでしょうか？
それはある確率分布$P$に従うサンプルを計算するための技法です。

一つ例を上げましょう。確率分布に関しては大丈夫ですね？これはナイーブには、あるドメインDがあって、そのドメインの要素それぞれに対して実数(確率)を返す関数です。確率なので、全ての要素に対応する確率の総和は1.0となります。型を書くと、$P::D\to R$となります.

今、我々にはある確率分布$P$が与えられており、それを使い任意の要素$x\in D$に対する確率または正規化されていない確率は計算できるとしましょう。問題は、&P&に従うようなサンプルxの多重集合を計算しなさい、というものになります。

これってどうやって計算するんでしょうか？

逆関数を求めて、確率からサンプルを求めればいいじゃないか！というのはあります。しかし厳密には、全単射じゃないと逆関数が定義できないので、そこからだけでも一部の分布にしかこの考え方による手法が適用できないことわかります。
また、実際に逆関数が存在することと、それを構成する難しさは別で、$U(0,1)$に従うサンプルを求めたい分布に従うサンプルに写す関数を、確率分布の定理を使い積分をかますことで構成することができます。が、これは一般的な変な形をした複雑な分布に対しては、解析に求めることは難しすぎて、できません。

そこで、我々にはもっと一般的なサンプリング手法が必要になるのですが、一変数の分布に対しては効率的にサンプリングできるアルゴリズム(棄却サンプリング等)や、サンプルを得る訳ではなくサンプルを使って計算するアルゴリズム(重点サンプリング(サンプリングってついてるのにちょっと違うんだなこれが))はあるのですが、サンプルが多次元の場合にそれらの手法を適用しようとすると、色々問題が出てきます。まぁほぼ次元の呪いが悪いんですけどね。

なので、一般的な高次元のサンプルをサンプリングするアルゴリズムが必要になる訳ですが、その中で一つ大きな分野がMCMCになります。

MCMCはその名前の通り、Monte Carlo法なので乱数を使います。そしてまた、その名前の通り、Marcov Chain、マルコフ連鎖が裏の理論に大きく、重要な仕事をしています(なんかこの書き方英語っぽくてクサイですね)。

さて、今サンプリングした対象の分布を$P$とすると、MCMCでは、この$P$と共に、独立に選ぶことができる別の分布Qを使います。MCMCにおけるサンプリング過程の大雑把なキモを説明すると、各サンプルを$P$と遷移確率分布$Q$で計算される分布のマルコフ連鎖の系列とすることで、効率的にサンプリングを行う、というモノです。

なぜマルコフ連鎖が絡んでくるのでしょう？こいつは出来の悪い、2gramベースでの言語生成モデルにしか出てこない、HMMを説明するための概念上あったほうが嬉しい、くらいの道具では無かったのでしょうか(まぁ言語モデルはNNがさいっっきょうなのでHMMとかくらいじゃね...iHMMとかiTHMMとかのディリクレ過程系を持ってこないと脳筋さいつよNNにはちょっと勝てないからね)？

これを説明するには、不変分布と詳細釣り合い条件、そしてエルゴード性という三つの要素について話す必要があるのですが、長いので、以下に概要を示します。

1. 不変分布: あるマルコフ連鎖に対して定義される。マルコフ連鎖のあるステップでサンプリングされたサンプル$x$が分布$P$に従うなら、次のステップでサンプリングされる$x^{\prime }$も分布$P$に従うような、マルコフ連鎖が持つ。これ持っているマルコフ連鎖は不変であるとか、定常であるとか言う。
2. 詳細釣り合い条件: これを満たすような$P$と$Q$があれば、(1)を持つマルコフ連鎖が作れる.
3. 任意の分布から始めたマルコフ連鎖が不変分布を持つことができる.

(1)はそれはそうって感じですね、$P$からサンプリングしたいわけですから、系列全体をサンプルの多重集合とするなら、系列のステップごとに$P$に従うようなサンプルがサンプリングされて欲しいですよね。
(2)は結構面白くて、これを満たせれば、そのマルコフ連鎖は不変になります。これは後々の手法が理論的に不変分布を持つための証明の随所で出てくるんですよ〜。
(3)もそれはそう。だって最初のサンプル点をどこに打てばわからないから、大体のマルコフ連鎖の系列の最初のステップの分布は$P$じゃなくておそらく裾の広い一様な分布ですよね。そこからご所望の$P$をマルコフ連鎖に持たせないといけない訳ですから。もっと感覚的には、サンプリング点の空間の一部にさえ近づきさえすれば、そこからいい感じに効率的にサンプリングできるので、最初の開始点がクソでも任意の点に動くことができれば、どうにかなるってことですかね。

はい。ここまで話しましたが、じゃあQってどうやって作るのさ？という話になりますね。そんな都合のいい分布そうそう無いんじゃ無イカ(注意: 筆者はSONY SIEに就職なのでイカはやってません。モンハンをやれ。プレステ最高FOOOOOO↑。なお同期達と人事は懇親会の紹介で皆イカを愛遊していることで盛り上がってたので特にそういう制約はありません)？という疑問は出てくるでしょうが、MCMCのすごいのは、任意の$Q^{\prime }$(解析的にサンプリングできて、かつ適当な遷移確率となりうる分布、例えば現在のサンプル点を平均とした標準偏差hogehogeの多次元正規分布)から、(2)を満たす$Q$を作るアルゴリズムが存在する、ということです。

今回私が実装したのは、M-H法です。

大まかには(眠くなってきた)$Q^{\prime }$から、$P$のサンプリング点、の候補点xをサンプリングします。その後、$P$と$Q^{\prime }$でxをPのサンプリング点として受理する確率を計算し、それに従って受理します。受理された場合は現在の点を更新し、次の点に映りますが、されなかったら現在の点はそのままでxを$Q^{\prime }$からサンプリングし、受理確率を計算し...をやり直します。

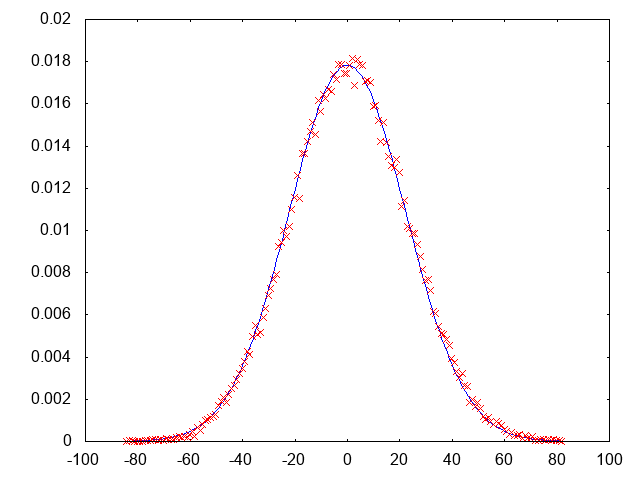
さて、流石に寝るのですが、結果を乗せて起きましょう。分散が500の10次元等方正規分布から70000点サンプリングしたサンプルの1次元目の要素のヒストグラム(赤)です。今回は等方なので、多次元ガウス分布に関する一般的な性質から、対応する周辺分布(ここではサンプルの1次元目に相当する変数が従う分布)は分散500に従います。それを確かめるために、すでに知られている計算することができる1変数ガウス分布のグラフ(青)を重ねて書きました。しっかりと合ってますね。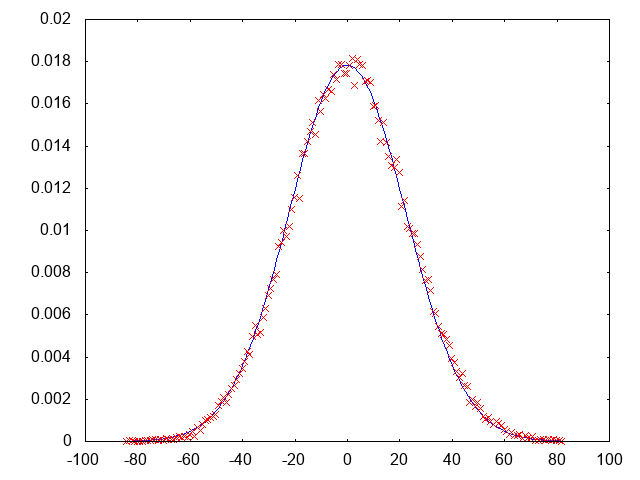

リポジトリを張っておくので、コードはこっから見て下さい。結構なRustっぽくなさなのでバンバン指摘くれると嬉しいです！

ちなみに今回Rustで書いたのは特に意味はなく、Rustの勉強のためです。ヒストグラムとか全部自分で書いたけど、結構書きやすくていいですねRust。Haskellみたいな気持ちで、より早い(というかC/C++と同じくらい?)のでガンガン機械学習に使えて良いですね。なおRustに関する記述はここの部分とタイトルだけです(は?)。

明日は誰がAdv書くんでしたっけ？
traP人が多すぎてよく覚えていないですね...修士の学位もらって終了したら、僕もOBか...なんか寂しくなりますね！

オンオンオン!!!!!!!!!

ではみなさん、良いお年を！Merry X'smas!過好新年!

References

PRML上
計算統計Ⅱ