はじめに

この記事は11月25日のAdC用の記事です。

どうも、幽霊部員のえんたんぐるです。この記事では、僕が最近勉強したこととして統計力学模型を用いた組みひも多項式の導出についてまとめたいと思います(誰得?)。単にまとめただけなので推論はガバガバで読めたものじゃありませんので、とりあえず結論だけ先に言っておきたいと思います:

Jones多項式を導いたJonesさんはすごいぞ。

結び目と組みひもについて

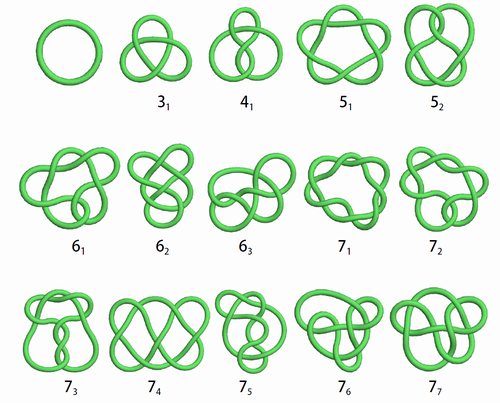
位相幾何学(topology)では、連続的な変換によって不変な性質を研究します。結び目(複数のひもからなる場合は絡み目)はまさにtopologyの対象です。これは3次元空間でひもを適当に絡ませた後両端を結んだものであり、ひもを切ること以外で自由に変形できます。

絡み目が与えられたら、それを分類したいと考えるのは自然です。一般に連続変換で不変な量を位相不変量(topological invariant)と呼び、絡み目の場合は絡み目不変量(link invariant),多項式として得られる場合は絡み目多項式(link polynomial)と呼びます。これをsystematicに求める方法について考えます。

全ての絡み目は組みひもとして(非一意的に)表すことができます。組みひもは、以下のように複数のひもを横に並べたものです。

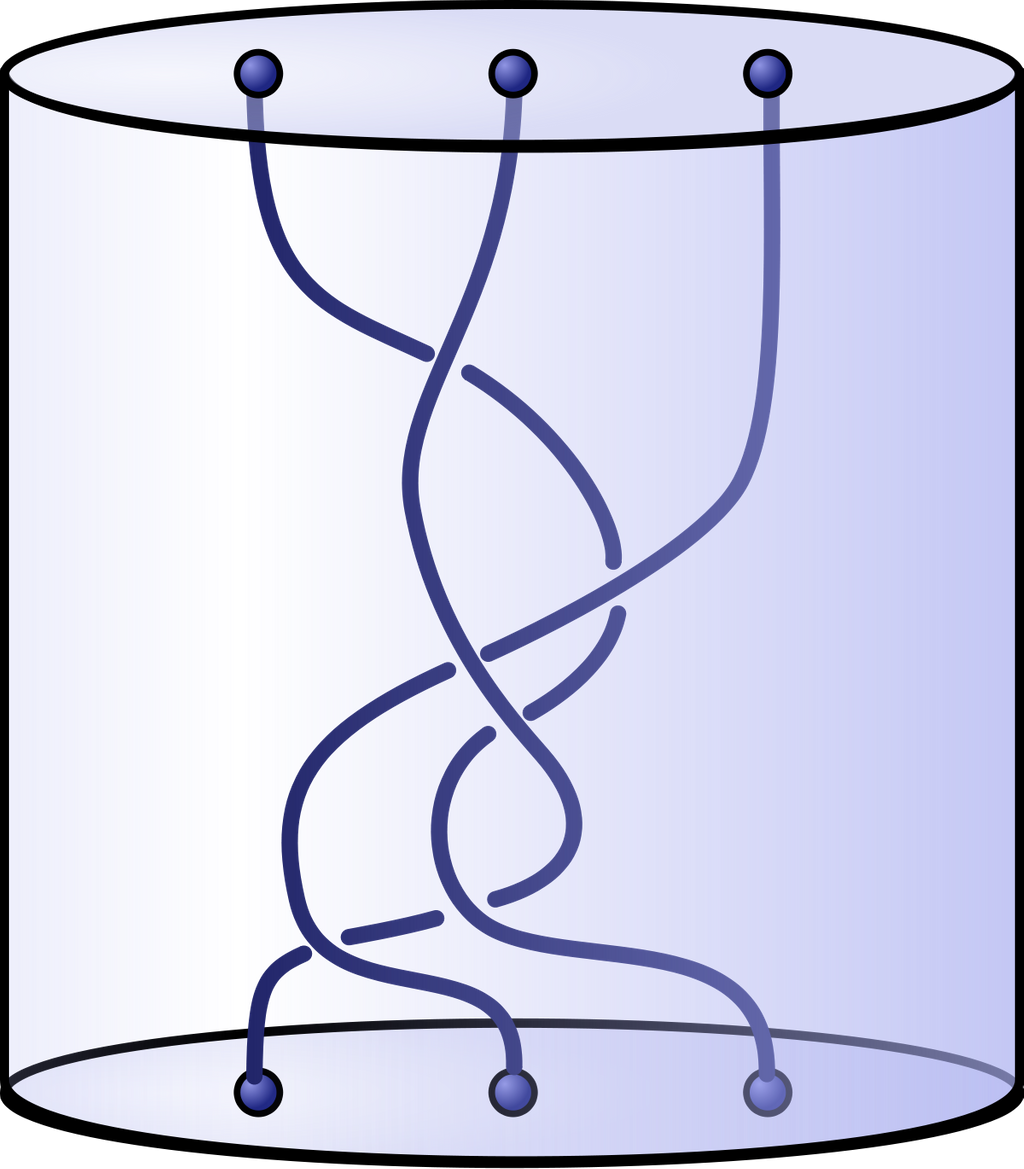
$i$番目のひもと$i+1$番目のひもを交差させる操作を$b_i,b_i^{-1}$とします。操作の積も定義します。

このとき、生成子$b_1,b_2,...,b_{n-1}$からつくられる組みひも群(braid group)${\mathcal{B}}_n$は次の関係式で定義されます。

$$b_i{b}_j=b_j{b}_i\left(\left|i-j\right|\ge 2\right)$$

$$b_i{b}_{i+1}{b}_i=b_{i+1}{b}_i{b}_{i+1}$$

演習(やんなくていいです):この関係式が成り立つことを確認せよ。

組みひもで向かい合った点をつなぎ、閉じた組みひも(closed braid)をつくると結び目や絡み目が作れます。前述したとおりこの表し方は一意ではありません。以下のMarkovの定理が成り立ちます。

markovの定理:

同じ絡み目を表す等価な組みひもは、次の2種の操作を有限回行うことによって互いに移り変わることができる。

$$AB\to BA(A,B\in {\mathcal{B}}_n)$$

$$A\to A{b}_n^{\pm 1}(A\in {\mathcal{B}}_n,b_n\in {\mathcal{B}}_{n+1})$$

絡み目多項式はMarkov操作によって不変なものと考えられるので、次の性質を満たす$\alpha (\cdot )$として定義されます。

$$\alpha \left(AB\right)=\alpha \left(BA\right)(A,B\in {\mathcal{B}}_n)$$

$$\alpha \left(A\right)=\alpha \left(A{G}_n^{\pm 1}\right)(A\in {\mathcal{B}}_n,G_n\in {\mathcal{B}}_{n+1})$$

ここで$G_i$は$b_i$の表現です。似たような性質を持つ量としてMarkov trace $\varphi (\cdot )$を定義します。

$$\varphi \left(AB\right)=\varphi \left(BA\right)(A,B\in {\mathcal{B}}_n)$$

$$\varphi \left(A{G}_n\right)=\tau \varphi (A),\varphi \left(A{G}_n^{-1}\right)=\overline{\tau }\varphi (A)(A\in {\mathcal{B}}_n,G_n\in {\mathcal{B}}_{n+1})$$

$$\tau =\varphi (G_n),\overline{\tau }=\varphi (G_n^{-1})$$

Markov traceが分かれば、絡み目多項式を以下のように構成することができます。(ここで$e(A)$は$A$の要素$b_i$の指数和,$A=b_1{b}_2^2{b}_1^{-1}$なら$e(A)=1+2-1=2$等)

$$\alpha (A)={\left(\tau \overline{\tau }\right)}^{-(n-1)/2}{\left(\frac{\overline{\tau }}{\tau }\right)}^{e(A)/2}\varphi (A)$$

演習(やんなくていいです):この$\alpha (\cdot )$が組みひも多項式となっていることを確かめよ。

よって、組みひも群の表現とMarkov traceを作ったら絡み目多項式が得られることが分かります。

統計力学におけるYang-Baxter関係

ここまで書いた時点でやる気が消失、おまけに予約投稿の制度も知らなかったので時間内にできずモチベーションが-$\infty$になりました。そもそも格子模型いまあんまりやる気なかったわ。

そんなわけでここから先は巻きでいきたいと思います。

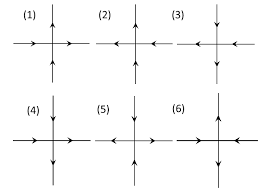
統計力学におけるvertex模型とは、2次元の正方格子の辺の上に状態変数を置いたものです。ここでは辺の上にスピンのような矢印が乗ってて、上向きとか下向き(横の辺なら右向き左向き)をとる模型を考えます。

このスピンの矢印はほかの矢印と相互作用をします。矢印を磁石として考えると、棒磁石の向きによってN極同士が近づくような配置だと反発しあってエネルギーが大きくなり、N,S極が近づく配置だとひかれあって安定しエネルギーが小さくなります。

ここで、エネルギーが大きいというのは状態が不安定であるということを言っています。物理系は基本的に安定な状態を好みますので、エネルギーが小さい状態を好みます。外部からエネルギーを与えたらその分のエネルギーを吸収して不安定な状態になったりしますが。

統計力学(の、カノニカルアンサンブル)では、平衡状態においてエネルギー$E_i$の状態が実現される確率を次のように表します。

$$p(E)=\frac{1}{Z}\sum _i\exp \left(-E_i/k_{B}T\right)$$

エネルギー$E_i$が小さい状態がほど実現されやすいのが分かります。これと同様に、格子模型の辺$i,j,k,l$に囲まれた頂点の統計重率を次のように定義します。

$$w(i,j,k,l)=\exp \left[-ϵ(i,j,k,l)/k_{B}T\right]$$

局所的なエネルギー$ϵ(i,j,k,l)$は$i,j,k,l$のそれぞれの矢印の配意によって変化します。考えられる配意として次の6つを考えます。これを6 vertex modelといいます。

$${ϵ}_1={ϵ}_2,{ϵ}_3={ϵ}_4,{ϵ}_5={ϵ}_6,{ϵ}_7={ϵ}_8$$

格子全体のエネルギー、分配関数(これ一個であらゆる物理量が得られるすごいやつ)、格子点あたりの自由エネルギー()は次のようになります。

$$E=\sum _{j=1}^6{n}_j{ϵ}_j$$

$$Z_N=\sum _{\{n_j\}}\exp \left[-E/k_{B}T\right]$$

$$f=-k_{B}T\underset{N\to \infty }{\lim }$$

そしてこういう問題のよくわからない量その1である転送行列を定義します。

$$T_{\alpha \beta }=\sum _{{\mu }_1}\cdots \sum _{{\mu }_n}w\left({\mu }_1,{\alpha }_1,{\mu }_2,{\beta }_1\right)w\left({\mu }_2,{\alpha }_2,{\mu }_3,{\beta }_2\right)\cdots w\left({\mu }_n,{\alpha }_n,{\mu }_1,{\beta }_n\right)$$

これは格子のある横一列に注目したとき、辺の下側の情報を上側に伝えるという操作をしています(無理して理解しなくていいです。)これを用いると分配関数を簡単に表すことができます。

$$Z_N=\sum _{{\varphi }_1}\sum _{{\varphi }_2}\cdots \sum _{{\varphi }_m}{T}_{{\varphi }_1{\varphi }_2}{T}_{{\varphi }_2{\varphi }_3}\cdots T_{{\varphi }_m{\varphi }_1}=\mathrm{T}\mathrm{r}{T}^m$$

ここで、頂点のエネルギーの情報を持っていた統計重率が、スペクトルパラメータ$u$なる情報を含んでいるとします。いまいちこの$u$の意味がよくわかりませんが、何かの固有値らしいなぁという感じです。勉強不足ですまぬ。(一応類似であるソリトンの例を考えるとこれは運動量の固有値みたいになってます。)

ところで、転送行列は実は保存量の母関数になっていて、これがことなる$u$に対して交換するという条件から全ての保存量が可換であることの条件が得られます。このときモデルを厳密に解くことができるようです。よってこの時の条件を

$$\left[T(u),T(v)\right]=0$$

と書くことができます。統計重率が次の関係式を満たすとき上の式を満たすことが示せます。

$$\sum _{\gamma {\mu }^{\prime \prime }{\nu }^{\prime \prime }}w\left(\mu ,\alpha ,{\mu }^{\prime \prime },\gamma ;u\right)w\left(\nu ,\gamma ,{\nu }^{\prime \prime },\beta ;u+\nu \right)w\left({\nu }^{\prime \prime },{\mu }^{\prime \prime },{\mu }^{\prime },{\nu }^{\prime };v\right)=\sum _{\gamma {\mu }^{\prime \prime }{\nu }^{\prime \prime }}w\left(\nu ,\mu ,{\mu }^{\prime \prime },{\nu }^{\prime \prime };v\right)w\left({\mu }^{\prime \prime },\alpha ,{\mu }^{\prime },\gamma ;u+v\right)w\left({\nu }^{\prime \prime },\gamma ,{\nu }^{\prime },\beta ;u\right)$$

これを格子模型におけるYang-Baxter関係式といいます。格子模型に限らずソリトンやらなんやらででてくるYang-Baxter関係式というのは、様々な状況において模型の可解性(Hamilton力学系における可積分性)を満たすための類似の関係式です。背景にある数理構造が同じのようです。

で、そんなYang-Baxter関係式が出てくる別の例を考えて、二つの例に出てくる同じ役割をしている量を同一視するという荒業をします。その例というのが相対論的な散乱の問題で、このときスペクトルパラメータ$u$は以下で示されるラピディティーという量になります。($u$が十分小さいときには速度と一致する)

$$E=m\cosh u,P=m\sinh u$$

n種の粒子があり、粒子iの状態を演算子$R_i^{†}(u)$で表します。演算子の交換関係からS行列(散乱行列)を定義します。

$$R_j^{†}(u_1)R_j^{†}(u_2)=\sum _{kl}{S}_{jl}^{ik}(u_{21})R_k^{†}(u_2)R_l^{†}(u_1),(u_1<u_2)$$

始状態が$R_k^{†}(u_1)R_j^{†}(u_2)R_i^{†}(u_3)$,終状態が$R_p^{†}(u_3)R_q^{†}(u_2)R_r^{†}(u_1)$で表される3粒子の散乱を考えます。散乱には[123]→[132]→[312]→[321]と[123]→[213]→[231]→[321]という2つの経路が考えられ、それらの結果が等価であるという条件から次のS行列についてのYang-Baxter関係式が導かれます。

$$\sum _{\alpha \beta \gamma }{S}_{j\beta }^{i\alpha }(u)S_{k\gamma }^{\alpha p}(u+v)S_{\gamma r}^{\beta q}(v)=\sum _{\alpha \beta \gamma }{S}_{k\gamma }^{j\beta }(v)S_{\gamma r}^{i\alpha }(u+v)S_{\beta q}^{\alpha p}(u)$$

これを先の統計重率の関係式と同一視することで、次の対応関係を得ます。

$$S_{jl}^{ik}(u)=w(i,j,k,l;u)$$

そして、統計重率(S行列)の条件として性質を満たすとします。これらは物理的な意味もある程度考えられますがしんどくなってきたので省略します。

初期条件

$$S_{jl}^{ik}(0)={\delta }_{il}{\delta }_{jk}$$

ユニタリー条件

$$\sum _{mp}{S}_{pl}^{mk}(u)S_{jm}^{ip}(-u)=\rho (u)\rho (-u){\delta }_{il}{\delta }_{jk}$$

第二ユニタリー条件

$$\sum _{mp}{S}_{pl}^{im}(\lambda -u)S_{mj}^{kp}(\lambda +u)\cdot {\left(\frac{r(m)r(p)}{r(i)r(j)r(k)r(l)}\right)}^{1/2}=\rho (u)\rho (-u){\delta }_{ij}{\delta }_{kl}$$

交差対称性

$$S_{jl}^{ik}(u)=S_{\overline{k}\overline{i}}^{jl}(\lambda -u)\cdot {\left(\frac{r(i)r(l)}{r(j)r(k)}\right)}^{1/2}$$

$$\overline{j}=-j,r(\overline{j})=r(j{)}^{-1}$$

電荷保存則

$$S_{jl}^{ik}(u)=0,(i+j\ne k+l)$$

パラメータ$\lambda$を交差パラメータ、$r(i)$を交差乗数と呼びます。

ここまでで準備は終わり。

そろそろ終わりたい

これまでに準備したものから、組みひも群の表現とMarkov traceを構成します。これさえ求めれば絡み目多項式ができるぞ！

演算子$X_i$を次のように定義します。最後の式は表記を省略しています。

$$\begin{array}{l}{X}_i(u)={\sum }_{abcd}{S}_{da}^{cb}(u)I^{(1)}\otimes \cdots \otimes I^{(i-1)}\otimes e_{ac}^{(i)}\otimes e_{bd}^{(i+1)}\otimes I^{(i+1)}\otimes \cdots \otimes I^{(n)}={\sum }_{abcd}{S}_{da}^{cb}(u)e_{ac}^{(i)}\otimes e_{bd}^{(i+1)}\end{array}$$

$$(e_{ab}{)}_{ij}={\delta }_{ai}{\delta }_{bj}$$

この演算子は次の関係式を満たします。

$$X_i(u)X_j(v)=X_j(v)X_i(u)(|i-j|\ge 2)$$

$$X_i(u)X_{i+1}(u+v)X_i(v)=X_{i+1}(v)X_i(u+v)X_{i+1}(u)$$

これは$u=u+v=v$となるとき組みひも群の定義式と一致します。

$$b_i{b}_j=b_j{b}_i\left(\left|i-j\right|\ge 2\right)$$

$$b_i{b}_{i+1}{b}_i=b_{i+1}{b}_i{b}_{i+1}$$

$u=v=0$とおくと自明な表現が得られるだけで全然うれしくないので$u=v=\infty$とします。こうして組みひも群の表現が得られます。

Markov traceも次のようにして得られます。

$$\varphi (A)=\mathrm{T}\mathrm{r}(H^{(n)}A)/(H^{(n)})(A\in {\mathcal{B}}_n)$$

$$H^{(n)}=h^{(1)}\otimes h^{(2)}\otimes \cdots \otimes h^{(n)}$$

$$(h^{(i)}{)}_{pq}=r^2(p){\delta }_{pq}$$

Markov traceが存在する十分条件は次のようになります。

$$\sum _l{S}_{lk}^{kl}(u)r^2(l)=H(u;\lambda )\rho (u)$$

$H$は特性関数と呼びます。長々と書きましたが、これでようやく絡み目多項式が導かれます。ちょっと統計力学と結び目のかんけいについて書きたかっただけなのになんでこんなことになったんだ...

結局

今考えている6頂点模型はスピン1/2の系になり、その場合の統計重率をもとめて絡み目多項式を作ると有名なJones多項式が得られます。

$$\alpha (A)={\left[t^{-1/2}(1+t)\right]}^{n-1}{\left[t^{1/2}\right]}^{e(A)}\varphi (A)$$

そこまで行きたかったのですが予想以上に長くなってしまったこととそろそろ疲れちゃったことから終わりにしたいと思います。こんな回りくどいことをやって絡み目の不変量を導くなんてすごいなぁと思いました(小並感)。

まとめ：

○絡み目不変量は可解格子模型から構成できる

○導出の過程でS行列とか使っててキモい

○6頂点模型からJones多項式が導かれる

特に山もオチもない記事で正直かなり失敗したなぁと思います。今回ぼくが学んだのは、人間ノリと勢いだけで生きていると燃料が切れた時に大変つらいなぁということです。僕のようにこんなことを毎回繰り返している人はもう手遅れな感じですが、みなさん計画的にスケジュール管理していきましょう。

明日の記事はxxkiritoxxさんとRondaiさんが担当です。