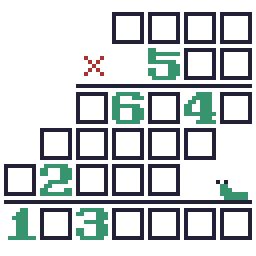2017/12/14 追記:練習問題(3)に別解がありました… 申し訳ありませんm(__)m
youjo_tapeさん報告ありがとうございます。圧倒的謝謝。
こんにちは。アドベントカレンダー2017/11/21担当のtsukatomoです。今年も去年に引き続きパズルを題材とした記事を書いていこうと思います。
去年は文系色の強い「クロスワード・パズル」について触れましたが、今年は理系大学生らしく「算数」を使ったパズルを紹介します。どちらも計算が必要となりますが、整数の加減乗除しか扱わないので、算数または数学が苦手という方もぜひ挑戦してみてください。
虫食い算
今回は算数パズルの王道「虫食い算」を紹介します。ご存知の方も多いとは思いますが、「虫食い算」は例えばこんな感じで出題されます:
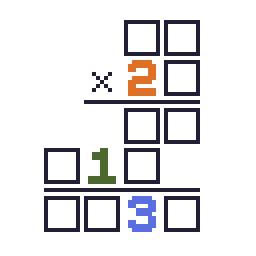
筆算の一部が□(虫食い)によって隠されています。これらの□を全て埋めて正しい筆算を復元することがこのパズルの目的です。ルールを細かく説明すると、
- それぞれの□に0~9の数字が1つずつ入る
- □の無いところに数字は入らない
- 最上位(各行の左端)の□に0は入らない
- 完成した筆算は正しくなければならない
となります。以上のことを踏まえて早速例題を解いてみましょう。
(次の節には例題の解法が書かれているので、自力で解きたい人は読まないようにしてください。)
虫食い算の解き方
さて、この例題の場合はどこから考えていくべきでしょうか?

説明しやすいように各マスにアルファベットを振りました。まずはCを考えてみましょう。
筆算より AB×C=DE となりますが、一方で AB×2=F1G です。ABとCの積が2桁なのに対し、ABと2の積は3桁になっていることが読み取れます。よってCは2より小さい数、すなわち1であることが確定します(C=0は筆算の形に合わないので不適切)。さらに AB×1=DE 、すなわち DE=AB であることも判明します。
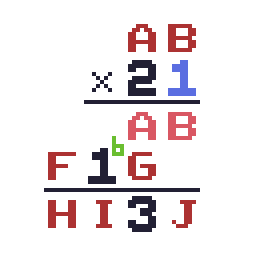
続いて AB×2=F1G に着目しましょう。 B×2 の十の位(筆算における繰り上がり)をbと置くと、 A×2+b=F1 と書くことができます。ここで A×2 は偶数、 F1 は奇数であるため、bは奇数となりますが、bが取り得る値は0か1しかないため、 b=1 が確定し、 B>=5 となります。
先ほどの式にb=1を代入すると A×2+1=F1 、つまり A×2=F0 が導けます。これを満たすAとFの組み合わせは A=5,F=1 しかあり得ません(∵F≠0)。
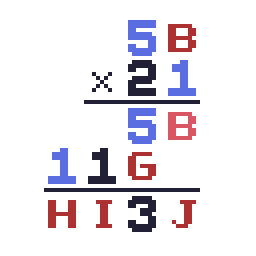
だいぶ盤面が埋まってきました。次は筆算の加算部分に注目します。
十の位より 5+G=13 であることが分かるので、 G=8 となります。よって B×2 の一の位が8となるので、 B>=5 より B=9 が確定します。
これにより乗数と被乗数が全て判明しました。あとは普通に筆算を解けば完成です!
解答
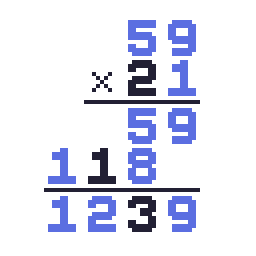
いかがでしたか?
この例題のように、虫食い算は
- 確定している数字を足がかりにして解いていく
- 桁数に注目する
- 繰り上がりに配慮する
ことが攻略のカギとなります。これらを常に念頭に置いて解いていきましょう。例題がスラスラ解けなかった人でも、何問か解いていくうちにコツが自然と身につくと思います。
練習問題
せっかくなので、問題をいくつか用意してみました。腕試しをしたい方はぜひ解いてみてください。
- 超初歩的な(クソ)問題。繰り上がりに注意。
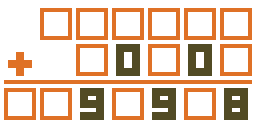
- まだ簡単な問題。2018年の年賀状にどうぞ

- 少し複雑です。2解あります。
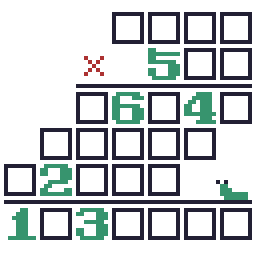
- 特殊な問題。 ● < 黒丸には8か3、□には8と3以外の数字が入るのかー。

- 虫食い算の応用、覆面算です。同じ文字は同じ数字、違う文字は違う数字に置き換わります。

ヒントと解答は次の節に載せておきました。どうしても解けない!という方は参考にしてください。
閲覧ありがとうございました!
明日は gomasio さんと ninja さんの記事です。お楽しみに!
ヒントと解答
練習問題のヒントと解答を載せておきます。
ヒント
1.全ての桁で繰り上がります。
2.一番下に注目。4桁-3桁=1桁ということは…?
3.□□□□×5=12□□□から、被乗数の千位が1通りに、百位が2通りに絞れます。さらに□□□□×□=□6□□□により、百位の数を1つに絞ることができます。
4.●が三つ並んでいる段に注目。3と8のみからなる3桁の数(8通り)を素因数分解してみましょう。
5.加算項と和の「じゅう」は相殺できます。「ごじゅう+000+はち+ろく+ろく=はち000」という式で考えてみましょう。違う文字が違う数字に置き換わることにも注意。
解答
- 999999+90909=1090908
- 662012/497=1332 あまり 8
- 2406×597=1436382 または 2407×597=1436979
- 419×725=303775
- 9846+846+10+72+72=10846