ビット演算で何が計算できるのか？

この記事は夏のブログリレー22日目の記事です

自己紹介

ブログを書くのは(個人では)初めてなので、簡単な自己紹介を。
　初めまして、@n3 (エヌさん)です。よく「エヌスリー」って読まれますが自称は「さん」です。ちなみに本名(?)は「n&(n//3)==0」です。高校からプログラミングを、大学から競技プログラミングを始めて、主にアルゴリズム班で活動しています。ちなみに名前の由来は後述します。

さて私は、高校一年生の時にとあるスライドを読んでからビット演算にハマってしまいました。ビット演算の魅力は、ビット演算を使うことで一部の計算に関してはif文などを使わずとも同様の計算ができて高速に動作するそしてその計算方法が技巧的であることです。
本ブログでは、そんな私がハマったビット演算の世界の片鱗を紹介したいと思います。

ビット演算とは

ビット演算には、論理演算であるAND, OR, NOT, XOR などと、シフト演算である右シフト, 左シフトなどがあります。(wikipediaにも同様の解説があります)
ビット演算について既に知っている人は、この節を読む必要はありません。

AND演算

ある2つの整数 $a, b$ のANDは、 $a & b$ と書いて、それぞれの整数を二進数展開して、その同じ桁ごとに論理積(両方が1のとき1、そうでない場合0)を取ったときの整数を返します。具体的には、
$a = 12, b = 6$ としたとき、

  a = 1100
  b = 0110
AND) ---------
      0100 = 4

のように、筆算の要領で各桁を計算することで、 $12&6 = 4$ と求めることができます。
Pythonやc++では、
a & b
と書くことで計算できます。

OR演算

ある2つの整数 $a, b$ のORは、 $a ∣ b$ と書いて、それぞれの整数を二進数展開して、その同じ桁ごとに論理和(少なくとも一方が1のとき1、そうでない場合0)を取ったときの整数を返します。具体的には、
$a = 12, b = 6$ としたとき、

  a = 1100
  b = 0110
OR ) ---------
      1110 = 14

のように、筆算の要領で各桁を計算することで、 $12∣6 = 14$ と求めることができます。
Pythonやc++では、
a | b
と書くことで計算できます。

NOT演算

ある整数 $a$ のNOTは、 $\neg a$ と書いて、その整数を二進数展開して、全ての桁において0と1を反転させた整数を返します。具体的には、
$a = 12$ としたとき、

  a = 1100
NOT) ---------
      0011 = 3

のように、筆算の要領で各桁を計算することで、 $\neg12 = 3$ と求めることができます(ただし数字は4bitであるとする)。
Pythonやc++では、
~a
と書くことで計算できます。

XOR演算

ある2つの整数 $a, b$ のXORは、 $a \oplus b$ あるいは $a ⊻ b$ と書いて、それぞれの整数を二進数展開して、その同じ桁ごとに排他的論理和(一方のみが1でもう一方は0のとき1、そうでない場合0)を取ったときの整数を返します。具体的には、
$a = 12, b = 6$ としたとき、

  a = 1100
  b = 0110
XOR) ---------
      1010 = 10

のように、筆算の要領で各桁を計算することで、 $12 \oplus 6 = 10$ と求めることができます。
Pythonやc++では、
a ^ b
と書くことで計算できます。Pythonで^がべき乗を表さないのは、慣習的に^が先に使われてたからでしょうか？

右シフト演算

ある整数 $a$ の右シフト<<kは(kは非負整数)、2進数においてその数の右に0をk個並べた数、つまり、 $2^{k}$ 倍された数を返します。具体的には、
$a = 12, k = 3$ としたとき、a<<k = $12 \times 2^{3} = 96$ を表します。
コードで書くと、12<<3 == 0b1100 << 3 == 0b1100000 == 96といった感じです。
Pythonやc++では、
a<<k
と書くことで計算できます。つまり $2^{k}$ を掛けるというのは、ビットをずらすだけの単純な命令になります。

左シフト演算

ある整数 $a$ の左シフト>>kは(kは非負整数)、2進数においてその数の右にk個の桁を無くした数、つまり、 $2^{k}$ で割った商を返します。具体的には、
$a = 12, k = 3$ としたとき、a>>k = $⌊ 12/ 2^{3} ⌋ = 1$ を表します。
コードで書くと、12>>3 == 0b1100 >> 3 == 0b1 == 1といった感じです。
Pythonやc++では、
a<<k
と書くことで計算できます。つまり $2^{k}$ で割った商を求めるのは、ビットをずらすだけの単純な命令になります。

ビット演算の公式

上で紹介した、AND, OR, NOT, XOR, 右シフト, 左シフトと四則演算を利用することで、様々な計算ができます。計算はどれもやや技巧的ですが、具体例をよく考えれば分かるのでゆっくり証明を読んでみてください。サンプルコードとしてPythonとc++を書いています。また、但し書きだ無い限りこの先nは非負であるとします。

「1になっている一番下の桁(LSB)」を求める

通称LSB：LeastSignificantBit とも言われます。n & -nとして求めることができ、たとえばn=11011100だったら、00000100を返します。nが0の場合は0を返します。
利用法として

その数が2で何回割れるかを求めれる
BIT(Binary Index Tree)^[1] の実装に使う

が上げられます。

コード

def LSB(n)
    return n & -n

int LSB(int n)
{
    return n & -n;
}

証明

具体例のほうが分かりやすいので、n=????1000という形を考える。ここで?は0か1のどちらでもよいとする。

  n = ????1000
 -n = ¿¿¿¿1000
  &) ---------
      00001000

まず、-nは(~n) + 1と表現できる^[2]。~n = ¿¿¿¿0111となるので(ここで?を反転させたbitを¿と表現した)、これに1を加えると¿¿¿¿1000になる。つまり、-nという操作によって

LSBより下位のbit → 0のまま変わらない
LSBより自身　　　 → 1のまま変わらない
LSBより上位のbit → 反転する

となることが分かった。よって、n&-nとするとLSBのみが残る。一般の場合も同様である。

「1になっている一番下の桁(LSB)」を0にする

先のLSBを取得する、と類似の方法で求めることができます。例えばn=11011100であれば、11011000を返します。先の結果を利用して、n - (n&-n)やn ^ (n&-n)と計算することもできますが、より簡潔にn&(n-1)と求めることもできます。n=0のときは0を返します。

コード

def offLSB(n):
    return n & (n-1)

int offLSB(int n)
{
    return n & (n - 1);
}

証明

具体的に、n=????1000という形を考える。

  n = ????1000
n-1 = ????0111
  &) ---------
      ????0000

まず、n-1 = ????0111となるので、この操作によって

LSBより下位のbit → 反転して1になる
LSBより自身　　　 → 反転して0になる
LSBより上位のbit → 変わらない

となることが分かった。よって、n&(n-1)とするとLSBが0になり、他は変わらない。一般の場合も同様である。

2の累乗か判定する

「nが2の累乗数である ⇔ 2進数で表現して立っている1が1個だけ」であるので、先のLSBを0にする、を利用することでn!=0 and n&(n-1)==0と表すことができます。

コード

def isPower2(n):
    return n != 0 and n & (n-1) == 0

int isPower2(int n)
{
    return n != 0 && (n & (n-1)) == 0;
}

証明

nが2の累乗数である ⇔ 2進数で表現して立っている1が1個だけ
であることに留意すると、n&(n-1)==0となるのは、n=0であるか、そうでないならば「LSBを0にすると全体が0になる ⇔ 二進数で1が1個だけの数 ⇔ 2の累乗数である」となるので、n != 0として例外的にn=0を除いてやることで、求める条件式を得る。

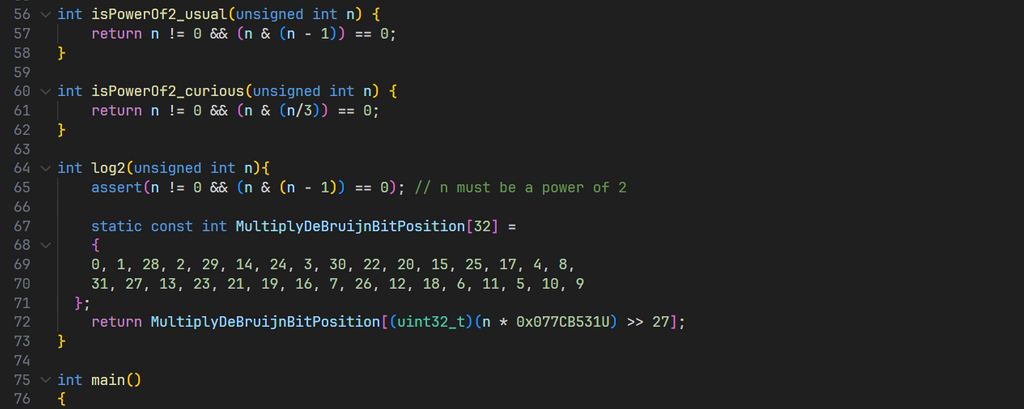
2の累乗か判定するVer2

実は、n&(n-1)==0という条件式とn&(n//3)==0という条件式は同値になります。そうですね私の本名はここから来ています。この式は自分が偶然^[3]発見した式で、ネットで調べても同じものが見つからなかったので、多分自分が発見者でいいと思います(既に発見されてたら:かなC++:)。

定理
$n & ⌊ \frac{n}{3} ⌋ = 0 ⟺ n = 0, 2^{k}$

コード

def isPower2(n):
    return n != 0 and n & (n//3) == 0

int isPower2(int n)
{
    return n != 0 && (n & (n/3)) == 0;
}

証明

n=3k,3k+1,3k+2の場合で場合分けをする。
また、 $k$ を二進数展開したときの表記を、k=...dcbaとすると(aは $2^{0}$ の位, bは $2^{1}$ の位, cは $2^{2}$ の位,...を表す)

n=3kのとき

$n & ⌊ \frac{n}{3} ⌋ = (3 k) & k$ となる。求める条件は、 $(3 k) & k = 0$ である。この計算を筆算のように計算を書くと、下のようになる。(a+bやc+dが繰り上がることは後で考える。なお一番上の行にある0は3kに加算さているものとする。)

                         0
  3k = ... c+d b+c a+b   a
   k = ...   d   c   b   a
 &)-------------------------
             0   0   0   0

ここで、 $2^{0}$ の位に着目すると、 $a & a = 0$ という等式が得られ、つまり $a = 0$ である。
次に、 $2^{1}$ の位に着目すると、 $a = 0$ より $a + b = b$ であるので、 $b & b = 0$ という等式が得られ、つまり $b = 0$ である。
次に、 $2^{2}$ の位に着目すると、 $b = 0$ より $b + c = c$ であるので、 $c & c = 0$ という等式が得られ、つまり $c = 0$ である。
...
以下同様にすることで、k=...00000 となる数であることが分かり、つまり $k = 0$ のみが求める答えである。

n=3k+1のとき

$n & ⌊ \frac{n}{3} ⌋ = (3 k + 1) & k$ となる。求める条件は、 $(3 k + 1) & k = 0$ である。この計算を筆算のように計算を書くと、下のようになる。(なお一番上の行にある1は3kに加算さているものとする。)

                         1
  3k = ... c+d b+c a+b   a
   k = ...   d   c   b   a
 &)-------------------------
             0   0   0   0

ここで、 $2^{0}$ の位に着目すると、 $((1 + a) mod 2) & a = 0$ という等式が得られる。これは $a = 0, 1$ のどちらでも成り立つ。

$a = 0$ のとき、繰り上がりは発生せず、上の筆算にa=0を代入すると以下のようになる。

                         1
  3k = ... c+d b+c   b   0
   k = ...   d   c   b   0
 &)-------------------------
             0   0   0   0

ここで $2^{1}$ の位以降を見ると、これはn=3kの場合に置いて、a→b, b→c, c→d とした状態と一致するので、自動的にb=c=d=...=0となる。よってk=0は解である...①。

$a = 1$ のとき、繰り上がりが発生することに留意して、上の筆算にa=0を代入すると以下のようになる。

                     1   1
  3k = ... c+d b+c 1+b   1
   k = ...   d   c   b   1
 &)-------------------------
             0   0   0   0

つまり、 $2^{1}$ の位に着目すると、 $((2 + b) mod 2) & b = 0 ⟺ b & b = 0$ であるので、 $b = 0$ である。これを更に代入すると、

                 1   1   1
  3k = ... c+d   c   1   1
   k = ...   d   c   1   1
 &)-------------------------
             0   0   0   0

ここで $2^{2}$ の位以降を見ると、n=3k+1のときにおいて、a→c, d→b, ... とした時の状態に一致する。よってこの議論より、kが $(3 k + 1) & k = 0$ の解であることと、kの右に01を追加したものが解になることは同値である。...②。

①より、2桁以内の数字の中で解になるのはk=0のみであり、これに②を繰り返し適用することで、k=0,001,00101,0010101,001010101, ...が求める解になることが分かる。つまりこの解は、 $k = \frac{2 ^{2 l} - 1}{3}$ と表せる( $l \in N_{\geq 0}$ )。このとき $n = 3 \cdot \frac{2 ^{2 l} - 1}{3} + 1 = 2^{2 l}$ となる。

n=3k+2のとき

$n & ⌊ \frac{n}{3} ⌋ = (3 k + 2) & k$ となる。求める条件は、 $(3 k + 2) & k = 0$ である。この計算を筆算のように計算を書くと、下のようになる。(なお一番上の行にある1は3kに加算さているものとする。)

                     1   0
  3k = ... c+d b+c a+b   a
   k = ...   d   c   b   a
 &)-------------------------
             0   0   0   0

ここで、 $2^{0}$ の位に着目すると、 $a & a = 0$ という等式が得られる。よって $a = 0$ である。これを代入すると、

                     1   0
  3k = ... c+d b+c   b   0
   k = ...   d   c   b   0
 &)-------------------------
             0   0   0   0

ここで $2^{1}$ の位以降を見ると、n=3k+1のときにおいて、a→b, b→c, ... とした時の状態に一致する。よって、kが $(3 k + 1) & k = 0$ の解であることと、kの右に0を追加したものが $(3 k + 2) & k = 0$ の解になることは同値である。...②。
よって、求めるkは、k=0,001,00101,0010101,001010101, ...の末尾に0を追加した、k=0,0010,001010,00101010,0010101010, ...が求める解である。つまりこの解は、 $k = \frac{2 ^{2 l + 1} - 2}{3}$ と表せる( $l \in N_{\geq 0}$ )。このとき $n = 3 \cdot \frac{2 ^{2 l + 1} - 2}{3} + 2 = 2^{2 l + 1}$ となる。

「n=3kのとき」「n=3k+1のとき」「n=3k+2のとき」をまとめる

以上の議論より、
n=3kのとき、 $n = 0$
n=3k+1のとき、 $n = 2^{2 l}$ 、つまり2の偶数乗
n=3k+2のとき、 $n = 2^{2 l + 1}$ 、つまり2の奇数乗
よって、これらより題意は示された。

「1になっている一番上の桁(MSB)」を求める

通称MSB：MostSignificantBit とも言われます。たとえばn=11011100だったら、10000000を返します。nが0の場合は0を返します。これまでの公式と違い、一本の式で書くことは難しいですが、右シフトとORを繰り返すことで $O (lo g lo g n)$ で求めることができます。
利用法としては、 $lo g_{2} (n)$ の整数部分を求める, などが挙げられます。

コード

def MSB(n):
    i = 1
    while n&(n+1):
        n |= n >> i
        i <<= 1
    return n ^ (n >> 1)

int MSB(int n)
{
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    return n ^ (n>>1);
}

証明

まずc++のコードを解説する。
具体的に、n=001?????という形を考える。

   n = 001?????
n>>1 = 0001????
   &) ---------
 n :=  0011????
 
   n = 0011????
n>>2 = 000011??
   &) ---------
 n :=  001111??
 
   n = 001111??
n>>4 = 00000011
   &) ---------
 n :=  00111111
 
(以下同様に繰り返す)...

   n = 00111111
n>>1 = 00011111
 　^ ) ---------
       00100000

まず、n |= n >> 1という操作によって、MSBからその1桁右までが1になる
次に、n |= n >> 2という操作によって、MSBからその3桁右までが1になる
次に、n |= n >> 4という操作によって、MSBからその7桁右までが1になる
...
というように、これらの操作を繰り返すことでMSBから右に十分な桁(c++のintは32bitなので、この操作を5回行えば十分)を1にすることができる。そこから1つ右シフトすることで、MSBのみが1になる。一般の場合も同様である。
Pythonコードに関しては、多倍長整数に対応するためにwhile文を用いています。n = 00111111のような1が連続している数は、つまりn+1が2の累乗数である、ということになるので、先の2の累乗か判定する、で述べた公式を使って終了を判定できます。

「1になっている一番下/上の桁(LSB/MSB)」を求める(二分探索で)

先に紹介した方法とは異なり、二分探索をすることでLSBやMSBはほぼ同様の手法で求めることができます。ただしMSBの上限が分かっていないと使えないためPythonで書くには不向きです^[4]。

コード

int LSB_BinarySearch(int n)
{
    n = n & 0x0000FFFF ? n & 0x0000FFFF : n;
    n = n & 0x00FF00FF ? n & 0x00FF00FF : n;
    n = n & 0x0F0F0F0F ? n & 0x0F0F0F0F : n;
    n = n & 0x33333333 ? n & 0x33333333 : n;
    n = n & 0x55555555 ? n & 0x55555555 : n;
    return n;
}

int MSB_BinarySearch(int n)
{
    n = n & 0xFFFF0000 ? n & 0xFFFF0000 : n;
    n = n & 0xFF00FF00 ? n & 0xFF00FF00 : n;
    n = n & 0xF0F0F0F0 ? n & 0xF0F0F0F0 : n;
    n = n & 0xCCCCCCCC ? n & 0xCCCCCCCC : n;
    n = n & 0xAAAAAAAA ? n & 0xAAAAAAAA : n;
    return n;
}

証明(雑)

MSB(最上位ビット)の場合
1行目では全体で32bitの中で上位16bitの中に立っているbitがあるかどうかを判定する
もしあるなら、最上位bitは上位16bitの中にあり、そうでないなら下位16bitにある
2行目では先の16bitの中で上位8bitの中に立っているbitがあるかどうかを判定する
もしあるなら、最上位bitは上位8bitの中にあり、そうでないなら下位8bitにある
...

これを繰り返すことで2分探索ができる。これはLSB(最下位ビット)の場合も同様である。

popcount(n) (立っているbitの個数を返す)

nを二進数で表したとき、その中で何個のbitが1になっているかを求める関数です^[5]。popcntと表記することもあります。例えば、n=010111010には1が6個あるので、popcount(01111010) = 6になります。「立っている数字を1の個数と見なす」というアイデアで、ビットマスクと加算を用いて実装できます。こいつもMSBの上限が分かってないと計算できないのでcppの場合のみ書きます。

コード

int popcnt(int n){
    n = n & 0x55555555 + ((n >> 1) & 0x55555555);
    n = (n & 0x33333333) + ((n >> 2) & 0x33333333);
    n = (n & 0x0F0F0F0F) + ((n >> 4) & 0x0F0F0F0F);
    n = (n & 0x00FF00FF) + ((n >> 8) & 0x00FF00FF);
    n = (n & 0x0000FFFF) + ((n >> 16) & 0x0000FFFF);
    return n;
}

証明

具体例で考える。n=11010010で考えたとき、これを

n = 1個 1個 0個 1個 0個 0個 1個 0個

と解釈してみる。この「〇個」を合計することを考えたい。
そこで、1行目のようにANDを取ると、

n & 01010101 = 01010000 =  　 1個  　 1個  　 0個  　 0個
n & 10101010 = 10000010 = 1個  　 0個  　 0個  　 1個

であるので、n & 10101010を右にシフトして

 n & 01010101       = 01 01 00 00 =  　 1個  　 1個  　 0個  　 0個
(n & 10101010) >> 1 = 01 00 00 01 =  　 1個  　 0個  　 0個  　 1個
+)----------------------------------------------------------------
                      10 01 00 01 =  　10個  　01個  　00個  　01個

とすることで、2桁区切りで見た時の塊に含まれる1の個数を求めることができる。同様に、

 n & 00110011       = 0001 0001 =  　  　  　01個  　  　  　01個
(n & 11001100) >> 2 = 0010 0000 =  　  　　  10個  　  　  　00個
+)----------------------------------------------------------------
                      0011 0001 =  　      0011個  　     0001個

とすることで、4桁区切りで見た時の塊に含まれる1の個数を求めることができる。

 n & 00001111       = 00000001 =  　  　  　  　  　  　  0001個
(n & 11110000) >> 4 = 00000011 =  　  　　    　  　  　  0011個
+)----------------------------------------------------------------
                      00000100 =  　          　  　     0100個

とすることで、8桁区切りで見た時の塊に含まれる1の個数を求めることができる。これが求めたかったものであるので、つまりpopcount(11010010)=4である。一般の場合も同様である。

DeBruijnSequenceで $2^{n}$ から $n$ を求める

DeBruijnSequenceとは、「ある文字数ごとにどこで区切っても、その文字数であり得る文字列すべてがちょうど一回ずつ現れる文字列」のことです。具体例としては、文字の集合として01, 切り取る文字数を5とした時のDeBruijnSequenceの一つは、
00000111011111001011010100110001
です。確かに、
00000111011111001011010100110001 → 0
00000111011111001011010100110001 → 1
00000111011111001011010100110001 → 3
00000111011111001011010100110001 → 7
00000111011111001011010100110001 → 14
...
00000111011111001011010100110001 → 24
00000111011111001011010100110001 → 17
00000111011111001011010100110001 → 2
00000111011111001011010100110001 → 4
00000111011111001011010100110001 → 8
00000111011111001011010100110001 → 16
のように太字の部分を二進数として見ると、同じ数字が現れないことが分かります(文字の最初と最後は繋がっているものだと見なします)。
この数字は16進数で0x077CB531になります。コードではこの表記を使っています。

この関数Npow2ToN(n)を利用することで、
Npow2ToN(MSB(n))で $lo g_{2} n$ の整数部分
Npow2ToN(LSB(n))で $n$ が何回 $2$ で割れるのか
などが分かります。

コード

int Npow2ToN(uint32_t n){
    // assert(n != 0 && (n & (n - 1)) == 0); // n must be a power of 2

    static const int MultiplyDeBruijnBitPosition[32] = 
    {
    0, 1, 28, 2, 29, 14, 24, 3, 30, 22, 20, 15, 25, 17, 4, 8, 
    31, 27, 13, 23, 21, 19, 16, 7, 26, 12, 18, 6, 11, 5, 10, 9
    };
    return MultiplyDeBruijnBitPosition[(uint32_t)(n * 0x077CB531U) >> 27];
}

証明

$n = 2^{k}$ とする。
このとき、n * 0x077CB531U = 0x077CB531U << kであるので、DeBruijnSequenceをk桁左にシフトすることを表す。これによって、DeBruijnSequenceのk-1文字目以前はオーバーフローによって無くなることになる。また、右シフトで(n * 0x077CB531U) >> 27として32bit中の下位27bitが無くなる。つまりDeBruijnSequenceのk+5文字以降はシフトによって無くなることを意味する。そうすると(n * 0x077CB531U) >> 27とは、DeBruijnSequenceのk~k+4文字目を2進数の数として返すコードである、と解釈することができる。これにより得られる数字は、32bitで表される2の累乗数と全単射の関係にあるので、前計算によって得られるテーブルを使うことでnを取得できる。

終わりに

ブログ書くのムズすぎだろ！
ネットで出てくる文章のツギハギの劣化版みたいな内容になってしまって申し訳ない:blob_sad:
実は、このブログはn&(n//3)==0を紹介したいがために書いたブログのため^[6]、構想段階からとてもネタが薄く...。人間はこうやってカスのブログを生産してしまうのか。

さて自分が知っているいい感じのビット演算の式はだいたい上で書いた通りなのですが、調べてみると他にも様々な技術が出てきます。popcnt(MSB(n))の計算をまとめて更に高速化したりとか、いろんなコードがあるようです。本当はそれぞれの関数の実行時間とかもまとめたかったんですが、今日になって急いで書いたせいで細かいことができませんでした:sad_eyes:

明日の投稿者は@vPhosさんです

過去に20Bの方がBITに関しての解説をしているっぽいです。このブログでもn&(-n)の解説がなされています ↩︎
-nは、nの2の補数である。よってビットを反転して+1するとも表現できる ↩︎
Pythonを使って、「ランダムな数式を延々と生成して、その式が『n=0か2の累乗数のときかつその時に限り0になる』という条件を満たすなら停止する」というプログラムを書いて、n&(n-1)==0の再発見をしようと思ったら、偶然この式が生成されて発見に至った ↩︎
まあ頑張ればPythonでもできます。負数とのANDを使って最上位ビット上限を求めれると思いますよ、面倒なのでやりたくないけど ↩︎
どうでもいいですが、 $n = 1 \sum \infty \frac{popcnt ( n )}{n ( n + 1 )} = ln 4$ という等式があります。美しいですね ↩︎
嘘です。このブログは次のブログの伏線にもなっているんですよね(回収するとは言ってない) ↩︎