こんにちは。理学院数学系2年のhatasa-yです。
traPでは最近までtiteQuestのプログラムを担当させていただいていまして完成となりました。
前回書いた記事は自分では完全にもの足りない結果と感じているので、また同じような内容で書こうと思います。
というわけで線形代数についてなるべく新入生にも分かるように書こうと思います。(ほんまか)
合同変換
合同変換の定義は、空間の点の変換で、二点間の距離を変えないもののことです。(ここでは、空間はユークリッド平面またはユークリッド空間のことを指します)
下の図のようにPQをP’Q’と変換させるのは合同変換となります。
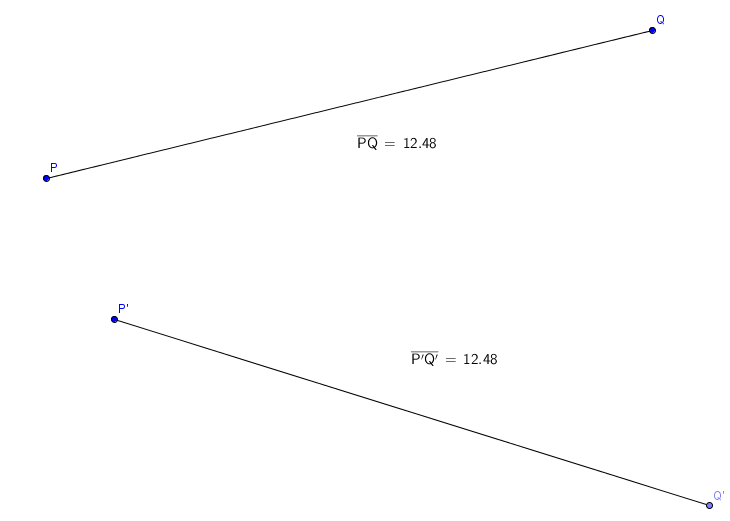
これより先は空間座標について考えますが、まず線形変換の定義について説明します。
線形変換
線形写像
定義
K上の線型空間VからK 上の線型空間V'への写像 が次の二条件を満たすとき、 をVからV'への線型写像と言う。
線形変換
定義
VからV自身への線型写像をVの線型変換と言う。
補足
K上の線型空間Vが何のことか分からない場合は線形代数の教科書を見てください。
今回議論しようとしている と は 上の線型空間です。
写像 が線形写像であれば、写像 は線形変換となります。
空間の合同変換
まず空間について原点OがO自身に移るような合同変換 について考えます。 が線形変換であることを示します。
まず3点O,P,Qが一直線上にあり、2点P,Qを合同変換させて点P',Q'に移ったときについて考えます。
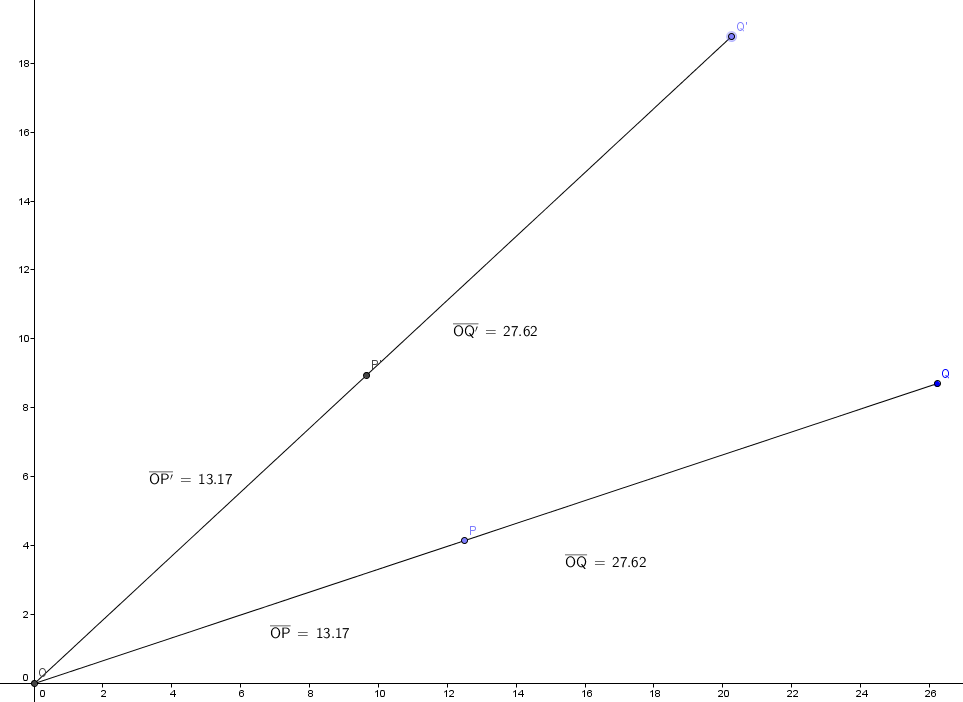 とおくと であります。
とおくと であります。
OQ=OP+PQであり原点OはO自身に移ることでOQ'=OP'+P'Q'が成り立つので、
O,P',Q'が一直線上にあることを示しています。
よって より
であるので が成り立ちます。
次に4点O,P,Q,Rが を満たすものについて考えます。
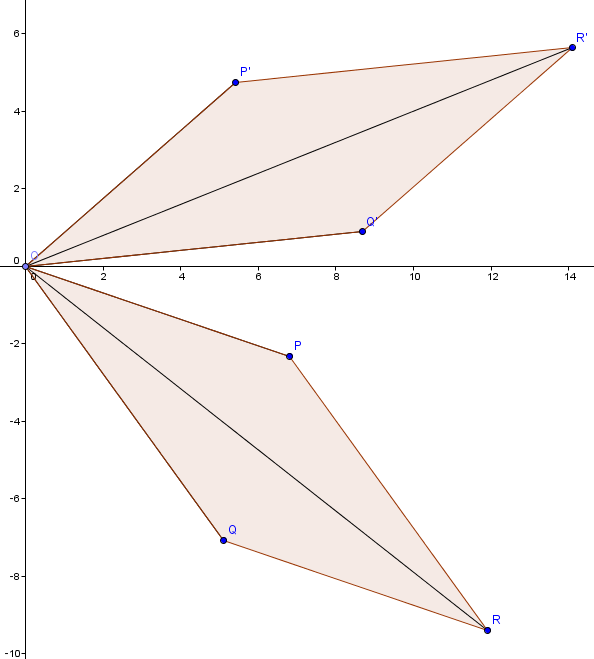 とおくと 三辺の長さを考えると、三角形は合同な三角形に移るので
とおくと 三辺の長さを考えると、三角形は合同な三角形に移るので
よって が成り立ちます。
これより合同変換 は線形変換となります。
また任意のxに対して が成り立ちます。
線形写像と行列表示
次の命題が成立する。(証明はしない)
命題
写像 に対し、次の同値関係が成立する。 が線形写像
補足
は存在して唯一という意味で、 はm×n型の行列です。
私が言いたいこと
これより先ほどの は線形変換(写像)であったので3×3型の行列 を用いて と表すことができる。
また が成立する。
直交行列
定義
n×n実行列 が、 を満たすとき、 を直交行列という。
次の命題が成り立つ。(証明はしない)
命題
n×n実行列 について次は同値である。
- (定義)
- の列ベクトル が の実標準内積に関して正規直交基底
- の行ベクトルの転置 が の実標準内積に関して正規直交基底
- 線形写像 は実標準内積について
- 線形写像 は実標準内積について
私が言いたいこと
が成立するので、上の7番が成立することになる。
これより行列 は直交行列となる。
空間の合同変換(続き)
平行移動
さて今までは原点OがO自身に移るような合同変換 について考えてきました。
まず初めに平行移動 を考えてみます。
原点OがO'に移るとして とおくと が成り立つ。
一般の合同変換
合同変換 について考えます。
原点OがO'に移るとして とおく。 とおくと、これは平行移動 の逆変換となる。 とおくと は合同変換であり、原点OをO自身に移すので となり となります。
非斉次位置ベクトル
ここで次のベクトル 及び行列 を考える。( を非斉次ベクトルと言う)
このとき
定理
以上のことをまとめると次の定理が言える。
空間の合同変換は、点の非斉次位置ベクトル の変換と考えることができ、それは、 に次の行列 を左からかけることによって得られる。 ただし は三次(平面の場合:二次)直交行列で は原点OがO'へと移る位置ベクトルである。
運動
合同変換 が、図形を裏返しにしないとき、 を運動という。
次の定理が成り立つ。(証明及び詳しい説明はしないことにする)
定理
合同変換 が運動であるのは、 が回転である場合である。 が回転であるためには、行列 の行列式が1であることが必要十分条件である。
補足
の行列式は の行列式は
平面の運動
2×2行列 が直交行列でかつ行列式が1となるものは を用いて として表すことができるので(証明は練習問題とする) となる。
幾何学的に関しては高校の数学でやったと思うのでここでは説明は省きます。
空間の運動
オイラー角
3×3行列で が直交行列でかつ行列式が1となるものは を用いて となります。
(証明には直交行列の固有値・固有ベクトル及び対角化の知識を持ってることが望ましい)
この をオイラー角といいます。幾何学的には下の図のようになります。
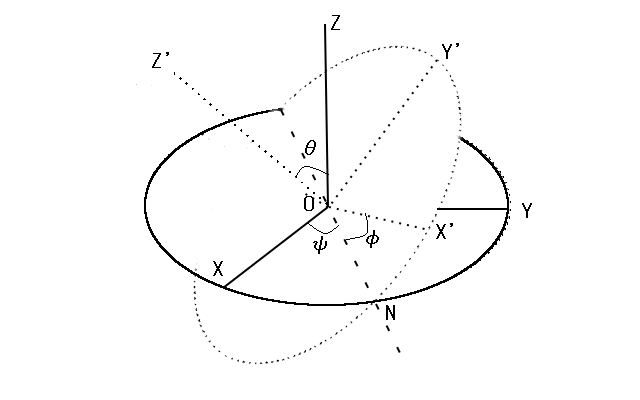
変換前の座標軸をX,Y,Zとし、変換後の座標軸をX',Y',Z'とすると はZ軸とZ'軸とのなす角になり、 はZ軸,Z'軸を含む平面とX軸,Y軸を含む平面との交線ONがX軸とのなす角になります。また はONがX'とのなす角になります。
ここでx軸のまわりの角 の回転を とし、z軸のまわりの角 の回転をそれぞれ とすると、 であり(参考:平面の運動) となります。(右辺を計算すれば上の式と一致します)
これより となります。
以上より平面の運動および、空間の運動について行列で表すことが出来ました。パチパチ
しかし
空間の運動の行列表示難しくないですか?
私はこれを理解するのにかなり時間がかかりました。(私が馬鹿なだけですごめんなさい)
オイラー角は歳差運動を扱うには便利なものです。しかしそれ以外の回転だと難しくて(できないわけではない)、実際にプログラムでもめんどくさいです。その理由にはいくつかあって
- オイラー角の視覚化が難しい
- 思うような回転をするのに計算がいる
- 3つ行列の積の計算が大変
- の計算が可換ではない
という訳で、プログラムではあんまり使いません。これよりも便利な回転があってプログラムではよくこちらの方を使います。
ロドリゲスの公式
オイラー角では3つの角を使って回転させるのに対して、ロドリゲスの公式は軸と軸のまわりの角度を使って回転をさせます。(ここは前回も書いたので同じような説明となります)
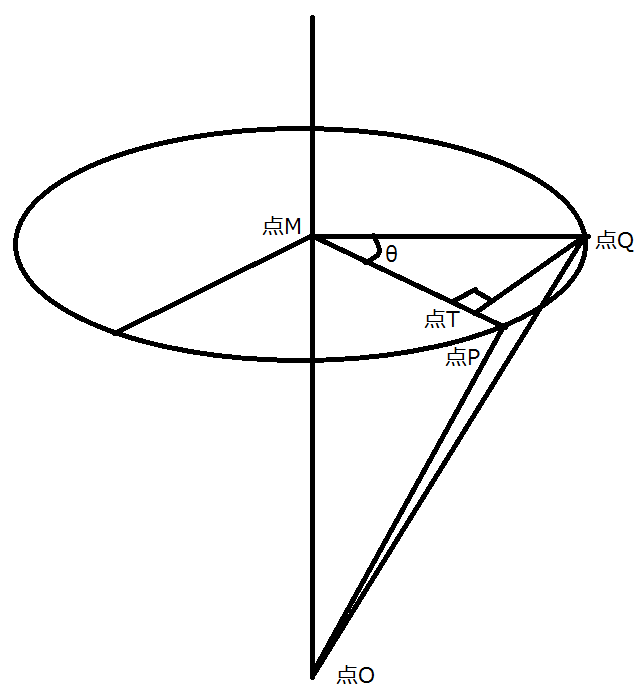
このような図を考えます。
ベクトル を回転軸ベクトル (ただし )の回りに角 回転させたベクトルを とし、 とします。 であるので となり (ただし )としてこれを計算すると、次のようになります。 これより行列 を使えば任意軸回転をすることができます。
これはオイラー角よりも視覚化が回転で行列計算も(簡単ではないけど)難しい訳ではなくなりました。
応用
理論ばかりだとつまらないのでロドリゲスの公式の応用として、@sobaya007のshaderの作品を紹介しようと思います。(画像をクリックしてください)
見れば分かるように「ホモ」が回転しているわけですがプログラムの一部を紹介しようと思います。
vec3 eye = vec3(0, 0, 500.);
vec3 xvec = vec3(1., 0, 0);
vec3 yvec = vec3(0, 1., 0);
vec3 n = normalize(vec3(1., 1., 1.));
float angle = 1. * iGlobalTime;
float c = cos(angle);
float s = sin(angle);
mat4 matrix;
matrix[0][0] = n[0]*n[0]*(1.-c)+c;
matrix[0][1] = n[0]*n[1]*(1.-c)-n[2]*s;
matrix[0][2] = n[2]*n[0]*(1.-c)+n[1]*s;
matrix[1][0] = n[0]*n[1]*(1.-c)+n[2]*s;
matrix[1][1] = n[1]*n[1]*(1.-c)+c;
matrix[1][2] = n[1]*n[2]*(1.-c)-n[0]*s;
matrix[2][0] = n[2]*n[0]*(1.-c)-n[1]*s;
matrix[2][1] = n[1]*n[2]*(1.-c)+n[0]*s;
matrix[2][2] = n[2]*n[2]*(1.-c)+c;
eye = (matrix * vec4(eye, 1.)).xyz;
xvec = (matrix * vec4(xvec, 1.)).xyz;
yvec = (matrix * vec4(yvec, 1.)).xyz;
時間が進むとiGlobalTimeが増えてmatrixの成分が変化することで、3つの軸の向きが変化して回転するようになっています。(今回はShaderの説明ではなくこんなものが作れるよという紹介でした)
おわりに
合同変換から始まって線形写像や直交行列の話もしながら、運動について話を進めてきました。ここまで読んでいただきありがとうございました。
上の話では出てこなかったのですが、オイラー角やロドリゲスの公式以外にもロールピッチョー角による回転行列もあってz軸、y軸、x軸の順に周りに回転させる行列もあります。また行列ではなく四元数を用いて合同変換および運動を表現する方法もあります。(気になる方は調べてください)
明日は最終回で@to-hutohuの「入部おめでとうございます&これからも入部歓迎です」と@Hummingの「誰でもわかる!モンハンにおけるダメージ計算」です。お楽しみに~
参考文献
斎藤正彦.線形代数学入門.東京大学出版会,1966
ランダウ,リフシッツ.力学.東京図書株式会社,1974
