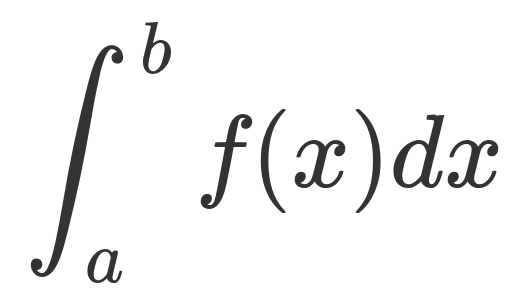こんにちは。アドベントカレンダー2017の11月2日担当のAzonです。この記事は積分についての高校生から大学学部一年生まで向けの読み物にしたいと思います。

高校数学における積分

高校数学において積分がどのように紹介されるかご存知ですか。まず微分の逆操作として不定積分が定義され、そこから定積分を定義します。そのあと、定積分が関数のグラフとx軸とのあいだの符号付き面積となることを証明したり、リーマン積分の片鱗を見せる区分求積法が紹介されたりします。しかし、積分はもともと微分と独立して定義できるものです。高校数学の定義では、原始関数が求まらない定積分を求めることが不可能になってしまいます。他にも問題があります。そもそも、面積とはなんでしょうか？　長方形や三角形などはともかく、任意の関数のグラフに対して面積が定義できるのでしょうか。この問題は測度論の発展とルベーグ積分の開発によって解決されましたが、筆者が詳しくない高校数学からいきなりそこまで話を広げるのは困難なので一旦置いておきます。

微分にも面積にも頼らない積分の定義

以上の問題を解決するために、微分にも面積にも頼らない積分の定義が欲しいですね。そこで区分求積法に目をつけます。区分求積法とは、

$$\underset{n\to \infty }{\lim }\frac{b-a}{n}\sum _{k=1}^{n}f(a+(b-a)\frac{k}{n})={\int }_a^{b}f(x)dx$$

という公式のことです。高校数学では、この公式を面積の存在を前提に証明しますが、逆に、この等式を定積分の定義とするのはどうでしょうか。つまり

$${\int }_a^{b}f(x)dx:=\underset{n\to \infty }{\lim }\frac{b-a}{n}\sum _{k=1}^{n}f(a+(b-a)\frac{k}{n})$$

とするのです。$:=$は左のものを右のもので定義するという意味です。この定義を定義1と呼ぶことにしましょう。定義1には微分も面積も関係ないので良さそうですね。しかし問題があります。$\mathbb{Q}$を有理数の集合とします。次のような関数$F$を考えてみましょう。

$$F(x)=\{\begin{array}{ll}1& (x\in \mathbb{Q})\\ 0& (x\notin \mathbb{Q})\end{array}$$

この関数$F$は原始関数が求まらないので、高校数学の定義では定積分が求まりません。しかし、定義1を使えば計算できそうですね。そこで定積分${\int }_0^{1}F(x)dx$、${\int }_1^{\sqrt{2}}F(x)dx$、${\int }_0^{\sqrt{2}}F(x)dx$を求めてみましょう。ヒントは、有理数$+$無理数$=$無理数、$0$でない有理数$\times$無理数$=$無理数であることです。できた人は分かると思いますが、

$${\int }_0^{1}F(x)dx+{\int }_1^{\sqrt{2}}F(x)dx={\int }_0^{\sqrt{2}}F(x)dx$$

が成り立ちません。定積分の性質を満たさないようでは、良い定積分の定義とは言えませんね。

リーマン積分

一度は失敗しましたが、諦めてはいけません。数学者ベルンハルト・リーマンは次のような定積分の定義を作りました。

定義

実数$a,b(a<b)$に対して、

$$a=x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b$$

を満たす数列を$\{x_k\}$とする。

$\{x_k\}$に対して、$L=\max \{x_k-x_{k-1}\mid k=1,2,\cdots ,n\}$とする。つまり、$x_1-x_0,x_2-x_1,\cdots ,x_n-x_{n-1}$のうち最も大きいものを$L$とする。

$\{x_k\}$に対して、$k=1,2,\cdots ,n$で

$$x_{k-1}\le t_k\le x_k$$

を満たす数列を$\{t_k\}$とする。

任意の関数$f$、$\{x_k\}$、$\{t_k\}$に対して、関数$S$を

$$S(f,\{x_k\},\{t_k\}):=\sum _{k=1}^{n}f(t_k)(x_k-x_{k-1})$$

と定める。

$L$がどんどん小さくなるように$\{x_k\}$を定めれば、どんな$\{x_k\}$、$\{t_k\}$に対しても$S(f,\{x_k\},\{t_k\})$がある一つの値に近づいていくならば、つまり

$$\underset{L\to 0}{\lim }S(f,\{x_k\},\{t_k\})=\underset{L\to 0}{\lim }\sum _{k=1}^{n}f(t_k)(x_k-x_{k-1})$$

が収束するならば、関数$f$はリーマン積分可能といい、この極限の値を${\int }_a^{b}f(x)dx$とする。

リーマン積分不可能な関数

このややこしい定義のおかげで、先ほどの関数$F$などはリーマン積分不可能ということになります。$L$を小さくしながらも$\{t_k\}$が常に有理数になるように$\{x_k\}$、$\{t_k\}$を定めれば、

$$\underset{L\to 0}{\lim }S(F,\{x_k\},\{t_k\})=b-a$$

ですが、逆に$L$を小さくしながらも$\{t_k\}$が常に無理数になるように$\{x_k\}$、$\{t_k\}$を定めれば、

$$\underset{L\to 0}{\lim }S(F,\{x_k\},\{t_k\})=0$$

となります。$\underset{L\to 0}{\lim }S(F,\{x_k\},\{t_k\})$が一つの値に近づいていないので関数$F$はリーマン積分不可能です。

区分求積法からリーマン積分へ

実は、$x_k=t_k=a+(b-a)\frac{k}{n}$とおけば、リーマン積分の定義は定義1と同じものになります。実際にやってみましょう。

$$\underset{L\to 0}{\lim }\sum _{k=1}^{n}f(t_k)(x_k-x_{k-1})=\underset{L\to 0}{\lim }\frac{b-a}{n}\sum _{k=1}^{n}f(a+(b-a)\frac{k}{n})$$

であることは$x_k=t_k=a+(b-a)\frac{k}{n}$を代入すればすぐ分かりますね。さらに、$x_1-x_0=x_2-x_1=\cdots =x_n-x_{n-1}=\frac{k}{n}$なので、$L=\frac{k}{n}$です。したがって、$L\to 0$ならば$n\to \infty$なので、

$$\underset{L\to 0}{\lim }\sum _{k=1}^{n}f(t_k)(x_k-x_{k-1})=\underset{n\to \infty }{\lim }\frac{b-a}{n}\sum _{k=1}^{n}f(a+(b-a)\frac{k}{n})$$

となるわけです。つまり、リーマン積分というのは定義1による積分を一般化したものなのです。

逆に、リーマン積分可能ならば、どのような$\{x_k\}$、$\{t_k\}$のとり方をしても$S(f,\{x_k\},\{t_k\})$は同じ値に収束するので、リーマン積分の値は定義1による積分の値と一致します。実は、連続関数はリーマン積分可能であることが証明できます。したがって、連続関数に対してなら定義1を使っても正しいリーマン積分の値を求められます。さらに、リーマン積分は高校数学で学んだ積分の性質を全て満たします。しかも、リーマン積分から不定積分を定義すれば微分の逆操作にもなります。それらの証明はめんどくさいここに書くにはサーバ容量が狭すぎるため、大学で学んでくれること（あるいは独学）を期待して読者への課題としたいと思います。リーマン積分についてもっと詳しく知りたいという方はダルブーの定理、微分積分学の基本定理などについて調べてみるといいと思います。

微分も面積も使わない、純粋な積分の定義というものを少しでも肌で感じていただけましたら幸いです。
アドベントカレンダー2017明日の担当はringさんとmaboさんです。ご期待ください。