こんにちは。traP Advent Calendar 2016 20日目担当のhatasa-yです。

traPでは現在titeQuestのプログラムを担当させていただいています。

いやークリスマスまであと5日ですよー！みなさん予定入ってますか？

僕は予定入ってますよー

数学&進捗

というわけで僕からは線型代数について話したいと思います。(題名と違うじゃないか!)

線型代数とはベクトル空間と線型写像を中心とした代数学の一分野であります。

簡単に言うと、ベクトル空間とは和とスカラー倍の2種類の演算(線型演算)が定義できている空間のことで、線型変換とは線型演算を保存するように、ベクトル空間からベクトル空間への対応のことをいいます。(詳しく知りたい人は線型代数の本を見てください)

理系学部の大学一年生では微分積分学と共に習っていると思います。理工系だけでなく社会科学系の学部でも線型代数の講義が行われていることもあるでしょう。

線型代数は幅広いところで応用されています。プログラムで座標を考える際はかなり線型変換が重要になってきます。ここでは座標の線型変換の一例として回転について紹介したいと思います。

２次元における回転

高校数学では行列 $\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$ の定める線型変換 $\left[\begin{array}{c}x\\ y\end{array}\right]\mapsto \left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$ が平面 ${\mathbb{R}}^2$ の原点を中心とした角 $\theta$ の回転であると習ったと思います。 $I=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],J=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$ とおくと $\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]=I\cos \theta +J\sin \theta$ であるが、 $J^2=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]=-I$ $I=1$ のようにして実数としてみると $J=i$ となります。

よって平面 ${\mathbb{R}}^2$ を複素数平面 $\mathbb{C}$ として考え、 $z=x+iy,z^{\prime }=x^{\prime }+i{y}^{\prime }$ とおくと $z\mapsto z^{\prime }=(\cos \theta +i\sin \theta )z$ 人によってはこちらを高校数学で習った方もいらっしゃると思います。

回転という概念を用いて角 $\theta$ 及び三角関数 $\cos \theta ,\sin \theta$ を定義することができますがここでは省略します。

３次元における回転

2次元における回転はできたので、3次元についてはどうだろうかと考える人は多いと思います。

実は3次元でもロドリゲスの公式と呼ばれる回転を表す線型変換はあります。 $\left[\begin{array}{ccc}\cos \theta +n_1^2(1-\cos \theta )& n_1{n}_2(1-\cos \theta )-n_3\sin \theta & n_1{n}_3(1-\cos \theta )+n_2\sin \theta \\ n_2{n}_1(1-\cos \theta )+n_3\sin \theta & \cos \theta +n_2^2(1-\cos \theta )& n_2{n}_3(1-\cos \theta )-n_1\sin \theta \\ n_3{n}_1(1-\cos \theta )-n_2\sin \theta & n_3{n}_2(1-\cos \theta )+n_1\sin \theta & \cos \theta +n_3^2(1-\cos \theta )\end{array}\right]$ ただし $\mathbf{n}=[n_1,n_2,n_3]$ は大きさ1の回転軸ベクトルである。

初めて見たときは流石になんだこれ！？って思いました。(今でもそうですが)

これについて説明する気はありません。なぜかというとめんどくさいからです。

というわけでこの記事は終了です。

というのはあまりにも酷すぎるのでなんでこんな式になるか軽く説明しておきましょう。

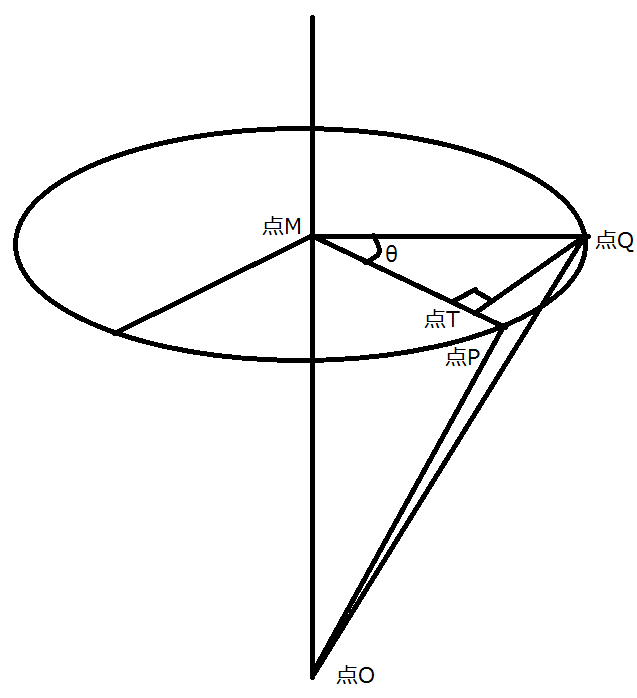
このような図を考えます。

ベクトル $\mathbf{r}$ を回転軸ベクトル $\mathbf{n}$ の回りに角 $\theta$ 回転させたベクトルを ${\mathbf{r}}^{\prime }$ とし、 $OP=\mathbf{r},OQ={\mathbf{r}}^{\prime }$ とします。

${\mathbf{r}}^{\prime }=OM+MT+TQ$ であるので ${\mathbf{r}}^{\prime }=\mathbf{n}(\mathbf{n},\mathbf{r})+(\mathbf{r}-\mathbf{n}(\mathbf{n},\mathbf{r}))\cos \theta -(\mathbf{r}\times \mathbf{n})\sin \theta$ となり ${\mathbf{r}}^{\prime }=\mathbf{r}\cos \theta +\mathbf{n}(\mathbf{n},\mathbf{r})(1-\cos \theta )-(\mathbf{r}\times \mathbf{n})\sin \theta$ ${\mathbf{r}}^{\prime }=[x^{\prime },y^{\prime },z^{\prime }]$ , $\mathbf{r}=[x,y,z]$ , $\mathbf{n}=[n_1,n_2,n_3]$ としてこれを計算すると、 $\mathbf{r}$ から ${\mathbf{r}}^{\prime }$ への変換は線形写像となり、上で述べたロドリゲスの公式となります。

3次元で回転を考える際には、必ず回転軸となるものが存在します。その軸と回転角度を設定することでどんな回転も表すことが出来ることが分かりました。実際にゲームを作るときはこの行列を使ってプログラムを書くことだと思います。

最後に

どうでしたか？読んでいても線型変換がよく分からないと思った方もいるかもしれませんが、行列を使って回転を表すことができ、プログラムにも活用できるという紹介でした。

明日はcrotkaz, naosan, parumaさんの3本となります。お楽しみに。