こんにちは。@shobon です。この記事は新歓ブログリレー2023 4日目の記事です。
記事の目的
この記事では、競プロ(競技プログラミング)の裏技的存在であるOEISエスパーについて解説していきます。OEISエスパーとは、「オンライン整数列大辞典」(OEIS) を活用することで問題の本質的な考察をスキップして正解することを言います。
記事の対象は ABC(AtCoder Beginner Contest) で2問以上解ける実力を持つ人・計算量を知っている人です。計算量を知らない人は次の記事をご覧ください。
計算量オーダーの求め方を総整理! 〜 どこから log が出て来るか 〜 - Qiita (drken さん)
また、記事内で ABC172-D, ARC144-D, CF 1726E (Round 819) のネタバレを含みますのでご了承ください。
OEISとは?
OEIS とはどのようなサイトでしょうか?OEIS は無料で使える整数列のデータベースです。掲載されている数列は約 個(2023年3月現在)もあり、競プロや数学で謎の数列が出現したときに OEIS に入れると引っかかることも多いです。
たとえば から までの総和を並べた数列(三角数) は A000217 に相当します。OEIS にはただ数列が載っているだけではなく、その数列に関する情報がたくさん載っています。
競プロで数列を扱うことは多いので、しばしば OEIS に載っている情報を活用して問題に正解するコードを書くことができます。特に定数個入力( だけが与えられるなど)の確率・数え上げ・総和の問題では OEIS エスパーがよく効きます。それでは、OEIS エスパーの具体例を見ていきます。
問題
問題文
正整数 に対して、 を の正の約数の総和と定めます。正整数 が与えられるので、
を で割った余りで求めてください。
制約
- 時間制限 秒 / メモリ制限 MB
OEISエスパーで解いてみよう!
問題を見てみるとかなり難しそうです。実際に AtCoder Beginner Contest などでこの問題が出たらF問題あたりに配置されるような難易度になっています。
しかし、OEIS を活用すると、この問題は驚くほど簡単に解けてしまいます。
まずは愚直なコードで が小さいときの値を求めてみましょう。本当に愚直でよいです。(OEISエスパーでなくても、愚直なコードを書いて高速化したコードと値を比較すること自体はよくやります)
def naive(n):
ans = 0
for i in range(1, n+1):
tmp = 0
for j in range(1, i+1):
if i % j == 0:
tmp += j
ans += i * tmp
return ans
for i in range(1, 10):
print(i, naive(i))
実行結果は次のようになります。
1 1
2 7
3 19
4 47
5 77
6 149
7 205
8 325
9 442
OEIS で 7, 19, 47, 77, 149, 205 を検索してみると、(第1項は省略されたり異なる場合があるので、第2項・第3項から検索した方がよいです)
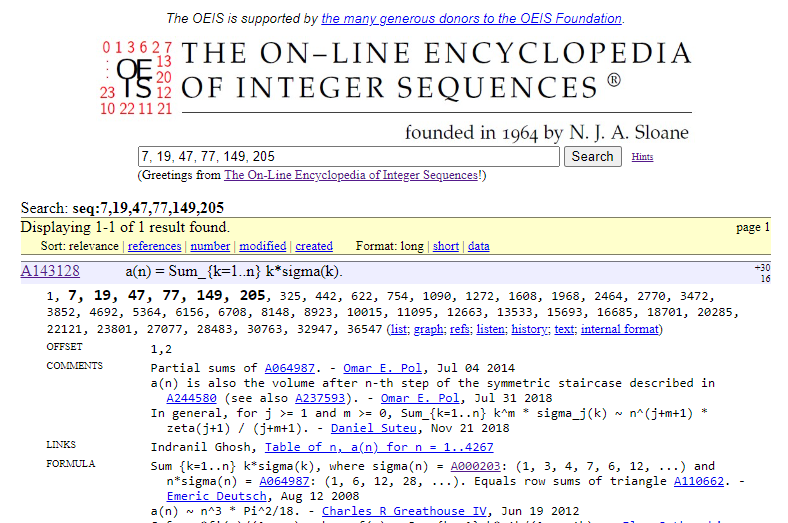
A143128 が引っかかりました。「FORMULA」という欄に注目しましょう。 として、 に関する様々な式が書いてあります。 という制約に間に合いそうなもの( など)を探してみましょう。じっと睨むと、

a(n) = Sum_{k=1..s} (k*A000330(floor(n/k)) + k^2*A000217(floor(n/k))) - A000330(s)*A000217(s), where s = floor(sqrt(n)). - Daniel Suteu, Nov 26 2020
と書いてあります。A000330 は の和 、A000217 は の和 を表しているので、結局
としたとき、
となります。他にも、「PROG」の欄には
(PARI) f(n) = n*(n+1)*(2*n+1)/6; \\ A000330
g(n) = n*(n+1)/2; \\ A000217
a(n) = sum(k=1, sqrtint(n), k * f(n\k) + k^2 * g(n\k)) - f(sqrtint(n)) * g(sqrtint(n)); \\ Daniel Suteu, Nov 26 2020
と、上の式と同じことが書いてあります。これを実装すると、
mod = 998244353
inv2 = pow(2, mod-2, mod)
inv6 = pow(6, mod-2, mod)
def f(n):
n %= mod
return n * (n+1) % mod * (2*n+1) % mod * inv6 % mod
def g(n):
n %= mod
return n * (n+1) % mod * inv2 % mod
def floorsqrt(n):
# only for n <= 10 ** 18
ok = 10 ** 9 + 10
ng = 0
while ok - ng > 1:
t = (ok + ng) // 2
if t * t > n: ok = t
else: ng = t
return ng
def solve(n):
s = floorsqrt(n)
ans = - f(s) * g(s) % mod
for i in range(1, s + 1):
ans += (i * f(n // i) + i * i % mod * g(n // i)) % mod
ans %= mod
return ans
n = int(input())
print(solve(n))
このようになります(今回の場合、floorsqrt(n) は int(n ** .5) でも構いませんが、 が よりも大きくなってしまうと誤差が発生する場合があるので注意してください)
計算量は なので間に合いそうです。これを提出すれば AC が得られます! おめでとうございます!!!!!
え?
やったことといえば、
- 小さいケースを計算する
- OEISで数列を検索する
- 間に合いそうな公式を見つける
- 頑張って実装する
です。なんと「問題自体を考察する」という要素が1回も出てきていません。愚直コードを実装し、出てきた式から高速なコードを実装するとAC出来ます。このように、OEISでエスパーすると問題の本質的な部分を無視することができます。
また、この問題は ABC172 D - Sum of Divisors のパクリです。ABC172 D でもOEISエスパーが使えますので、練習したい人はいいかもしれません。
おまけ:実際にはどうやるのか?
(記事の本筋から外れるので飛ばしていいです)
とします。
主客転倒
主客転倒というテクニックを使います。 ごとにみるのではなく、正整数 が約数としてどのくらい出現しているかを見ます。
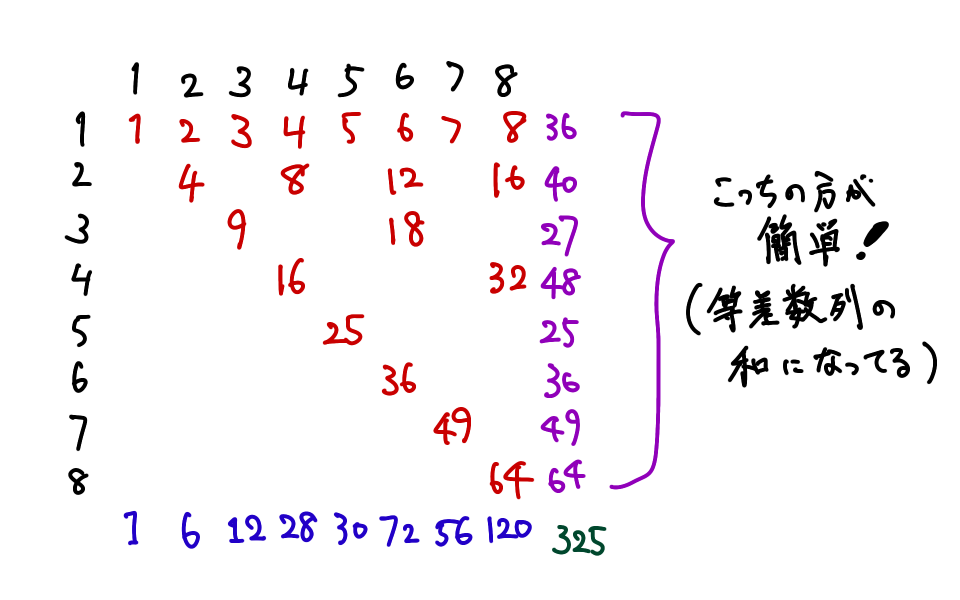
正整数 であって、 が の約数であるようなものの の総和を とします。たとえば のとき、 は の約数、 の約数、 の約数として現れるので です。そうすると、
が導きます。 は 以上 以下の の倍数の総和なので、等差数列の和より
よって
が導きます。この時点で が出来ました!しかし今回は あたりが要求されているので、ここからさらに高速化します。
高速化
に対し、 がとりうる値はだいたい 個であることが知られています。これに注目してもう一回主客転倒を行います。
を固定し、 となる についての の総和を とします。このとき
が従います。平方分割などを使ってありうる を列挙し、 となる の範囲を調べれば、 が導いて、結局 で解くことができます!
楽な の列挙方法は次の記事に書きました(宣伝)
連載 しょぼんコーダー 5 floor(N/i)を楽に列挙する方法 - しょぼんブログ
コードは以下のようになります。
mod = 998244353
inv2 = pow(2, mod-2, mod)
inv6 = pow(6, mod-2, mod)
def sum2(x):
x %= mod
return x * (x + 1) % mod * (2 * x + 1) % mod * inv6 % mod
def solve(n):
ans = 0
i = n
while i > 0:
v = n // i
j = n // (v + 1)
v %= mod
ans += v * (v + 1) % mod * (sum2(i) - sum2(j)) * inv2 % mod
i = j
ans %= mod
return ans
n = int(input())
print(solve(n))
OEISエスパーの問題点
次を求める問題だったらどうだったでしょうか。
この場合、OEISに数列は載っていません。しかし、ちゃんと考察したら の場合とほぼ労力は変わらず解けてしまいます。
OEISエスパーは考察をスキップできる反面、非教育的です。問題ごとにその場限りの解法を書くので、一般的なテクニックが何も身につかないおそれがあります。レートを賭けたコンテスト中はいいですが、ちゃんと復習するようにしましょう。
ただし、本質的な部分は分かっていて時間短縮に使うとき( の一般項、ゲームの grundy数など)を知る分にはいいと思います。
問題 (ARC144-D のネタバレを含みます)
AtCoder Regular Contest 144 の D 問題を見ます。
https://atcoder.jp/contests/arc144/tasks/arc144_d
Difficulty は 2468 となっており、かなり難しめの問題です。問題文は該当ページをご確認ください。
愚直解
まずは愚直解を書いてみます。python 使いの方は itertools が愚直コード生成に便利です。
import itertools
def naive(n, k):
ans = 0
for f in itertools.product(range(k+1), repeat=1<<n):
mode = 1
for x in range(1<<n):
for y in range(1<<n):
if f[x]+f[y] != f[x&y]+f[x|y]:
mode = 0
break
if mode == 0: break
if mode: ans += 1
return ans
OEISで見つける
今回与えられる入力は の 個です。そのうち 個を固定した数列を考えます。とくに今回は の小ささに対し と非常に大きくなるので、まずは を固定してみます。 の場合の答えを とします。
に固定すると
に固定すると
に固定すると
と出てきます。 は OEIS を使わなくても とエスパーできますね。しかし の場合はパッと見では分かりません。そこで、OEISに入れてみます。
すると、 の場合は A005900 が、 の場合は A014820 が引っかかりました。すなわち、
がエスパーできます。睨むだけでも、 を固定すると に関する 次多項式になりそうですね!
法則性の発見へ・人力エスパー
は愚直では厳しそうです。 の 「FORMULA」 を観察してみます。
a(n) = binomial(n+2,3) + 2*binomial(n+1,3) + binomial(n,3), (this pair generalizes; see A014820, the 4-cross polytope numbers).
a(n-1) = C(n+3,4) + 3 C(n+2,4) + 3 C(n+1,4) + C(n,4).
に限っては の場合の数列である「A014820」へのリンクも丁寧に載っています。じっと睨むと、二項係数の和の「係数」がふたたび二項係数になっていることに気付きます。すなわち、
が見えます。これを一般化しようとすると、次の疑惑がうまれます。ここは人力でエスパーします。
これは正しいのでしょうか? の場合に計算すると、 となるので正しいです。さらに、 であり、これも正しいです。よって、エスパーに成功したと思っていいでしょう。こうして、実装に移ることができます。
実装
あとは丁寧に実装するだけです。 なので まわりの処理を気をつける必要があります。実装はそこそこ複雑なので省きます。
問題 (CF819 (Div.1+2) - E のネタバレを含みます)
Codeforces Round 819 (Div. 1 + Div. 2) and Grimoire of Code Annual Contest 2022 の E 問題を見ます。
https://codeforces.com/contest/1726/problem/E
この問題の難易度は 2400 で、AtCoder では黄Diff上位相当といったところです。問題文は英語で書かれていますので、日本語に訳します。
問題文
長さ の順列 がほぼ完全とは、すべての整数 に対して を満たすことを言うこととします。ただし、 とは、 の逆順列(すなわち と が同値である)とします。
テストケースについて、 が与えられるので、長さ のほぼ完全な順列の個数を で割った余りで求めてください。ただし、テストケース全体で の総和は を超えません。
愚直解
もう慣れっこですかね? 順列は itertools.permutations を使えば簡単に全列挙できるので便利です。
import itertools
def naive(n):
ans = 0
for p in itertools.permutations(range(n)):
q = [0] * n # 逆順列
for i in range(n):
q[p[i]] = i
mode = 1
for i in range(n):
if abs(q[i] - p[i]) > 1:
mode = 0
break
if mode:
ans += 1
return ans
目的の数列を とします。 は と続きます。
いつものようにOEISに…ない!?
OEISで 1, 2, 4, 12, 32, 100, 312, 1076, 3772 を調べると… なんとありません!!
第2項・第3項以降だけを検索するテクニック
数列によっては「第1項は例外で、第2項以降だけがOEISに載っている」ということがしばしばあります。これは、定義によって第1項だけ異なったり省かれたりするが、第2項以降は同じということがあるからです。よって、「第1項を外して第2項・第3項以降だけを検索する」ということを考えます。
OEISで 4, 12, 32, 100, 312, 1076, 3772 を調べると… なんとありません!!(すべて で割るとそれっぽいのは出ますが違います)
残念ながら今回は第2・第3項以降だけを検索するテクニックは使えなかったみたいです。
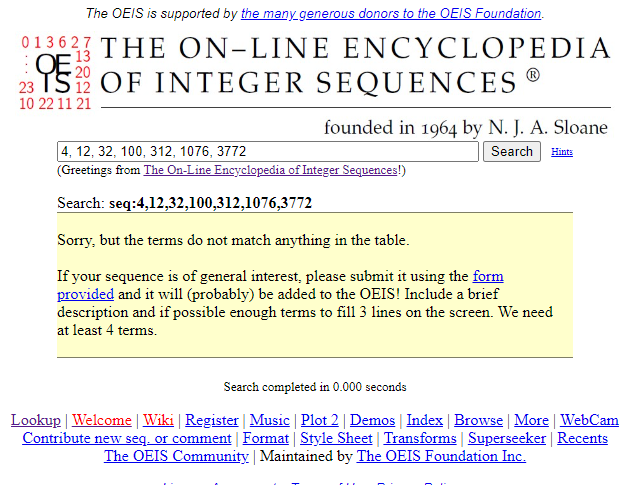
あえて分解するテクニック
果たしてどうすればよいのでしょうか?ここで活躍するのが「あえて分解するテクニック」です。 を計算する上で数えるべき対象をまとめずに、あえて 個に分解したものを数え上げてみましょう。
を満たす順列 をを特徴的な量で分類します。もちろん、 のうち になる個数で場合分けしますよね!(実際はいろいろ試します)というわけで、分類してコードを書いてみます。
import itertools
def naive(n):
ans = [0] * (n+1)
for p in itertools.permutations(range(n)):
q = [0] * n # 逆順列
for i in range(n):
q[p[i]] = i
mode = 1
cnt = 0
for i in range(n):
if abs(q[i] - p[i]) > 1:
mode = 0
break
if abs(q[i] - p[i]) == 0:
cnt += 1
if mode:
ans[cnt] += 1
return ans
for i in range(1, 13):
print(i, naive(i))
実行結果は以下のようになります。
1 [0, 1]
2 [0, 0, 2]
3 [0, 0, 0, 4]
4 [2, 0, 0, 0, 10]
5 [0, 6, 0, 0, 0, 26]
6 [0, 0, 24, 0, 0, 0, 76]
7 [0, 0, 0, 80, 0, 0, 0, 232]
8 [12, 0, 0, 0, 300, 0, 0, 0, 764]
9 [0, 60, 0, 0, 0, 1092, 0, 0, 0, 2620]
10 [0, 0, 360, 0, 0, 0, 4256, 0, 0, 0, 9496]
11 [0, 0, 0, 1680, 0, 0, 0, 16704, 0, 0, 0, 35696]
12 [120, 0, 0, 0, 8400, 0, 0, 0, 68760, 0, 0, 0, 140152]
美しい感じになりました。横方向に注目すると、 つごとに でない値が現れてますね!今回は斜めに現れている数列を見てみます。
まずは一番右端、 を探すと、A000085 が現れます。「FORMULA」を見ると、D-finite with recurrence a(0) = a(1) = 1, a(n) = a(n-1) + (n-1)*a(n-2) for n>1.
ということで、 で計算できそうです。
なにかの値で加減乗除するテクニック
さて、二番目、 の正体を暴きます。OEISで調べると… なんとありません!!
ここで「なにかの値で加減乗除するテクニック」を使います。その値が直接OEISになくても、その値から階乗や などで割ったり、定数を足し引きしたりすると OEIS に出現する場合があります。今回, すべてを で割って で調べると、A162970 が引っかかります!
「FORMULA」を見ると、a(n) = (1/2)*n*(n-1)*I(n-2) for n>=2, where I(n)=A000085(n) is the number of involutions of {1,2,...,n}. ということで、さきほど出てきた A000085 と関連が出てきます。
最後は人力エスパー
それでは三番目、 の正体を暴きます。OEISで調べると… もちろんありません!! すべてを で割って を検索すると、…出てきません!すべてを で割って を検索すると、…出てきません!
これはピンチです。この場合、問題2でやったように人力でエスパーすることが必要です。一段目を として、二段目は ということが分かっています。ということは、三段目は のようになることが予想できますね!
実際に計算してみると、 が出てきます。これは三段目の 倍の値になっています。よって三段目は であることがエスパーできました。
四段目はもはや時間の問題で、同様に であることがエスパーできます。一番最初は であることがわかっているので、 を解いて です。
ということは、階乗の逆数が知りたい係数になっている可能性が高そうです。 段目の最初が から始まっているのを見て、求める式は
とエスパーできます。数列 は で まで列挙できるのでOKです。これを実装してみると、
mod = 998244353
N = 3*10**5 + 100
fact = [1]*(N+1)
factinv = [1]*(N+1)
for i in range(2, N+1):
fact[i] = fact[i-1] * i % mod
factinv[-1] = pow(fact[-1], mod-2, mod)
for i in range(N-1, 1, -1):
factinv[i] = factinv[i+1] * (i+1) % mod
I = [0] * (N+1)
I[0] = 1
I[1] = 1
for i in range(2, N+1):
I[i] = (I[i-1] + (i-1)*I[i-2]) % mod
T = int(input())
for _ in range(T):
n = int(input())
ans = 0
for k in range(n//4 + 1):
ans += fact[n-2*k]*factinv[k]%mod*factinv[n-4*k]%mod*I[n-4*k]
ans %= mod
print(ans)
こうなります。サンプルの の場合で正しいことが確かめられるので、エスパーに成功したと言ってもよいでしょう。実際、これを投げれば AC が出てきます!!!!!
まとめ
OEIS は謎の数列の正体を検索できるサイトです。競プロにおいては特に定数個入力の確率・数え上げ・総和の問題でよく効き、本質的な考察をスキップして問題の解法をエスパーできることがあります。OEISエスパーのだいたいの流れは次のようになります。
- 問題文を見る
- 少し考察しつつ愚直解を書く
- OEIS に入れる
- 解法を探したりエスパーする
- 実装する
最も多く時間を使うのは 3. と 4. です。問題によっては OEIS に載っておらず失敗することもあります。直接 OEIS でヒットしない場合、よく使えるテクニックとして、
- 第2項・第3項以降だけを検索する
- あえて特徴的な量で分解する
- なにかの値で加減乗除する
があります。
さいごに
OEIS エスパーは有用ですが、あまりに非教育的だったり、時間がかかってしまうことからあまりおすすめできません。しかし競プロerとして、他人に負けるくらいならエスパーも厭いません。それに、OEIS 自体はうまく使えば時短にもなります。OEIS を武器として戦いましょう!読んでくれてありがとうございました!
みなさん、これがtraP新歓ブログリレー2023の記事だということを忘れていませんか?明日は @Ras さん、 @toshi00 さんの記事(2本)です。見てね~!
