本記事はtraP夏のブログリレー8日目の記事です。
ちょっと遅れたけどセーフセーフ
この記事はtraP内で行われたらんぷろ(部内LT)の発表で用いたスライドを再構成したものです。
Tesseractとは
こんにちは、Fogrexです
四次元の超立方体(正式名称は正八胞体)のことです。
テッセラクトは空間を操るインフィニティーストーンの一種で、物体をどんなところへも瞬時に移動させる能力を持ちます。あとすさまじいエネルギーを持つので兵器開発に使われたりします。実際ヒドラはテッセラクトで当時の人類を超えたテクノロジーを手にしていました。
というのはMCU(Marvel Cinematic Universe)上の設定です。マーベルコミックを実写映画化したこのシリーズ、めっちゃ面白いので見てください(アイアンマンとかアベンジャーズとか聞いたことある人多いと思います。)
話を戻すと、テッセラクトは三次元空間での正六面体に相当する四次元の正多胞体です。下のWikipediaの記事を見たことある人も多いでしょう
https://ja.wikipedia.org/wiki/正八胞体
このWikipediaのページの中にあるGIFが結構有名ですよね。
これを描画してみようという話です。ちなみに過去にもやってます。

どうしましょう
WikipediaのGIFみたいなやつが結構よくやられる。どうして?
Wikipediaのあれは、いわゆるテッセラクトのワイヤフレームを行列を使って座標変換して表示しています。3Dの表示方法がわかっていると、その行列を4次元に拡張すればよいので結構簡単(諸説)にできます。また上の昔の僕の記事はレイマーチングなので行列を考えずに済み、さらに簡単にできます。
でも2次元より高次元の物体を描画する方法は2種類あります。上の行列による座標変換による描画が多次元をより低次元に投影しているという考え方(僕のレイマーチングの方式は4次元を3次元に投影してさらに2次元に投影しています。)なのに対して、もう一つの方法は、多次元を描画する低次元でスライスするという考え方をします。
前者の方式の四次元レンダリングはやっている人がたくさんいるので、ちょちょっとググってみてください。後者の方式の四次元レンダリングはやっている人がそう多くない、と思います。
後者の方式を使った有名なソフトウェアとして、4DToysがあります。
これはまさに後者の、「4次元を3次元でスライスする」方式をとっています。この開発者はMiegakureという4次元空間を舞台にしたパズルゲームを作っていて、それの技術を使って作られたのだと思います。このソフトの描画方法に関して、何をやっているかわからない人のために、4DToysがわかりやすく解説してくれています。
三次元物体を後者の方式で投影すると、ある平面でスライスした断面が見えます。当然ですね。高校数学でも散々やったと思いますが、三次元物体を二次元平面でスライスするというのはすぐ理解できると思います。じゃあ四次元を三次元でスライスしたら?当然三次元物体に投影されることになります。
四次元物体モデル表現
じゃあ四次元物体はどう表現しましょうか。初めから四次元物体について考えていてもわかりません。三次元で考えてみましょう。三次元物体を表現するときの最小単位は何でしょうか?モデリングしたことある人はわかると思いますが、三角形なわけです。いわゆるポリゴンですね。
うそつけ、モデリングするときは四角形とか五角形のポリゴンだって存在するぞ!だって?モデリングソフトの表示上は確かにそうかもしれませんが、結局内部では三角形で処理されています。当然ですね、異なる三点を通る平面はただ一つしか決まりませんから。
では四次元はどうでしょう。もうわかりましたね、最小単位は三角錐です。
断面
例にならい、また三次元物体の二次元平面でのスライスを考えましょう。三次元空間にある三角形を、例えばz=0の平面で切ってみましょう。

こういうことですね。頂点データを与えられるわけですから、z=0となる内分点を考えることができて、そうなる点は最大で二点あるので、その二点をつなげば線がかけるわけです。たとえx+4y+6z=0となるような平面で切る、みたいな話になったとしても、x+4y+6z=0がz=0となるように座標変換すれば同様にできます。ちなみに全部の点がz=0上にある時はまた別に処理する必要があります。
じゃあ四次元はどうでしょうか。ちょっとだけめんどくさいです。
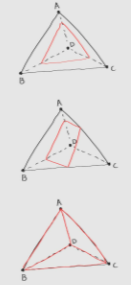
この3パターンがあります。雑で申し訳ない。最後の一つはメッシュが4枚に増えるんで簡略化のために実装では無視しました。ほんとはよくないから直さないといけないんですけどね。
断面の実装はシェーダーのジオメトリシェーダーでやりました。オブジェクト中に含まれる三角錐の数だけ頂点を用意し、各頂点に四点の座標を変数でシェーダーに渡しています。
モデリング
四次元物体のモデリングソフトなんてないので、プロシージャルに作る必要があります。正八胞体は三次元での正六面体に相当するという話をしました。正八胞体を正六面体と照らし合わせて考えましょう。
正六面体をプログラムで作ろうと思ったらどうしましょうか。正六面体はx,y,z軸に垂直な平面二つずつで構成されています。ということは、正八胞体ではx,y,z,w軸に垂直(?)な立方体二つずつで構成されるだろうという予想ができます。
ということは、正六面体を三角錐で表現して、それを八か所に並べればよいです。
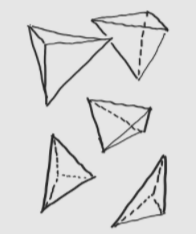
こんな感じで三角錐で正六面体が出来ますよね?あとは各軸を固定して生成しましょう。
出来た
以上の諸々を使ってできたゲーム(?)です。
Windowsのみビルドしてあります だれかMacかしてくれるならMac版も出せると思います。ただ4次元キューブを回して遊ぶだけですが、良かったら遊んでください。音がでかいかもしれないので気を付けて。
諸事情で遊べない人向けの動画は以下に置いておきます。
次回
明日はiroriさんの記事です。お楽しみに。


