こんにちは、@d_etteiu8383です。この記事はtraP夏のブログリレー9月6日の記事です。この記事ではBlenderにおけるVector Displacementとその悪用を紹介します(悪用がメインですので前半は飛ばしていただいても構いません)。

突然ですが本日9月6日が何の日だかご存じでしょうか？そうです、つい先日NonSugarとしての初のアルバム『Tasting NonSugar』を発売したことでも有名な真中のんさんの誕生日ですね。

彼女はアニメ『プリパラ』の登場人物の一人ですが、このアニメは3DCGを利用したライブシーンが特徴的ですよね。ということで本記事は3DCGに関するお話です。

ディスプレイスメントとは

3DCGにおけるディスプレイスメント(displacement)とは、(おおざっぱに言うと)モデル表面を変形させる操作・技術のことです。"displace"の意味そのまんま(移す、ずらす)ですね。

ディスプレイスメントの例

具体例を見てみましょう。以下はBlenderにおけるディスプレイスメントの利用例です。本記事では簡単にしか説明しません。詳細は公式のドキュメントを確認してください→Displacement — Blender Manual

説明用に下の画像のようなUV球を用意しました。わかりやすさのために、市松模様の色付けと辺の表示を行っています。

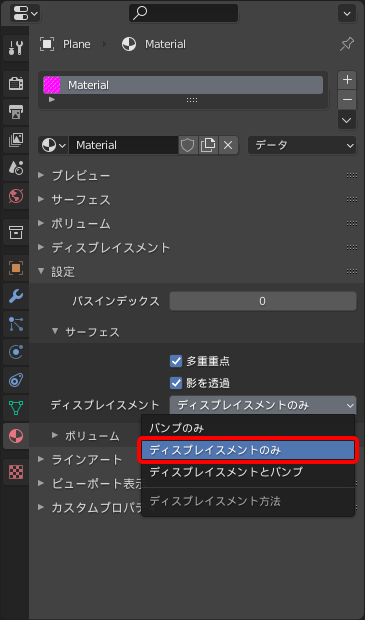
早速ディスプレイスメントを利用してみましょう。Blenderにおいてはモディファイア―でのディスプレイスメントと、マテリアルでのディスプレイスメントの2種が利用できますが、今回はマテリアルからのディスプレイスメントを利用します。まず、下記画像のようにマテリアルプロパティの"設定"→"サーフェス"→"ディスプレイスメント"を"ディスプレイスメントのみ"に設定し、ディスプレイスメントを有効化しましょう。ここが"バンプのみ"になっているとディスプレイスメントが反映されません。(参考：Displacement#Displacement Only — Blender Manual)

これでマテリアルからディスプレイスメントを扱えるようになりました。早速簡単な例を試してみましょう。

マテリアル出力：ディスプレイスメント

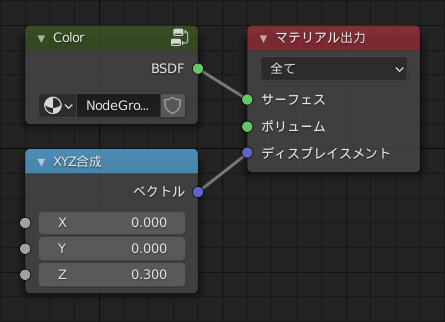
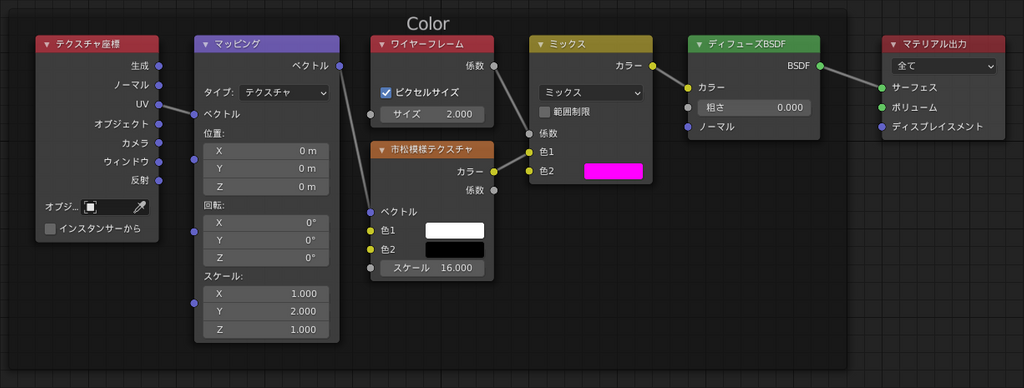
まずマテリアル出力ノードのディスプレイスメントに[0.0, 0.0, 0.3]のベクトルを入力として与えてみます。(参考：Material (マテリアル出力)ノード — Blender Manual)(サーフェスに与えている値は無視してください。先述した色の設定をまとめただけです。)

すると、もともとのUV球の位置(画像中オレンジの線)から少し上にずれた位置にUV球がレンダリングされます。

これがディスプレイスメントの最も簡単な例です。与えられたベクトルの値だけ、頂点位置を移動させるのがディスプレイスメントです。この例では、UV球のすべての頂点が[0.0, 0.0, 0.3]だけ移動したので、Z軸方向に(つまり画像の上方向に)UV球が移動したわけです。もし代わりに[0.5, 0.0, 0.0]のベクトルを与えればX軸方向に移動するのもお分かりいただけると思います。

次に、少しだけ発展した例を紹介しましょう。

上図のようにマテリアルを設定すると、UV球の右半分が右上に移動します。各ノードを順に追って仕組みを理解しましょう。ちょっと長いので上のノードツリーを見てやっていることが理解できる方は下まで読み飛ばしていただいて構いません(下までスキップする)。

まず図中一番左のジオメトリノードの"位置"の出力を、XYZ分離ノードの"値"に入力しています。ディスプレイスメントは各頂点に対して行われるものなので、ここでのジオメトリノードの"位置"出力は各頂点の位置を出力していると考えてください(厳密には違うけど言語化が難しい)。XYZ分離ノードはその名の通り、入力として与えられたベクトルのそのX,Y,Zの値を別々のスカラーに分離して出力します。
(参考：Geometry (ジオメトリ)ノード — Blender Manual, Combine/Separate (合成/分離)ノード — Blender Manual)

上図の例では各頂点のX座標を用いたかったので、X座標のみを取り出して次のノードに渡しています。

そのX座標を、"大きい"ノードの"値"の入力に渡しています。これは"値"が"しきい値"よりも大きい場合は1を、それ以外の場合は0を出力するノードです。
(参考：Math (数式)ノード #Greater Than — Blender Manual)

上図の例では、頂点のX座標が0.05よりも大きい場合は1を、それ以外の場合は0を出力していることになります。

次にこの値を乗算ノードに渡しています。これもその名の通り、入力の値を乗算して出力するノードです。上図の例では入力の値を0.2倍しています。
(参考：Math (数式)ノード #Multiply — Blender Manual)

最後にこの値を、XYZ合成ノードに渡しています。これはXYZ分離ノードの逆の働きをするノードで、入力として与えられた3つのスカラーを要素とする1つのベクトルを出力します。
(参考：Combine/Separate (合成/分離)ノード — Blender Manual)

以上をまとめると、

• X座標が0.05よりも大きい場合はマテリアル出力のディスプレイスメントに[0.2, 0.0, 0.2]を入力する
• X座標が0.05以下の場合はマテリアル出力のディスプレイスメントに[0.0, 0.0, 0.0]を入力する

といったノードツリーになっています。これにより、「右半分(X座標が0.05以上)の頂点は少し右上([0.2, 0.0, 0.2])に移動し、それ以外の頂点は移動しない」というディスプレイスメントが行われます。

ここで、Blenderにおけるディスプレイスメントはあくまでも頂点を移動させるものであることに注意しなければなりません。

頂点ではなく表面全体が先述の条件で移動した場合は、上図右の画像のようになりますが、通常はそうはなりません。「ディスプレイスメントは頂点を移動させるもの」と覚えておきましょう。

上の例ではマテリアル出力のディスプレイスメント入力に直接ベクトルを入力していましたが、もう少し手軽にディスプレイスメントを扱うためのノードが2つ用意されているので、以下で説明します。

ディスプレイスメントノード

ディスプレイスメントノードは、入力として"高さ"と"ノーマル(法線)"を受け取り、「その法線に沿って、その高さ分頂点を移動させる」ようなディスプレイスメントをするためのベクトルを出力するノードです。
(参考：Displacement (ディスプレイスメント)ノード — Blender Manual)

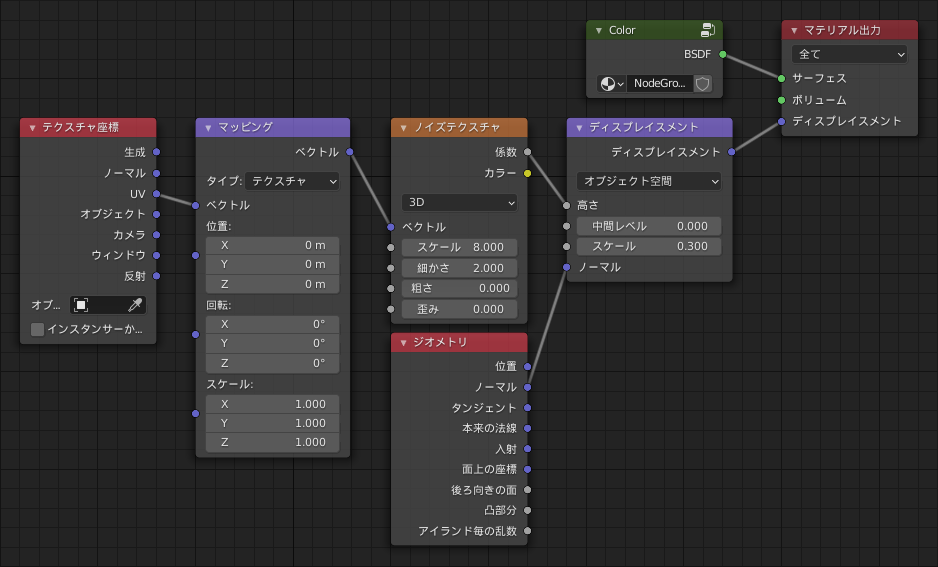
例えば下図左の画像のようにノードを組むと、ディスプレイスメントノードからは「本来のモデルの法線にそって、高さ 0.1 だけ移動する」ディスプレイスメントをするためのベクトルが出力されます。そのため、下図右の画像のように、元のUV球から少し膨らんだような(=法線に沿って全頂点が 0.1 だけ移動した)結果が得られます。

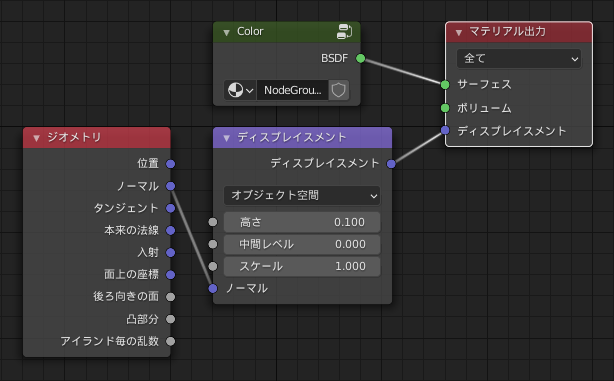
また、"高さ"にノイズテクスチャや画像からの値を渡すことで、でこぼこした表面を表現したり、頂点毎の変位を手軽にコントロールすることができます。

ベクトルディスプレイスメントノード

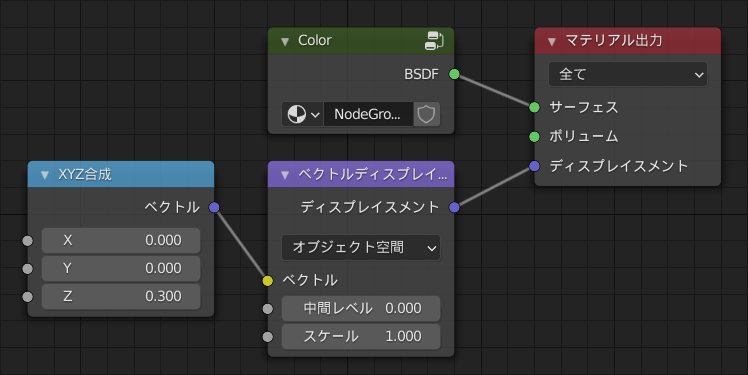
ベクトルディスプレイスメントノードは頂点を法線に沿って移動するディスプレイスメントノードと異なり、任意の方向に移動させることができます。...つまり最初に説明した、ベクトルを直接マテリアル出力ノードに繋ぐ方法とほとんど同じです。ベクトルディスプレイスメントノードを利用することで、適用する空間(オブジェクト空間での変形か、ワールド空間での変形か、タンジェント空間での変形か)を変更することができたり、中間レベル(変位の基準値)やスケール(変位の強さ)を設定できて色々便利です。

ディスプレイスメントの利用例

ここまでディスプレイスメントについて説明してきましたが、究極的に言ってしまえば「モデル自体を編集してしまえば頂点の移動はできる」ため、その恩恵は小さいように感じてしまいます。が、それは大きな間違いです。ディスプレイスメントにはディスプレイスメントなりのメリットが多々存在します。

テクスチャで使いまわせる

ディスプレイスメントノードでは高さを入力としていましたが、この"高さ"の値を保存した配列を画像として保存しておけば、さまざまな場面で利用することができます。

例えば下図左の画像はambientCGというフリーのマテリアル素材を配布しているサイトから拝借した岩のマテリアル(Rocks 011 on ambientCG)のディスプレイスメントテクスチャです。これをディスプレイスメントノードの"高さ"に接続することで、下図右のような結果が得られます(UV球に適用した場合)。このように、画像としてディスプレイスメントのデータを保持しておけば、さまざまな形状のモデルに対して同様に表面の変形をさせることが可能です。

非破壊的である

今回紹介した例ではすべて同一のUV球を使いまわしていましたが、変更したのはマテリアルのみで、UV球のモデルデータ自体には一切手を加えていませんでした。平面や球面など、元の形状を保っておきたい時に便利です。

ディスプレイスメントの悪用

ここからがこの記事の本番です。上でディスプレイスメントについて、「モデルを変形させる技術」と説明しました。

...モデルを変形することができるなら、ディスプレイスメントだけでモデリングができるのではないでしょうか？

ということでやりましょう。

適応サブディビジョンの利用

blenderにおけるディスプレイスメントでは頂点のみを移動させることができました。逆に言うと、元のメッシュの頂点数が少ないと、どんなに精巧なマテリアルを用意しても良い結果は得られません。頂点数が実質的なモデルの"解像度"になってしまいますからね。そこで、今回は適応サブディビジョン(adaptive subdivision)を利用します。(参考：Adaptive Subdivision — Blender Manual)

そもそもサブディビジョンはメッシュを分割することを指しますが(参考：Subdivision Surface Modifier — Blender Manual)、適応サブディビジョンではその分割を"適応的に"行います。つまり「カメラに近い領域は最終的に大きく見える部分なので細かく分割し、カメラから遠い領域は最終的に小さく見える部分なのでおおざっぱに分割」します。

下図は、画面右下にカメラを設置した場合の平面の分割を示したものです。白線が適応サブディビジョンによって生成された辺であり、カメラに近い領域(=右下)に近づくにしたがって分割が細かくなっているのがわかると思います。

この適応サブディビジョンを用いることで頂点数の多いモデルを無理やり作成し、ディスプレイスメント結果をきれいにしようという作戦です。

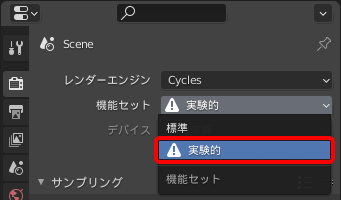
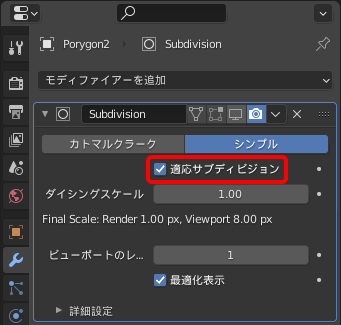
適応サブディビジョンは"レンダープロパティ"で"レンダーエンジン"としてCyclesを選び、機能セットを"実験的"にした場合のみ利用でき、モディファイアーにサブディビジョンを追加して"適応サブディビジョン"にチェックを付けることで有効化できます。

UV球にノイズテクスチャで凹凸を付けた先ほどの例で、適応サブディビジョンの"強さ"を確認してみましょう。下図左の画像は元のUV球のままディスプレイスメントを行った結果で、右の画像は適応サブディビジョンを適用した状態でディスプレイスメントを行った結果です。

適応サブディビジョンを行っている方では、メッシュが非常に細かく分割されてそこらじゅう頂点だらけになっているので、ノイズテクスチャがほぼそのまま表面に現れていますね。

これを使ってディスプレイスメントで遊んでいきましょう。

ディスプレイスメントでモデリング

今回の目標は「1ポリゴンでポリゴン2を作る」です。カクカクのポリゴンが進化した姿である点、人工のポケモンである点、簡単すぎず複雑すぎない滑らかなフォルムである点がディスプレイスメント遊びにぴったりです。決してダジャレで選んだわけではありません。

ポリゴン２｜ポケモンずかん

『ポケットモンスター』シリーズに登場するポケモンの情報を見ることができる、「ポケモンずかん」。

ポケモンずかん

1ポリゴン→UV座標

3DCGにおける"1ポリゴン"は三角形です。これを無理やり変形してポリゴン2にしたいわけですが、三角形のまま扱うのは少し不便です。まずは扱いやすい四角形に変形することから始めます。四角形と言ってもただの四角形ではありません。左下が(0, 0)、右上が(1, 1)の位置の情報を持つような正方形、つまりUV座標系を手に入れましょう。

まず、以下のような"1ポリゴン"を用意しました。

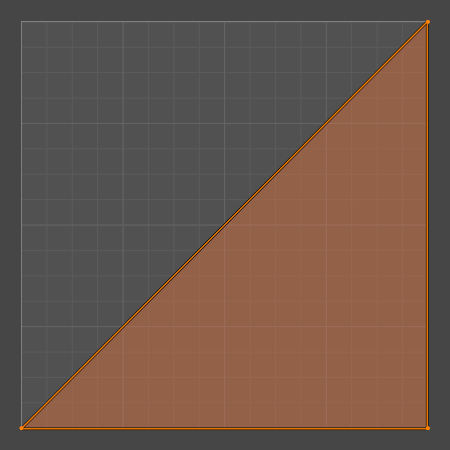
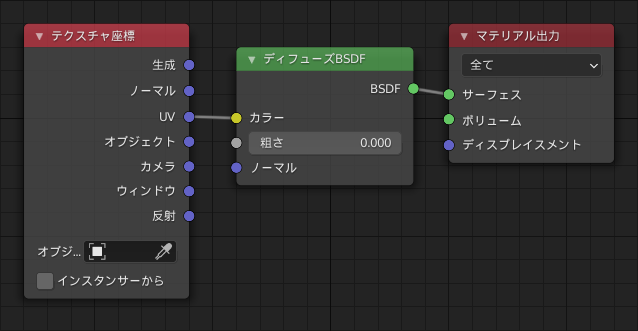
何の変哲もない1ポリゴンです。中央の画像のようにUV展開し、右画像のマテリアルでUV座標をそのまま色としています(Blenderでは3次元の座標データベクトル(x, y, z)を3次元の色のデータ(R, G, B)に暗黙的に型変換できる 参考：ノードを構成するパーツ — Blender Manual)。

このUV展開を見てわかるように、この1ポリゴンには(0, 1)や(0.2, 0.7)等のUV座標($x<y$となるような$(x,y)$)が含まれません。欲しいのは$[0,1]\times [0,1]$の座標系です。ということでこの三角形に$[0,1]\times [0,1]$の座標系を無理やり押し込むことを考えます。

三角形内のUV座標$(u,v)$に対し、

$$\{\begin{array}{ll}{u}^{\prime }& =u-\min (1-u,v)\\ v^{\prime }& =v+\min (1-u,v)\end{array}$$

と計算して得られる$(u^{\prime },v^{\prime })$は$[0,1]\times [0,1]$になります。

これで3角形の領域内と$[0,1]\times [0,1]$を一対一対応させることができますね。...導出過程は面倒なので説明しません。

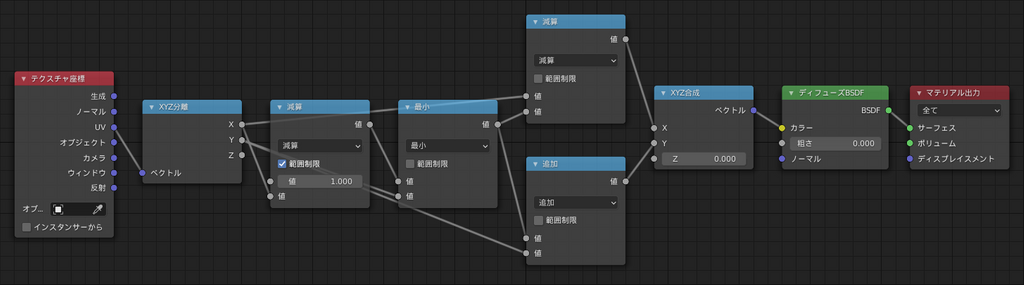
簡単に説明すると、「正方形の左上部分をグイっと右下方向に押しつぶして三角形にした」感じです。

とにかくこれで便利なUV座標を得ることができました。ここから先の説明で登場する$(u,v)$はいわゆる普通のUV座標で、$[0,1]\times [0,1]$内の点であると考えてください。また、この「三角形からUV座標を作るノード」は今後使いまわしたいのでグループ化しておきましょう。

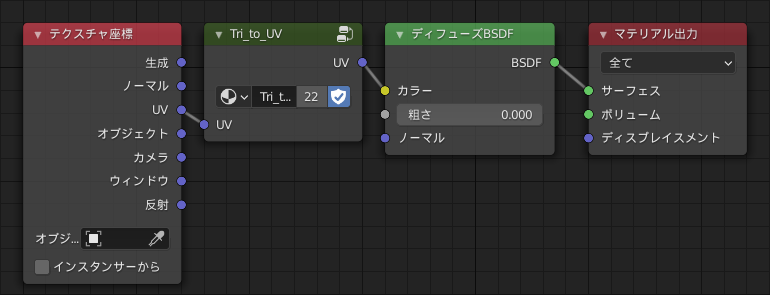
UV座標→プリミティブな図形

UV座標を得ることができたので、次は簡単な図形を作成してみましょう。目標は「Blenderで追加できるプリミティブなメッシュ(のうちICO球以外)の図形をディスプレイスメントで表現する」です。

元の"1ポリゴン"上の点を、そのUV座標$(u,v)$から計算された空間上の点$(x,y,z)$に移動させることで図形を表現することにしましょう。そのために、以下のような補助ノードグループを作成しました。

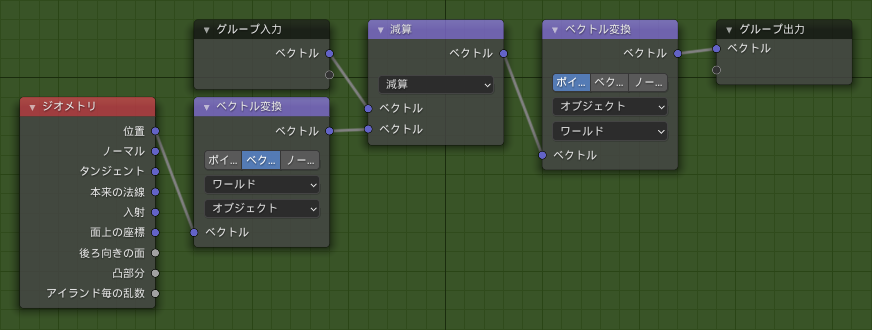
本来のディスプレイスメントでは、例えば(0.0, 0.0, 0.3)といったベクトルが入力された場合、もともとの頂点の位置から相対的に(0.0, 0.0, 0.3)だけ頂点が移動するようになっています。これでは少し不便なので、「(0.0, 0.0, 0.3)を与えられたらその頂点は(0.0, 0.0, 0.3)に移動する」という、もともとの頂点の位置を無視して絶対的な頂点移動を行うためのノードグループを作成しました。

それではこれを利用して図形を作っていきましょう。

正方形

これは一番簡単そうですね。$xy$平面上に存在し、一辺の長さが$s$の、原点を中心とするような正方形をUV座標から作ることを考えましょう。

...考えましたか?答えはこんな感じ。(今後導出過程は説明しません。言語化が難しい。)

$$\{\begin{array}{ll}x& =s(u-0.5)\\ y& =s(v-0.5)\\ z& =0\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら。

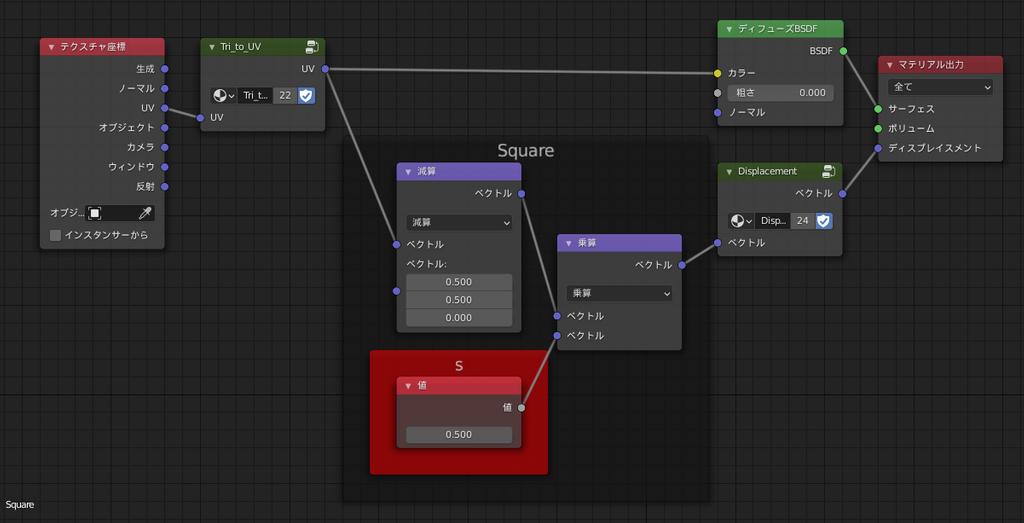
綺麗な正方形になっていますね。こんな感じでひたすら計算により図形を作っていきます。

円柱

底面が$xy$平面上に存在する、高さ$h$、半径$r$の円柱を作ります。と言っても上下の面を作るのは面倒なのでとりあえず側面を作ってみます。計算するとこんな感じ。

$$\{\begin{array}{ll}x& =r\cos (2\pi u)\\ y& =r\sin (2\pi u)\\ z& =hv\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら(ノードが複雑になってきて画像を見せる意味が無くなってきたので割愛)。

このディスプレイスメントのイメージとしてはこんな感じ。

以下、こんなの説明してもだれも読まないだろって感じなので折りたたみます。詳細をみたい方はクリックしてページを展開してください。

円錐

円錐

底面が$xy$平面上に存在する、高さ$h$、半径$r$の円錐。

$$\{\begin{array}{ll}x& =r(1-v)\cos (2\pi u)\\ y& =r(1-v)\sin (2\pi u)\\ z& =hv\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら。

円

円

高さ0の円錐を考えればよいので、円錐の計算で$h=0$とすればよい。

角柱

底面が$xy$平面上に存在する正$N$角形であるような、高さ$h$、半径$r$の角柱。一見複雑ですが多角形の頂点位置を計算して間に平面を張ってるだけ。

$$\{\begin{array}{ll}x& =r\left(\left(Nu-\lfloor Nu\rfloor \right)\cos (\frac{2\pi }{N}\lfloor Nu\rfloor )+\left(1-\left(Nu-\lfloor Nu\rfloor \right)\right)\cos (\frac{2\pi }{N}\lfloor Nu+1\rfloor )\right)\\ y& =r\left(\left(Nu-\lfloor Nu\rfloor \right)\sin (\frac{2\pi }{N}\lfloor Nu\rfloor )+\left(1-\left(Nu-\lfloor Nu\rfloor \right)\right)\sin (\frac{2\pi }{N}\lfloor Nu+1\rfloor )\right)\\ z& =hv\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら。

角錐

角錐

底面が$xy$平面上に存在する正$N$角形であるような、高さ$h$、半径$r$の角錐。

$$\{\begin{array}{ll}x& =r\left(1-v\right)\left(\left(Nu-\lfloor Nu\rfloor \right)\cos (\frac{2\pi }{N}\lfloor Nu\rfloor )+\left(1-\left(Nu-\lfloor Nu\rfloor \right)\right)\cos (\frac{2\pi }{N}\lfloor Nu+1\rfloor )\right)\\ y& =r\left(1-v\right)\left(\left(Nu-\lfloor Nu\rfloor \right)\sin (\frac{2\pi }{N}\lfloor Nu\rfloor )+\left(1-\left(Nu-\lfloor Nu\rfloor \right)\right)\sin (\frac{2\pi }{N}\lfloor Nu+1\rfloor )\right)\\ z& =hv\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら。

正多角形

正多角形

高さ0の角錐を考えればよいので、角錐の計算で$h=0$とすればよい。

UV球

UV球

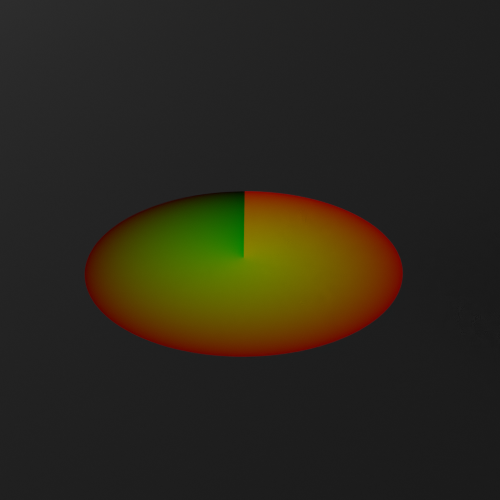
半径$r$の球。球面座標系から3次元のデカルト座標系への変換と同じですね。球面と平面を対応させる感じ。

$$\{\begin{array}{ll}x& =r\sin (\pi v)\cos (2\pi u)\\ y& =r\sin (\pi v)\sin (2\pi u)\\ z& =r\cos (\pi v)\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら。

トーラス

トーラス

大半径が$R$、小半径が$r$であるようなトーラス。良い感じに計算する。

$$\{\begin{array}{ll}x& =R\cos (2\pi u)+r\cos (2\pi u)\cos (2\pi v)\\ y& =R\sin (2\pi u)+r\sin (2\pi u)\cos (2\pi v)\\ z& =r\sin (2\pi v)\end{array}$$

これをノードで表現し、ディスプレイスメントを行った結果がこちら。

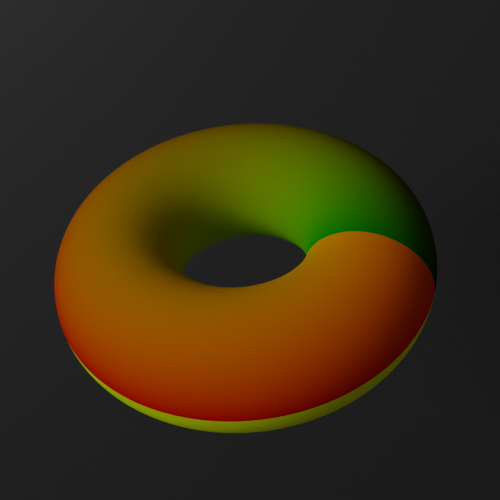
これで様々な図形を1ポリゴンで表現できるようになりました。..."1ポリゴンで"とはいってもレンダリング時には適応サブディビジョンにより数千ポリゴンになってはいるのですが、まあ実質1ポリゴンです。

ノードに与える値はキーフレームが打てるのでノードだけでアニメーションさせることも可能です。

UV→複数のUV

三角形からUV座標を生み出すことには成功しましたが、このままでは1つのUV座標しか利用できません。次は複数のUV座標を生み出しましょう。正の整数$W,H$に対し、

$$\{\begin{array}{ll}{u}^{\prime }& =Wu-\lfloor Wu\rfloor \\ v^{\prime }& =Hv-\lfloor Hv\rfloor \end{array}$$

として新たなUV座標$(u^{\prime },v^{\prime })$を計算すると、横に$W$個、縦に$H$個の$[0,1]\times [0,1]$の区間が生まれます。それぞれ$W$倍、$H$倍して小数部を取る感じです。

下の動画のように、UV座標を分割し、それぞれを変形させつつ間を透明にすることで複数の図形を作成することができました。

ここまで来ればポリゴン2の完成も目前です。

ポリゴン2の形状作成

ポリゴン2のパーツをプリミティブで再現していきましょう。頭・胴・手足はUV球を、首と尻尾は円柱を応用することでできそうです。

プリミティブを組み合わせて概形を作成しましたが、本物のポリゴン2は首と尻尾がくびれているのでそれも再現したいですね。これは適当な関数$r(t)$を用意して、円柱の式を

$$\{\begin{array}{ll}x& =r(v)\cos (2\pi u)\\ y& =r(v)\sin (2\pi u)\\ z& =hv\end{array}$$

とすることで実現できそうです。Blenderのマテリアルノードで関数(というか曲線)が欲しいとき、奥の手としてRGBカーブノードを利用することができます。(参考：RGB Curves ノード — Blender Manual)

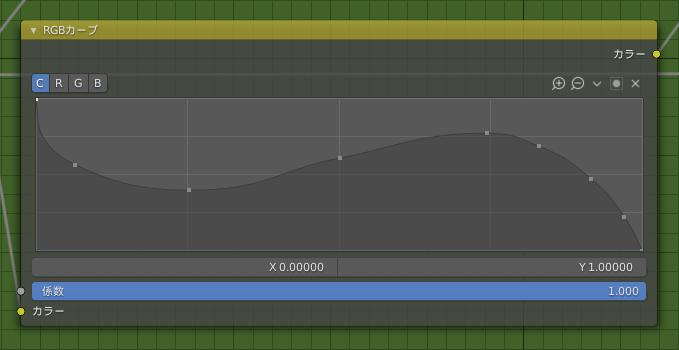
本来は色補正のために用いるノードであり、いわゆるトーンカーブなのですが、入力する色を[0, 1]の変数、出力される色を従属変数と見なすことで関数のように扱うことができます。これを使い、ポリゴン2と尻尾のくびれを表現しました。

これでポリゴン2の形が完成しました。あとは色を付けたりライティングを調整するだけです。が、ディスプレイスメントには関係ない部分なのでサクッとやっちゃいます(説明がめんどくさかった)。

ということで「1ポリゴンからポリゴン2を作る」ことができました。元が1ポリゴンなだけでもちろん適応サブディビジョンで数千ポリゴンになっている。

最終的なノードは以下のようになりました(実際にはグループ化して作業しやすくしていますが、下図ではすべてのグループ化を解除しています)。

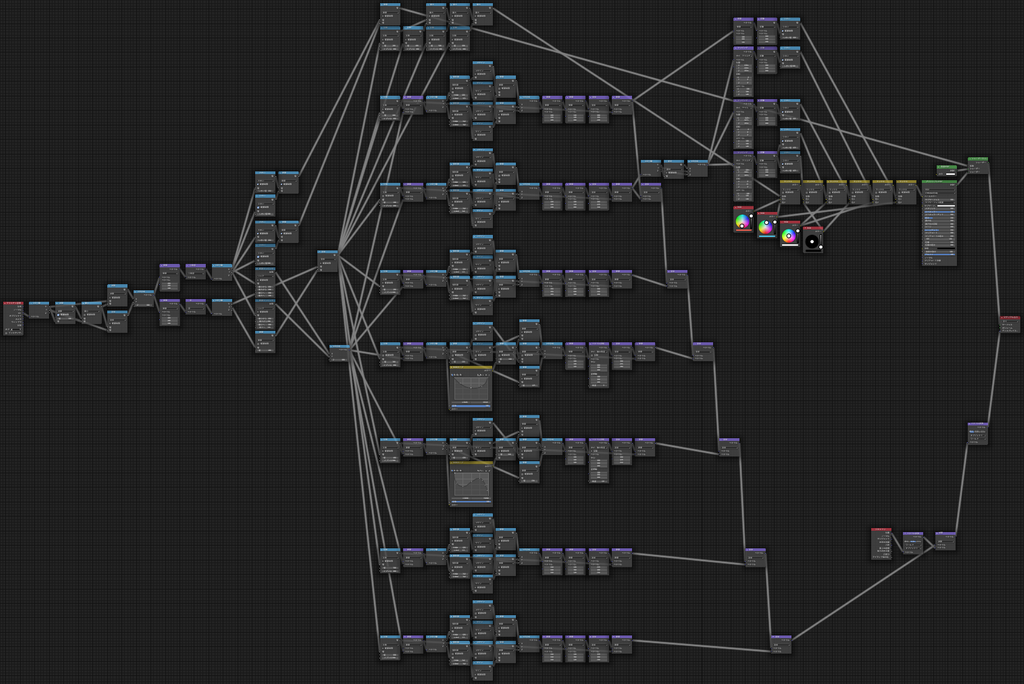
Blenderに標準で備わっているノードのみ利用しています。ノード数は...

184個らしい。意外と少ない。(上の動画のアニメーションを表現するためのマテリアルではもっとノードを使っている)

ディスプレイスメントでここまでやる必要は全くありませんが、「こういうこともできるんだよ」というお遊びでした。数式で図形を表すことができるので、メビウスの輪のような「正確にモデリングしようと思うと少し面倒な物」とかを手軽に作れて意外と便利だったりもします。↓これ↓とかも今回説明した適応サブディビジョンとディスプレイスメントで作ってます。

皆さんもぜひ色々チャレンジしてみてください。シェーダーノードの勉強にもなるのでオススメです。実は今日紹介したテクニックはNodevemberというイベントで多用されています。このイベントについて紹介した記事も過去に執筆しているので、良ければそちらもご覧ください。

プロシージャルの世界へ~NovemberはNodevember~

この記事はtraPアドベントカレンダー2020 7日目(11/20)の記事です。 -------------------------------------------------------------------------------- 19のでっていう(@d_etteiu8383 [/author/d_etteiu8383/])です。普段は3DCGで遊んだりしてます。本記事ではBlenderにおけるプロシージャルマテリアルとNodevemberというイベントについてご紹介したいと思います。 なお、この記事ではBlenderのノードエディタの細かい操作の解説はしていません。あ…

東京工業大学デジタル創作同好会traPd_etteiu8383

少々わかりにくい記事になってしまいましたが、最後までお読みいただきありがとうございました。明日のブログリレー担当者は@iroriさんです。楽しみ～