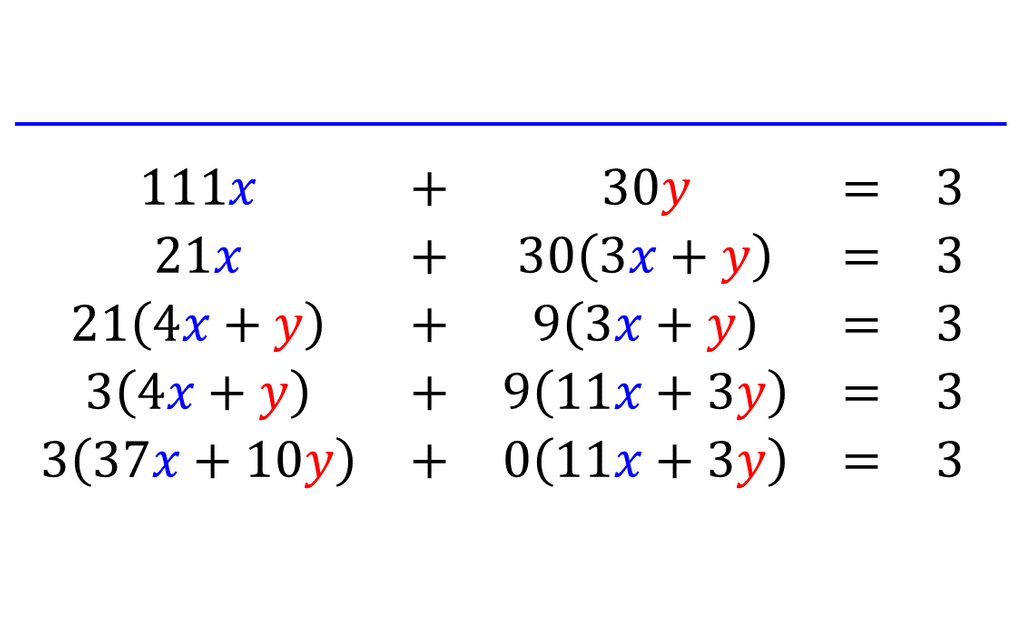ベズー係数とN項の拡張ユークリッドの互除法

こんにちは、すく(0214sh7)です
東工大数学系の3年生で、traPではアルゴリズム班のリーダーをやっています。

本来この時期にブログを書くつもりはなかったのですが、唐突にベズー係数すきすき侍と化したので筆をとりました。

拡張ユークリッドの互除法とは？

競技プログラミングをやっている中で拡張ユークリッドの互除法(extended Euclidean algorithm)の存在を知った人は多いと思います。
機能としては通常のユークリッドの互除法の拡張になっています。
けんちょんさんのqiita記事などで丁寧に解説されていますので、この記事では詳しく解説しません。

ベズー係数

a x + b y = g c d (a, b)

これはベズーの等式(Bézout's identity)と呼ばれる式です。
フランスの数学者エティエンヌ･ベズーからこの名前がつきました。
ベズーの等式にまつわる定理として、ベズーの補題(Bézout's lemma)があります。この定理は以下を主張しています

$a, b$ を0でない整数、 $d$ を $g c d (a, b)$ とする。このとき、１次方程式

a x + b y = c

は、 $c$ が $d$ の倍数であれば無数の整数解を持ち、 $c$ が $d$ の倍数でなければ整数解を持たない。

証明(クリックで開く)

まずは $c$ が $d$ の倍数でなければ整数解は存在しないことを示したい。
$a$ は $d$ の倍数であるので、整数 $h$ が存在して $a = h d$ である。
同様に、整数 $k$ が存在して $b = k d$ である。
すると、 $a x + b y = (h x + k y) d$ である。 $x, y$ が整数だとすれば $h x + k y$ も整数であるので、 $a x + b y$ は $d$ の倍数である。
このため、 $c$ が $d$ の倍数でなければ $a x + b y = c$ を満たす整数 $(x, y)$ は存在しない。

次に $c$ が $d$ の倍数であれば整数解を1つ持つことを示したい。
ここで、 $a r + b s = d$ を満たす整数 $(r, s)$ が存在することを用いる。補題として以下に示す。

補題の証明(クリックで開く)

一般性を失わず $a, b > 0$ とする。
$a_{0} : = a, b_{0} : = b$ 、 $i \geq 0$ として、 $a_{i} = b_{i} q_{i} + r_{i} (0 \leq r_{i} < b_{i})$ をみたす $q_{i}, r_{i}$ が $b_{i} \neq = 0$ である限り存在する。そこで、 $a_{i + 1} : = b_{i}, b_{i + 1} : = r_{i}$ と定義する。
$b_{i} = 0$ をみたす最小の $i$ (存在する)を $k$ とすると、 $a_{k} = d$ である。
これより、 $a_{k} x + b_{k} y = d$ をみたす $(x, y)$ として $(1, 0)$ が存在することがわかる。

$a_{i + 1} z + b_{i + 1} w = d$ をみたす $(z, w)$ が存在すると仮定すると、 $a_{i + 1} z + b_{i + 1} w = b_{i} z + r_{i} w = b_{i} z + (a_{i} - b_{i} q_{i}) w = a_{i} w + b_{i} (z - q_{i} w) = d$ より、 $a_{i} x + b_{i} y = d$ をみたす $(x, y)$ として $(w, z - q_{i} w)$ が存在する。
これを再帰的に適用することで、 $a_{0} x + b_{0} y = d$ を満たす $(x, y)$ の存在が言える。

また、 $c$ は $d$ の倍数であるので、整数 $e$ が存在して $c = e d$ である。
すると、整数 $(e r, e s)$ が存在し $a (e r) + b (e s) = e d = c$ を満たすため、確かに整数解としてふさわしい。

そして整数解が1つあれば無数にあることを示したい。
これは難しくない。 $(x_{0}, y_{0})$ が整数解であれば $a x_{0} + b y_{0} = c$ であるのでこれを変形して $a (x_{0} + \frac{b}{d}) + b (y_{0} - \frac{a}{d}) = c$ 。よって $(x_{0} + \frac{b}{d}, y_{0} - \frac{a}{d})$ が整数解になる。
これを好きなだけ繰り返すことでいくらでも異なる整数解を生成できる。よって整数解は無数にあると言える。

証明は省略するが、特殊解 $(x_{0}, y_{0})$ と整数 $t$ を用いて $(x_{0} + t \frac{b}{d}, y_{0} - t \frac{a}{d})$ と表せる解が、方程式 $a x + b y = c$ の解のすべてである。

このことから $d$ は $a x + b y = c$ に整数解 $(x, y)$ が存在する $c$ の中で絶対値最小であり、任意の $c$ は $d$ の倍数である、ということが言えます。

ということなので、 $a x + b y = d$ をみたす $(x, y)$ を $(a, b)$ のベズー係数(Bézout coefficients)と名付けます(一意ではないことに気をつけてください)。

このベズー係数を1つ見つけることができるアルゴリズムとして知られているのが、拡張ユークリッドの互除法なのです！
最大公約数を求めるアルゴリズムであるユークリッドの互除法に機能を追加してベズー係数を求められるようにしていることから、この名前がつきました。

ここで驚くべき性質があります。拡張ユークリッドの互除法が与えるこのベズー係数 $(x, y)$ はなんと、

∣ x ∣ \leq ∣ ∣ ∣ ∣ ∣ \frac{b}{d} ∣ ∣ ∣ ∣ ∣, ∣ y ∣ \leq ∣ ∣ ∣ ∣ \frac{a}{d} ∣ ∣ ∣ ∣

をみたす2つのうち1つであるのです！

証明(クリックで開く)

帰納法を用いる。

一般性を失わず $a > b > 0$ とする。
まず拡張ユークリッドの互除法を実行して $b = 0$ に至る直前のステップ、つまりある $q \geq 1$ があって $a = q d, b = d$ という場合を考える。
この場合与えられるベズー係数は $(0, 1)$ であるので、 $∣ 0 ∣ \leq ∣ ∣ ∣ \frac{d}{d} ∣ ∣ ∣, ∣ 1 ∣ \leq ∣ ∣ ∣ ∣ \frac{q d}{d} ∣ ∣ ∣ ∣$ よりOK。

次に $b z + r w = d$ を満たす $(z, w)$ が条件を満たしていたと仮定した場合に $a x + b y = d$ を満たす $(x, y)$ が条件を満たすこと、すなわち $a = b q + r, x = w, y = z - q w$ として

∣ z ∣ \leq ∣ ∣ ∣ ∣ \frac{r}{d} ∣ ∣ ∣ ∣, ∣ w ∣ \leq ∣ ∣ ∣ ∣ ∣ \frac{b}{d} ∣ ∣ ∣ ∣ ∣ \Rightarrow ∣ x ∣ \leq ∣ ∣ ∣ ∣ ∣ \frac{b}{d} ∣ ∣ ∣ ∣ ∣, ∣ y ∣ \leq ∣ ∣ ∣ ∣ \frac{a}{d} ∣ ∣ ∣ ∣

を示す。
$∣ x ∣ = ∣ w ∣ \leq ∣ ∣ ∣ \frac{b}{d} ∣ ∣ ∣$ より、 $∣ x ∣ \leq ∣ ∣ ∣ \frac{b}{d} ∣ ∣ ∣$
$∣ y ∣ = ∣ z - q w ∣ \leq ∣ z ∣ + ∣ q w ∣ = ∣ ∣ ∣ \frac{r}{d} ∣ ∣ ∣ + ∣ ∣ ∣ ∣ \frac{q b}{d} ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ \frac{q b + r}{d} ∣ ∣ ∣ ∣ (∵ b q > 0, r > 0) = ∣ ∣ ∣ \frac{a}{d} ∣ ∣ ∣$
より、 $∣ y ∣ \leq ∣ ∣ ∣ \frac{a}{d} ∣ ∣ ∣$

以上より、機能法を用いて拡張ユークリッドの互除法が与えるベズー係数が

∣ x ∣ \leq ∣ ∣ ∣ ∣ ∣ \frac{b}{d} ∣ ∣ ∣ ∣ ∣, ∣ y ∣ \leq ∣ ∣ ∣ ∣ \frac{a}{d} ∣ ∣ ∣ ∣

を満たすものであることが示された。

2項のベズー係数を拡張ユークリッドの互除法を用いて計算できること、わかっていただけましたか？
C++による実装例はこちらから見れます。

3項でのベズー係数

ここからが本題です
N項での議論をする前に前準備として3項での議論をしようと思います。
実はベズー係数は3項としてもその存在が言えます。つまり、 $a, b, c$ を0でない整数として

a x + b y + c z = g c d (a, b, c)

をみたす整数(x,y,z)が存在します(そして $g c d (a, b, c)$ はそれを存在たらしめる右項のうち絶対値最小)。

これは次のようにして存在証明・計算ができます。

$(a, b)$ のベズー係数 $(p, q)$ を拡張ユークリッドの互除法を用いて一つ求める。
$(g c d (a, b), c)$ のベズー係数 $(r, s)$ を拡張ユークリッドの互除法を用いて一つ求める。
$(p r, q r, s)$ が $(a, b, c)$ のベズー係数の一つである。

これが何故かというと、
$(p, q), (r, s)$ の定義より、 $a p + b q = g c d (a, b)$ と $g c d (a, b) r + c s = g c d (g c d (a, b), c) = g c d (a, b, c)$ が成り立ち、2つ目の式の最初の部分に1つ目の式を代入することで、

(a p + b q) r + c s = g c d (a, b, c)

を導けるからです。
$a p r + b q r + c s = g c d (a, b, c)$ なので、 $(p r, q r, s)$ はベズー係数の定義を満たしています。

N項でのベズー係数

書いてて思ったんだけどニッチすぎませんか？競プロですら出てくるか怪しいぞ

3項のものと同様の手順でN項に拡張できます。
最後の1項を除くN-1項のベズー係数が見つかっているものとします。
つまり、 $(X_{1}, . ., X_{N - 1})$ が $(A_{1}, . ., A_{N - 1})$ のベズー係数の一つであることがわかっているものとします。また、 $d = g c d (A_{1}, . ., A_{N - 1})$ とします。

$(d, A_{N})$ のベズー係数 $(p, q)$ を拡張ユークリッドの互除法を用いて一つ求める
$(p X_{1}, p X_{2}, . . ., p X_{N - 1}, q)$ が $(A_{1}, . ., A_{N})$ のベズー係数の一つである。

3項のものと同じ理屈でこれでベズー係数を求められることがわかります。
$N = 1$ のときは $A_{1} x = A_{1}$ を満たせばよいので、ベズー係数は $1$ としておくとよいでしょう。

これをするコードを書いてみましょう。

ソースコード

import math

def bezout(a,b):
    if b==0:
        return [1,0]
    r = a%b
    q = (a-r)//b
    
    d = bezout(b,r)
    D = [d[1],d[0]-q*d[1]]
    return D
    
def bezoutN(A):
    if len(A)<=0:
        return []
    X = [1]
    g = A[0]
    for i in range(len(A)):
        if i==0:
            continue
        B = bezout(g,A[i])
        p = B[0];q = B[1]
        for j in range(len(X)):
            X[j] = p*X[j]
        X.append(q)
        g = math.gcd(g,A[i])
    return X


print(bezout(111,30))
print(bezoutN([111,30,7]))
print(bezoutN([111,30,7,11]))

出力

[3, -11]
[-6, 22, 1]
[-6, 22, 1, 0]

いい具合ですね。

bezoutNの時間計算量は $O (N l o g (m a x (A)) + N^{2})$ です。
ところで、このコードにはいくつか改善できる点があります。

時間計算量改善

$O (N l o g (m a x (A)) + N^{2})$ というと、パット見 $N^{2}$ がネックになってそうです。
これはベズー係数を保存しておいて、掛け算を後でまとめてやるだけでOKです。
変更後のオーダーは $O (N l o g (m a x (A)))$ です。

ソースコード

import math

def bezout(a,b):
    if b==0:
        return [1,0]
    r = a%b
    q = (a-r)//b
    
    d = bezout(b,r)
    D = [d[1],d[0]-q*d[1]]
    return D
    
def bezoutN(A):
    if len(A)<=0:
        return []
    g = A[0]
    P = [];Q=[]
    for i in range(len(A)):
        if i==0:
            continue
        B = bezout(g,A[i])
        p = B[0];q = B[1]
        P.append(p)
        Q.append(q)
        g = math.gcd(g,A[i])
    
    X = [0]*(len(A))
    now = 1
    for i in reversed(range(len(A)-1)):
        X[i+1]=now*Q[i]
        now = now*P[i]
    X[0]=now
    return X


print(bezout(111,30))
print(bezoutN([111,30,7]))
print(bezoutN([111,30,7,11]))

出力

[3, -11]
[-6, 22, 1]
[-6, 22, 1, 0]

オーバーフロー対策その1

この計算だと、 $N$ 項のうち前の方、とくに初項は $N - 1$ 個のベズー係数がかかっています。
オーバーフローを心配したくなりますよね。
そこで、前の係数をできるだけ小さくしたいです。

ここでベズーの等式の性質を使います。
$a x + b y = g$ として、

∣ x ∣ < = ∣ ∣ ∣ ∣ ∣ \frac{b}{g} ∣ ∣ ∣ ∣ ∣, ∣ y ∣ < = ∣ ∣ ∣ ∣ ∣ \frac{a}{g} ∣ ∣ ∣ ∣ ∣

をみたす $(x, y)$ を拡張ユークリッドの互除法が与えてくれるということは先述しました。
なので、 $∣ x ∣$ が最小であるようなベズー係数は拡張ユークリッドの互除法がもたらしたものを $(x, y)$ として、

(x, y), (x + \frac{b}{g}, y - \frac{a}{g}), (x - \frac{b}{g}, y + \frac{a}{g})

のどこかにあるということになります。
$∣ x ∣$ が最小なベズー係数を見つけてあげれば、オーバーフローを起こしにくくなります。(気休め程度な気もするが・・・)

オーバーフロー対策その2

気休め程度が気に食わないので、オーダーレベルで対策をします。

a_{1} x_{1} + . . . + a_{n} x_{n} = g_{1}

b_{1} y_{1} + . . . + b_{m} y_{m} = g_{2}

g_{1} p + g_{2} q = g c d (g_{1}, g_{2})

を合体すると、

a_{1} p x_{1} + . . . + a_{n} p x_{n} + b_{1} q y_{1} + . . . + b_{m} q y_{m} = g c d (g_{1}, g_{2})

を得ます。

つまり、 $(a_{1}, . . ., a_{n})$ のベズー係数 $(x_{1}, . . ., x_{n})$ と $(b_{1}, . . ., b_{m})$ のベズー係数 $(y_{1}, . . ., y_{m})$ がわかっていれば、

$(g c d (a), g c d (b))$ のベズー係数 $(p, q)$ を拡張ユークリッドの互除法を用いて一つ求める。
$(p x_{1}, . . ., p x_{n}, q y_{1}, . . ., q y_{1})$ が $(a_{1}, . . ., a_{n}, b_{1}, . . ., b_{m})$ のベズー係数の一つである。

という手順で $(a_{1}, . . ., a_{n}, b_{1}, . . ., b_{m})$ のベズー係数が $O (n + m + l o g (m a x (a, b))$ で計算できます。
では $(x_{1}, . . ., x_{n})$ と $(y_{1}, . . ., y_{m})$ をどうやって計算するかというと、再帰を使います。
セグ木やFFTと同じですね。単項になったらそのベズー係数は $1$ でしょう。

これをうまく使うことで $O (N (l o g (m a x (A)) + l o g N))$ でN項のベズー係数を計算できます。logが一つ余計につきましたが、加算なのでそれもあまり気になりません。それに、各項にかかるベズー係数の個数が $O (l o g N)$ 個になってます！これはかなりオーバーフロー対策と言えるのではないでしょうか？
~~実は $1 0^{9}$ レベルの係数を与えられると2,3発でアウトなのだが･･･~~

ソースコード

import math

def bezout(a,b):
    if b==0:
        return [1,0]
    r = a%b
    q = (a-r)//b
    
    d = bezout(b,r)
    D = [d[1],d[0]-q*d[1]]
    return D
    
def bezoutN(A):
    if len(A)<=0:
        return []
    if len(A)==1:
        return [1]
    A1 = A[:(len(A)//2)]
    A2 = A[(len(A)//2):]
    
    #実はここのgcdを可読性のために愚直計算にしている影響で計算量が
    #O(Nlog(max(A))+NlogN^2)になり、logが一つ増えます
    #bezoutNがgcdを同時に返すことでこれは解消します
    g1 = A1[0]
    for i in range(len(A1)):
        g1 = math.gcd(g1,A1[i])
    g2 = A2[0]
    for i in range(len(A2)):
        g2 = math.gcd(g2,A2[i])
    
    B = bezout(g1,g2)
    p = B[0];q=B[1]
    x = bezoutN(A1)
    y = bezoutN(A2)
    
    X = [0]*(len(A))
    for i in range(len(x)):
        X[i] = x[i]*p
    for i in range(len(y)):
        X[len(A1)+i] = y[i]*q
    
    return X


print(bezout(111,30))
print(bezoutN([111,30,7]))
print(bezoutN([111,30,7,11]))

出力

[3, -11]
[0, -3, 13]
[0, 0, -3, 2]

出力されているベズー係数が変わりましたね！
2項のときに一意でないと言ったように、N項でもベズー係数は一意ではありません。ですが $111 \times 0 + 30 \times - 3 + 7 \times 13 = 1$ 、 $111 \times 0 + 30 \times 0 + 7 \times - 3 + 11 \times 2 = 1$ からわかる通り、ベズー係数としての定義は満たしています！

おまけ:中国剰余定理

競技プログラマーの間では単に中国剰余定理あるいはCRTと呼ばれるテクニックである、
互いに素な整数 $m, n$ と整数 $a, b (0 < = a < n, 0 < = b < m)$ があり、

x \equiv a (m o d m), x \equiv b (m o d n)

であるとき

x \equiv c (m o d m n)

を満たす整数 $c (0 < = c < m n)$ を求める。
というアルゴリズムは、拡張ユークリッドの互除法を用いて実行できます！

$(m, n)$ のベズー係数 $(u, v)$ を拡張ユークリッドの互除法を用いて一つ求める
$c = a n v + b m u$ (を $m n$ で割ったあまり)である。

あとがき

最初はextGCDを自作ライブラリに追加するために拡張ユークリッドの互除法の勉強を始めたんですよ。

extGCD持ってなくて必要になった時いつもけんちょんのブログからパクってたんだけどとうとう自前のextGCDが完成した
— ⚡すく⚡ (@0214sh7) April 7, 2021

それで次はCRTの勉強･ライブラリ化に行くのかと思いきやライブラリページの命名に悩んだ結果ベズー係数の存在を知り、気づけばベズー係数すきすき侍と化していました。
数学科に入った結果代数への解像度が上がったせいです　数学科ってこわいね
このブログも代数の教科書を見ながら書いています。

そしてN項のベズー係数を求める方法を探した結果日本語の記事が見つからなかった(英語はあった)ので、この記事を作成しました。
N項のベズー係数を求める方法を知りたい人に届くことを祈っています。

参考文献

Harold M. Stark, An Introduction to Number Theory,MIT press,The MIT Press,1978.(芹沢正三,安藤四郎訳『初等整数論』,現代数学社).

中島匠一,『代数と数論の基礎』,共立出版,2000.

ベズーの等式,Wikipedia,2020年11月18日更新,2021年4月14日アクセス.
https://ja.wikipedia.org/wiki/ベズーの等式

Extended Euclidean algorithm,Wikipedia,2021年1月29日更新,2021年4月14日アクセス.
https://en.wikipedia.org/wiki/Extended_Euclidean_algorithm

けんちょん (Otsuki),拡張ユークリッドの互除法〜一次不定方程式 ax + by = c の解き方〜,Qiita,2019年10月17日更新,2021年4月14日アクセス.
https://qiita.com/drken/items/b97ff231e43bce50199a

ベズー係数とN項の拡張ユークリッドの互除法

拡張ユークリッドの互除法とは？

ベズー係数

3項でのベズー係数

N項でのベズー係数

時間計算量改善

オーバーフロー対策その1

オーバーフロー対策その2

おまけ:中国剰余定理

あとがき

参考文献

この記事をシェア

関連する記事