4次元を覗く

お詫び

この前にUntitledの記事が投稿されてしまいました。お騒がせしました。これが出す予定だった記事です。

どゆこと

僕は3DCGに興味があって、いろいろなことをやっています。例えば以下のようにですね。

どうでもいいけどこの記事1年前なんすね。はやい。

そんで、この前WebGLのライブラリみたいなの(Three.js的な)を作ったんですけど、普通に3DCGするのに飽きてしまったんですね。

それで、前からやろうと思っていた4次元のレンダリングをしようと思い立ったわけです。

4次元ってどんなの

要は3次元(x, y, z)に次元を一つ足したもの(x, y, z, w)です。今回はWikipedia内にある4次元立方体の回転を見るところまでやります。

そもそも3次元のレンダリングはどうやっているか

今回利用するのは割と簡単に複雑な図形が描画できるレイマーチングという方式を利用します。その方式について、詳しくは僕の過去記事(さっき上げた奴)を参照してください。

普通我々は様々なものに当たって反射した光が目に入ることで世界を知覚するわけですが、目に入ってくる光を何か物体に当たるまで逆算しようというのがレイトレーシングやレイマーチングの考え方なわけです。逆算するときに考える仮想的な光の軌跡を「レイ」と呼び、光の軌跡を逆算することを「レイを飛ばす」と表現します。今回は簡単のため、反射や屈折は考えないことにします。

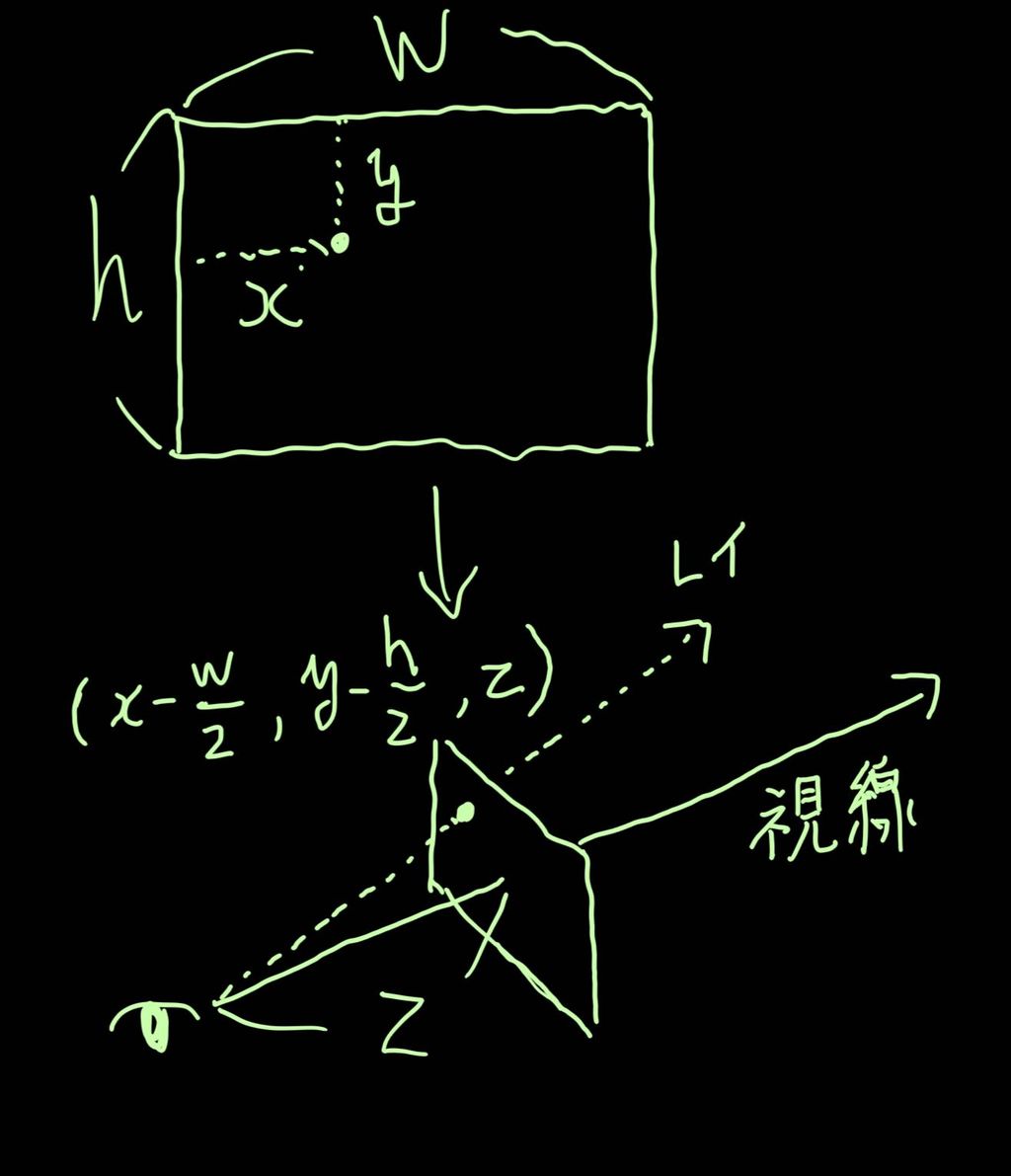
さて、レイの飛ばす方向はどうすればよいのでしょうか。これは簡単な話で、レイの出発点を原点とし、視線をz+方向に向けたとすると、例えば出力画像(サイズは(W, H)とする)の座標(x, y)の色を求めたかったら、z先の(x - 0.5W, y - 0.5H, z)を通るような方向にレイを飛ばせばよいのです。これは風景画を描く人が手で四角形の枠を作ってその中から覗くようなものです。レイの出発点や視線方向を変えようと思ったらそれを平行移動や回転移動すればよいだけです。私たちが実際に世界を見るときはもっと幅広い方向から光が入ってきますが、CGの世界ではこれでよいのです。

4次元のレンダリング

3次元と大きく考え方が変わるわけではありません。3次元との違いは次元が増えたことだけです。ちなみに出力も2次元から3次元になります。

先ほどと同じように考えます。レイの出発点を原点とし、視線をw+方向に向けたとすると3次元画像(?)(W, H, D)上の点(x, y, z)の色を求めるためにw先の(x - 0.5W, y - 0.5H, z - 0.5D, w)の点を通るような方向にレイを飛ばします。

また、4次元立方体の距離関数も用意しなくてはいけません(距離関数に関しては過去記事参照)。3次元立方体(各辺の長さ1)の距離関数は

float box(vec3 pos) {
    vec3 q = abs(pos) - 1.0;
    return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
}

なので、4次元立方体の距離関数は

float box4d(vec4 pos) {
    vec4 q = abs(pos) - 1.0;
    return length(max(q,0.0)) + min(max(q.x,max(q.y,max(q.z, q.w))),0.0);
}

となります。これで、4次元立方体は描画できますね。

と言いたいところですが、まだ問題はあります。このままでは3次元に投影されているのです。私たちが普段見てる画面は2次元ですから、次元を落としてやらねばなりません。

そこでどうするか、答えは「もう一度レイトレーシング」です。いま4次元が3次元に投影されているので、普段3次元を2次元に落とし込んでいるようにやればよいのです。ただし、距離関数は無いのでレイマーチングができません。そのためレイを進める距離を一定にして、レイを進めるたびに4次元方向にレイマーチング、何にもぶつからなかったらレイトレーシング続行、というようにやります。ここの負荷が結構でかいです。

回転

4次元での回転はどのように扱えばよいのでしょうか。それを考えるために2次元、3次元での回転を考えてみます。

ある点を原点中心に回転させる場合、２次元の回転では、原点を中心として回転させる、というのは直観的にわかると思います。同様に3次元の回転ではx, y, z軸を軸として回転させます。この時、ある点の座標は二つだけが変換され、その他は変化しない、という性質があります。例えば(0, 0, 1)の点をθ回転させると、(0, sinθ, cosθ)となり、x成分は変化しません。このことを考えると4次元での回転は平面を固定する、という考えになります。４つの次元から固定する成分2つの選び方は6通りあるので、回転平面も6つあることになります。これが4次元での回転です。

今回は冒頭でも述べた回転を再現するため、y,z成分を固定するように回転させました。

ライティング

CGではライティングも重要です。物体が光に当たっているように見せる処理です。今回は簡単にlambert法でライティングします。lambert法では物体の法線を求める必要があります。

vec3 calcNorm(vec3 pos)
{
    vec2 d = vec2(0.0001, 0.0);
    vec3 grad = vec3(
        map(pos+d.xyy)-map(pos-d.xyy),
        map(pos+d.yxy)-map(pos-d.yxy),
        map(pos+d.yyx)-map(pos-d.yyx)
    );
    return normalize(grad);
}

これが3次元での法線の求め方です。距離関数のx, y, z方向の微分を取ったものですね。まぁ当然4次元では

vec4 calcNorm4d(vec4 pos)
{
    vec2 d = vec2(0.0001, 0.0);
    vec4 grad = vec4(
        map4(pos+d.xyyy)-map4(pos-d.xyyy),
        map4(pos+d.yxyy)-map4(pos-d.yxyy),
        map4(pos+d.yyxy)-map4(pos-d.yyxy),
        map4(pos+d.yyyx)-map4(pos-d.yyyx)
    );
    return normalize(grad);
}

となりますね。lambertは簡単で、ライト方向と法線方向の内積を取るだけです。

float lighting4d(vec4 pos)
{
    return saturate(dot(calcNorm4d(pos), -LIGHT_VECTOR));
}

できた

上で述べたことをいろいろやると4次元立方体の回転を見ることができます。デモは以下。(重めなのでお気を付けください。参考程度にいうとRadeon Graphics(CPU内臓)で35fpsぐらいでした)

マウスでいろいろな角度から見れると思います。

(縞模様が見えるかもしれませんがそれはレンダリングの過程で生じるものです。どうしても消せなかった...)

まとめ

4次元での投影楽しいですね。暇があったらラスタライズ法でも4次元できるようにしたさはあります。あと最近は非ユークリッド幾何の投影も気になっているのでやるかもしれません。

明日はNABE君の線画交換会の話らしいです。お楽しみに。