新歓ブログリレー2020 50日目の記事です

Heap とは、全順序集合の多重部分集合に対して挿入や最小値の取得、削除が可能なデータ構造です。C++ では std::priority_queue が該当します。

特に Meldable Heap は meld、すなわち 2 つの Heap を融合させて 1 つの Heap にする操作を提供する Heap を指します。Meldable Heap には様々なバリエーションが存在し、本稿ではその 1 つである Randomized Meldable Heap と呼ばれるデータ構造を紹介します。

構造

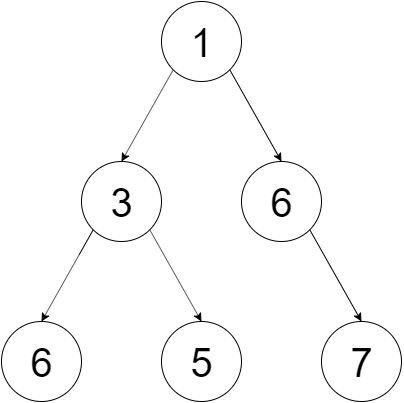
全てのノードが丁度 1 つの要素と対応する、自由な形の二分木を管理します。

この二分木は heap property を維持します。すなわち全てのノードのついて、その要素は子ノードの要素以下になるようにします。この条件が満たされるとき、根には常に最小の要素が対応することが分かります。

meld

2 つの二分木 x, y を、heap property を維持したまま 1 つの木に統合します。それぞれの木の根を比較し、一般性を失わず x の方が小さかったとします。x の根が統合された木の根となり、x の子のうち一方を等確率でランダムに選び、それと y を meld したものを新しい子とします。x, y のいずれか一方が空になったときもう一方が meld 結果となり、再帰が終了します。

このアルゴリズムが heap property を維持することを確認します。仮定より y は x 以上であり、したがって y の全てのノードは x 以上です。よって子と meld した後もその根は x 以上となるので成立します。

最も興味深いのは、このアルゴリズムの時間計算量が木の形状に関わらず O(log|x|+log|y|) となることです。1 以上の定数 c が存在して、時間計算量が  c(log(|x|+1)+log(|y|+1)) 以下となることを数学的帰納法を用いて証明します。

|x|=0 の場合、直ちにアルゴリズムが終了することから条件は満たされます。

|x|≠0 のとき、x の左の子を l、右の子を r とすると、以下のようになります。

$1+\frac{1}{2}c(\log (|l|+1)+\log (|y|+1))+\frac{1}{2}c(\log (|r|+1)+\log (|y|+1))$
$=\frac{1}{2}c\log ((|l|+1)(|r|+1))+1+c\log (|y|+1)$
$\le \frac{1}{2}c\log ((\frac{|x|+1}{2}{)}^2)+1+c\log (|y|+1)$
$=c(\log (|x|+1)-1)+1+c\log (|y|+1)$
$\le c(\log (|x|+1)+\log (|y|+1))$

insert

単一のノードからなる木を作成し、meld します。

pop

根を削除し、左右の子を meld します。

その他

Meldable Heap には他に Leftist Heap、Skew Heap、Pairing Heap、Fibonacci Heap など多種存在します。どのアルゴリズムも面白く、おすすめです。

明日の担当者は @bonc256 です。