新歓ブログリレー2020 38日目の記事です。
競技プログラミングに役に立つかもしれないアルゴリズムのSuffix Array Induced Sorting(SA-IS)を構築する話をします。
@idatenに触発されて書きました(やったぁ)
SA-ISってなに
SA-ISとは高速でSuffix Array(接尾辞配列)構築するアルゴリズムです。
Suffix Arrayを作ると何がうれしいかと言うと、高速に全文検索ができるようになります。
また、SA-ISは Suffix Array Induced Sortingのそれぞれの頭文字をとったものからきているようです。
バイオインフォマティクスのDNAシーケンスの検索のときに使われるとか使われないとか… よくわからないんですけど。
接尾辞ってなに
接尾辞と言われてもよくわからないので説明します。
ある文字列の部分文字列の終端を同じくして、始点の異なるもののことです。
よくわからないので実例で表すと、TOUKOUDAIの接尾辞は、短い順に、I、AI、DAI、UDAI、OUDAI、KOUDAI、UKOUDAI、OUKOUDAI、TOUKOUDAIの9つがそうです。
つまり、今回の例ではすべて最後がIで終わっていることがわかります。
(要は末尾が固定されているため)。そのような文字列を接尾辞といいます。
接尾辞配列ってなに
接尾辞が配列になったものです(超ざっくり)
文字列TOUKOUDAIの接尾辞すべてがまとまったもので、これを辞書順(あいうえお順とか、ABC順とか言われるやつ)に並び替えます。それをそれぞれの接尾辞が何番目の文字から始まっているかを記録したものです。
言ってもよくわからないので、実例で説明すると、
TOUKOUDAIから得られるすべての接尾辞配列は以下の9つ。
[I、AI、DAI、UDAI、OUDAI、KOUDAI、UKOUDAI、OUKOUDAI、TOUKOUDAI]
これを辞書順に並べる(辞書順は "a" < "aa" 、"a" < "b" のような順序決め)。
[AI、DAI、I、KOUDAI、OUDAI、OUKOUDAI、TOUKOUDAI、UDAI、UKOUDAI]
それぞれの文字列の先頭部分が元の文字列のどこから始まっているかを見ます。
つまり、TOUKOUDAIなら最初から始まっています。
KOUDAI なら最初から3番目より始まっています(0始まりで数える)。
TOUKOUDAIは0番目。KOUDAIは3番目ということになります。
整理すると、[ 7 , 6 , 8 , 3 , 4 , 1 , 0 , 5 , 2 ] となります。
この[ 7 , 6 , 8 , 3 , 4 , 1 , 0 , 5 , 2 ]こそが今回このAdCで頑張って求める接尾辞配列です。
普通に接尾辞配列を求める
とりあえず辞書順が欲しいのでソートしようという考えは至極自然ですね。
なので、ソートして求めます(雑な実装例がこちら)
import java.util.ArrayList;
import java.util.Comparator;
import java.util.Scanner;
class SuffixArray{
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
String source=sc.next(); //入力
ArrayList<Pair> input=new ArrayList<Pair>();
ArrayList<Integer> sufary=new ArrayList<Integer>(source.length());
for(int i=0; i<source.length(); i++) {
String tmpstr=source.substring(i);
input.add(new Pair(tmpstr,i));
}
input.sort(Comparator.comparing(p -> p.suffix)); //辞書順でソート
for(int i=0; i<input.size(); i++) {
sufary.add(input.get(i).index);
}
System.out.println(sufary);
sc.close();
}
static class Pair{
String suffix;
int index;
Pair(String s,int i){
suffix=s;
index=i;
}
}
}
どこから始まっているか(index)と文字列(Suffix)を構造体として持っておき、その構造体を文字列の辞書順でソートしたときのindexの順番がSuffix Arrayとなります。
おそらく、同じような手法でもっとうまいやり方はあると思いますがわからないです…
ソートで求める接尾辞配列の問題点
- 部分文字列をすべて持っているため、元の文字列の長さをとすると、の記憶領域が必要になる
- うまいことやると部分文字列を持たなくてもいいですが、そこまで重要ではないので省略します。
- ソート時間がかかる。具体的にはかかる。
(文字列同士の比較にかかるため全体でとなります)
SA-ISの紹介と解説
ソートで求める方法ではメモリも時間もたりなくなってしまう…そうならないように高速で求めるためにSA-ISを使います。
これからSA-ISについて解説しまするので大雑把な流れをここで把握しておきましょう。
- 流れ1 SA-ISのために行う下処理で文字を2類に分ける(S型、L型とS型をさらに分けたLMS)
- 流れ2 3つに分けた文字を種類ごとに決められた手順で配列に入れる
- 流れ3 それでもうまくいかないときは…?
ざっくりとこんな感じです。これを繰り返すとできます。
ここで出てきたよくわからない用語は順を追って説明します。
この記事を読む時間がない人は記事の下のところに実装例を載せておくので参考にしてみてください。
仕掛け1. L型とS型
これ以降、接尾辞配列を作る文字列を文字列とします。また、数の数え方を0始まり(0-indexed)とします。
まず、文字列の末尾にどの文字よりも辞書順で先に来る仮の文字を付加します。
(TOUKOUDAIに仮の文字*を付け足して、TOUKOUDAI*とする)。
末尾に最も優先度の高い文字を付け足すことで後の処理が楽になります。
の末尾に文字を付加した文字列をとします。
例)
ここで、LとSについて説明します。
文字列の文字目と文字目について見る。
文字目は型というのは、文字目が文字目よりも辞書順で先の場合(例: abのa)。
文字目は型というのは、文字目が文字目よりも辞書順で後の場合(例: baのb)。
また、文字目と文字目が同じだった場合、文字目の型と同じになります。
ちなみに末尾の文字は型です(次の文字がないのでそういう決まりです)。
また、この処理は文字列を末尾から見ていきます。
例えば、TOUKOUDAI*だとこうなります。
| T | O | U | K | O | U | D | A | I | * |
|---|---|---|---|---|---|---|---|---|---|
| L | S | L | S | S | L | L | S | L | S |
OOOKAYAMA*は以下の通り。
| O | O | O | K | A | Y | A | M | A | * |
|---|---|---|---|---|---|---|---|---|---|
| L | L | L | L | S | L | S | L | L | S |
最初のOの連続は、文字目のKが型であることからすべて型となります。
仕掛け2. LMS(最左のS)
仕掛け1で文字列をLとSに分けました。次に目印となるLMSを探します。
LMSとは、文字目が型で、文字目が型となる所のことで、「番目がLMS」のように言います。
TOUKOUDAI*。
| T | O | U | K | O | U | D | A | I | * |
|---|---|---|---|---|---|---|---|---|---|
| L | S | L | S | S | L | L | S | L | S |
| LMS | LMS | LMS | LMS |
O、K、A、*がLMSとなります。
また、OOOKAYAMA*は以下の通り。
| O | O | O | K | A | Y | A | M | A | * |
|---|---|---|---|---|---|---|---|---|---|
| L | L | L | L | S | L | S | L | L | S |
| LMS | LMS | LMS |
となります。
文字目と文字目がLMSであり、となる文字目がLMSで無いとき、文字目から文字目の部分文字列をLMS部分文字列と言います。また、例外的に最後の*のみもLMS部分文字列とします。
例えば、TOUKOUDAI*であれば、OUK、KOUDA、AI*、*の4つ。
OOOKAYAMA*ならば、AYA、AMA*、*の3つが該当します。
このLMS部分文字列は、少なくとも1文字以上で構成されているという性質をもつ(*も含めた場合。除くと最低3文字)。
なぜ最低3文字なのかというと、LMSで囲まれているため両端の文字は型が来ます。また、LMSとなる条件は型の文字の1つ前に型が来ることです(そういう定義)。そのため、最短でもという構成になるため3文字以上です。
ざっくりいうと、LMS部分文字列というのは、先頭の1文字と末尾の1文字がどちらもLMSで構成されていて、それ以外にLMSを持たない文字列。例外的に最後の末尾文字のみもLMS部分文字列とすることがある。 ということです。
ステップ1 LMS部分文字列を入れる
まず、LMS部分文字列を登場が遅い順に、先頭の文字でソートします。
ここでのソートは使われる文字が限定されているので(アルファベットのみ等)、バケットソートを使うことで高速にソートができます。
TOUKOUDAI*は登場が遅い順に、*、AI*、KOUDA、OUKとなります。これを先頭の文字のみでソートします。
登場が遅い順で末尾に入れていきます(つまり、登場の早い順に配列の後ろから前に入れる事と同じになります)。
*:["*"]
A:["AI*"]
B:[]
C:[]
︙
K:["KOUDA"]
︙
O:["OUK"]
OOOKAYAMA*の場合は、*、AMA*、AYAの3つ。
*:["*"]
A:["AMA*" , "AYA"]
これだけ見ると、AMA*とAYAがきちんと辞書順にならんでいるのでちょっとできすぎなケースです。
では、OOOKAMAYA*ではどうでしょうか。
| O | O | O | K | A | M | A | Y | A | * |
|---|---|---|---|---|---|---|---|---|---|
| L | L | L | L | S | L | S | L | L | S |
| LMS | LMS | LMS |
なので、LMS部分文字列は、AMA、AYA*、*の3つ。
登場遅い順に並べると、*、AYA*、AMAです。
これを先頭の文字列でバケットソートを行う。
*:["*"]
A:["AYA*" , "AMA"]
辞書順ではAMA、AYA*なので少し不自然ですが、いまやりたいのは辞書順でソートすることではなく、登場が遅い順に並べることです。そして、それを先頭の文字でバケットソートを行っているだけです。なので、必ずしも辞書順に並ぶとは限りません。
ステップ2 型文字を並べる
本番その1でLMS部分文字列をバケットソートしました。
TOUKOUDAI*は以下の通り。
*:["*"]
A:["AI*"]
K:["KOUDA"]
O:["OUK"]
接尾辞の開始インデックスは以下の通り(これ以降説明のためにインデックスで説明をします)。
*:[ 9 ]
A:[ 7 ]
K:[ 3 ]
O:[ 1 ]
の4つがすでに入っている状態になります。
その2では、先頭から配列を走査してL型の接尾辞を入れます。
具体的には、配列に入っている要素の1つ前の文字がL型ならその文字の配列の末尾に値を追加する。S型であったり、該当する文字がない場合は追加しない。
末尾に追加し続けるということは、配列の添え字が小さいほうから大きいほうに値を入れることと同じになります。
| T | O | U | K | O | U | D | A | I | * |
|---|---|---|---|---|---|---|---|---|---|
| L | S | L | S | S | L | L | S | L | S |
| LMS | LMS | LMS | LMS |
*:[ 9 <- いまここ ]
A:[ 7 ]
K:[ 3 ]
O:[ 1 ]
ちなみにで説明しています。
9番目の1つ前の(=8)番目文字であるIは型なので、Iの配列に8を入れる。
*:[ 9 <- いまここ ]
A:[ 7 ]
I:[ 8 <- 新しく追加した ]
K:[ 3 ]
O:[ 1 ]
つぎに、Aの配列に入っている値を見る。
*:[ 9 ]
A:[ 7 <- いまここ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
7番目の1つ前の6番目の文字のDは型なのでDの配列に入れる。
*:[ 9 ]
A:[ 7 <- いまここ]
D:[ 6 <- 新しく追加した ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
Aの配列を見終わったので次はDの配列を見る。
*:[ 9 ]
A:[ 7 ]
D:[ 6 <- いまここ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
次にDの配列に入っている6番目の1つ前の5番目の文字Uも型なので、追加する。
*:[ 9 ]
A:[ 7 ]
D:[ 6 <- いまここ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
U:[ 5 <- 新しく追加した]
つぎにIの配列を見る。 8番目の1つ前の7番目の要素はすでに入っているのでスキップ。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 <- いまここ]
O:[ 1 ]
U:[ 5 ]
次のK配列に入っている3番目の1つ前の2番目のUも型なのでUの配列の末尾に入れる。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 <- いまここ]
O:[ 1 ]
U:[ 5 , 2 <-新しく追加した ]
見るのはOの配列。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 <- いまここ]
U:[ 5 , 2 ]
つぎにOの配列に入っている1の1つ前の0番目のTは型なのでTの配列に入れる。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 <- いまここ]
T:[ 0 <- 新しく追加した]
U:[ 5 , 2 ]
次に見るのは、Tの配列。0番目よりも前にある要素はないのでスキップ。
つぎは、Uの配列の先頭。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
T:[ 0 ]
U:[ 5 <- いまここ, 2 ]
4番目の要素のOは型なのでスキップ。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
T:[ 0 ]
U:[ 5 , 2 <- いまここ]
次は、2。2の1つ前はすでに埋まっているのでスキップ。これですべて見たので本番2は終了。
おわかりいただけただろうか 本番2のすごいところに
おわかりいただけただろうか…
お分かりいただきたいところは、新しく追加したものはすべて今見ているものよりも必ず後に来ていることを。
これはなぜなのか。
値は今見ている文字の型にかかわらず、その1つ前の文字の型が型の場合に追加される。
つまり、「今見ている文字は型で1つ前は型の時」または、「今見ている文字は型且つ1つ前も型」の時値が追加されます。
まず、「今見ている文字は型で1つ前は型の時」を考える。
追加する文字は型なので、今見ている文字型よりも辞書順が後にあるため、当然今見ているところよりも後の配列に値が追加されます。
次に、「今見ている文字は型で、1つ前も型」の時を考える。
どちらも型かつ、どちらも同じ文字であるとき。それは見ている文字の配列の末尾に値が追加されるので今見ている文字よりも後に追加されます。
どちらも型で、お互い文字が異なる場合。これは型の性質より、今見ている文字よりも、1つ前の文字のほうが辞書順で後なのでこれも同様に今見ている文字がある配列よりも後の配列に値が追加されます。
以上から追加する文字は今見ている文字よりも必ず後に追加される事がわかります。
ちょっと文字がごちゃごちゃしていて分かりづらいので図で説明すると以下の通り
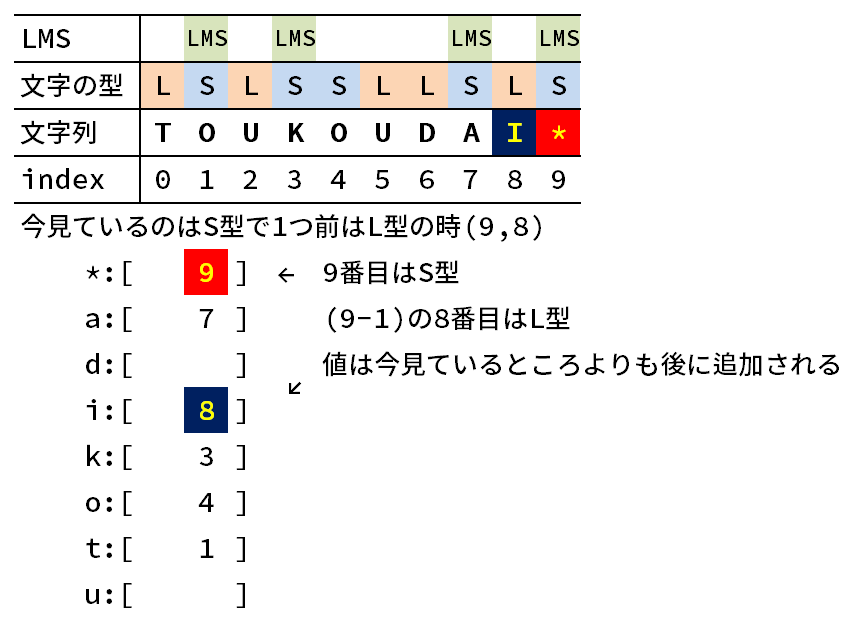
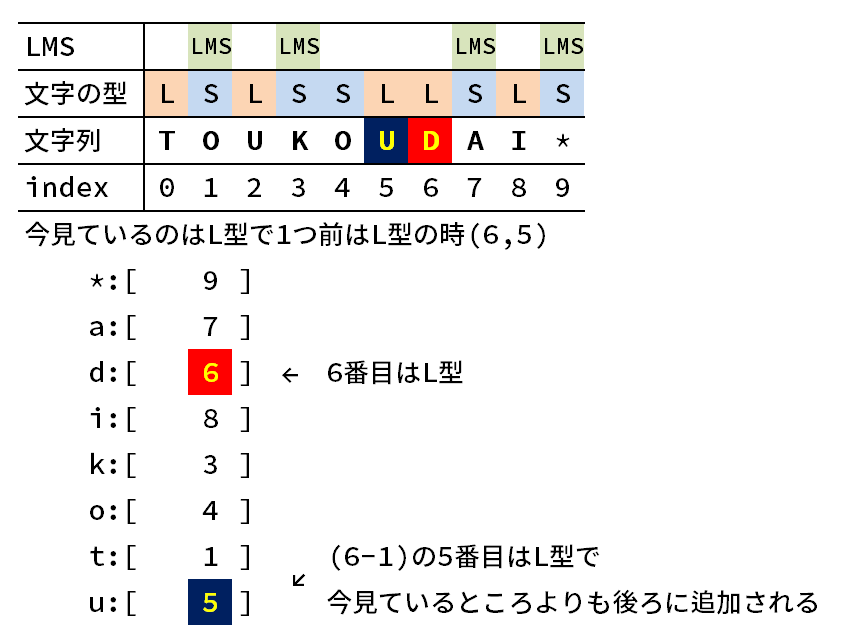
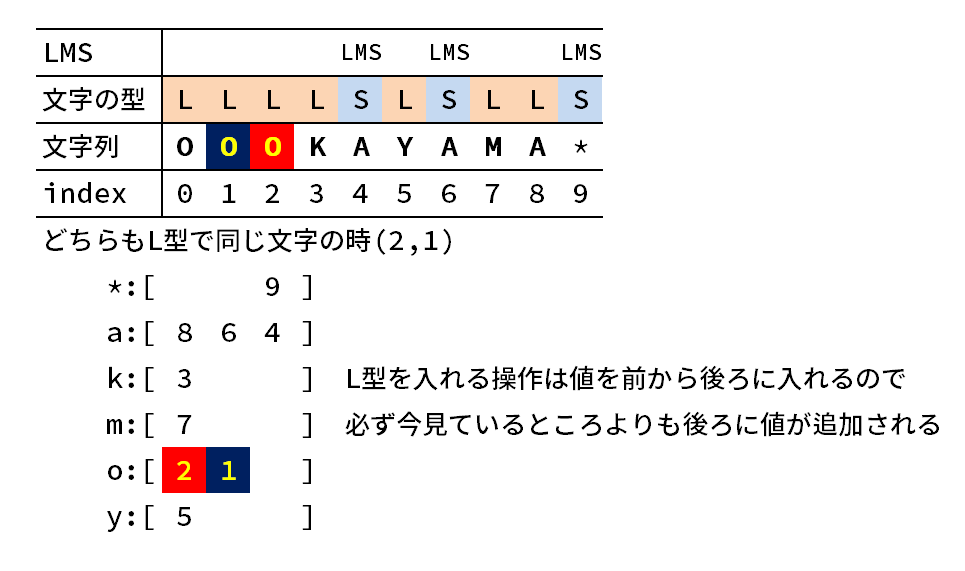
ステップ3 LMS部分文字列を取り除く
ステップ1で割と適当にLMS部分文字列を入れたので、取り除きます。
(ステップ1を確認。必ずしもLMSのindexが辞書順に並ぶわけではないので、このまま残しておくと最後に出来上がるSuffix Arrayへ影響を与えかねない)。
*:[ 9 ]
A:[ 7 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 ]
O:[ 1 ]
T:[ 0 ]
U:[ 5 , 2 ]
これから最後のLMSのインデックスのを除いた1,3,7を取り除く(9番目よりも後にあるものがなく、後から追加できない為)
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
T:[ 0 ]
U:[ 5 , 2 ]
ステップ4 型文字を入れる
LMSの条件に見合う文字は必ず型で、その次に型文字を入れました。そして、LMSを削除したのでLMSを含む型文字を入れる必要があるので入れます。
今度は、本番2と逆の方針で入れていきます。
つまり、後ろから見ていき、値を前に追加します。
値を配列の添え字が大きいほうから小さいほうに入れることと同じです。
| T | O | U | K | O | U | D | A | I | * |
|---|---|---|---|---|---|---|---|---|---|
| L | S | L | S | S | L | L | S | L | S |
| LMS | LMS | LMS | LMS |
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
T:[ 0 ]
U:[ 5 , 2 <- いまここ]
今見ている2のインデックスの1つ前の1番目の文字は、Oで型なので配列の先頭に入れる。
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
O:[ 1 <- 新しく追加した]
T:[ 0 ]
U:[ 5 , 2 <- いまここ]
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
O:[ 1 ]
T:[ 0 ]
U:[ 5 <- いまここ , 2 ]
次に5の1つ前の4番目Oは型なので追加する。
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
O:[ 4 <- 新しく追加した , 1 ]
T:[ 0 ]
U:[ 5 <- いまここ , 2 ]
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
O:[ 4 <- いまここ, 1 ]
T:[ 0 ]
U:[ 5 , 2 ]
つぎの0は1つ前が存在しないのでスキップ。次の1のその前はすでに埋まっているのでスキップ。
次に4の1つ前の3は型なので入れる。
*:[ 9 ]
D:[ 6 ]
I:[ 8 ]
K:[ 3 <-新しく追加した ]
O:[ 4 <- いまここ, 1 ]
T:[ 0 ]
U:[ 5 , 2 ]
*:[ 9 ]
D:[ 6 ]
I:[ 8 <-いまここ]
K:[ 3 ]
O:[ 4 , 1 ]
T:[ 0 ]
U:[ 5 , 2 ]
3の1つ前の2は埋まっているのでスキップ。次の8-1の7番目のAは型なので入れる。
*:[ 9 ]
A:[ 7 <-新しく追加した]
D:[ 6 ]
I:[ 8 <-いまここ]
K:[ 3 ]
O:[ 4 , 1 ]
T:[ 0 ]
U:[ 5 , 2 ]
次に6,7,9を見ていく。それぞれ5,6,8番目はすでに埋まっているのでスキップ。これによって最後まで見たので終了。
これによって、いつの間にかLMS、そうでない型までも追加されました。
そしてこれによってLMS部分文字列に重複のない場合はこれでLMS部分文字列のところも問題なく辞書順に並びました。
ステップ5 重複するLMS部分文字列と辞書順
今回の例のTOUKOUDAI*、OOOKAYAMA*、OOOKAMAYA*はいずれもLMS部分文字列はすべて異なったため本番3までできちんと求まりました。しかし、それでは求まらないケースというものが存在します。
それはどのようなケースでしょうか。
それは、繰り返しがある文字列や、それが部分的にあるものです(ざっくりと言うと)。
| z | a | z | a | z | a | z | a | z | * |
|---|---|---|---|---|---|---|---|---|---|
| LMS | LMS | LMS | LMS | LMS |
例えば、zazazazaz*とかです。zazazazaz*のLMSはaと*にあります。
つまりLMS部分文字列は、aza、aza、aza、az*、*の3種類しかありません(azaが3つある)。
つまり、LMS部分文字列だけでは区別できないものが存在し、このままでは正しい辞書順が作れないということです。
では、区別できないLMS部分文字列が存在したとき、今までに操作して作った配列は無駄だったのでしょうか。
結果としてはノーで、LMS部分文字列の後の文字列も含めたときの辞書順に並んでなくとも、LMS部分文字列のみに着目すると全体として辞書順にならんでいることがわかります。
例えば、TOUKOUDAI*とzazazazaz*において今まで紹介した操作を行ったときの接尾辞配列はそれぞれこうなっています。
例1 TOUKOUDAI*
| index | 接尾辞 |
|---|---|
| 9 | * |
| 7 | AI* |
| 6 | DAI* |
| 8 | I* |
| 3 | KOUDAI* |
| 4 | OUDAI* |
| 1 | OUKOUDAI* |
| 0 | TOUKOUDAI* |
| 5 | UDAI* |
| 2 | UKOUDAI* |
この例はLMS部分文字列に重複がないのでこの時点ですべての接尾辞が辞書順に並んでおりSuffix Arrayが完成しています。
実際、最初の9を除くと、 [ 7 , 6 , 8 , 3 , 4 , 1 , 0 , 5 , 2 ]となり、本記事冒頭で述べた目標と一致しています。
例2 zazazazaz*
| index | 接尾辞またはLMS部分文字列 |
|---|---|
| 9 | * |
| 7 | az*(LMS部分文字列) |
| 5 | aza(LMS部分文字列) |
| 3 | aza(LMS部分文字列) |
| 1 | aza(LMS部分文字列) |
| 8 | z* |
| 6 | zaz* |
| 4 | zazaz* |
| 2 | zazazaz* |
| 0 | zazazazaz* |
LMS部分文字列に重複があるケースです。
この場合、接尾辞が必ずしも辞書順に並んでいるとは限らないですが、比較する際にLMSのindexのところはLMS部分文字列で、それ以外は接尾辞で比較するとします。そうすると、きちんと辞書順に並んでいることがわかります。
ここで、辞書順に並んでいるLMS部分文字列に番号を振っていきます。
また、同じLMS部分文字列には同じ数字を振ります。
つまり、以下の通りです。
| 番号 | LMS部分文字列 |
|---|---|
* |
1 |
az* |
2 |
aza |
3 |
aza |
3 |
aza |
3 |
この際、重複確認がにならないことを証明します。
それは、重複している部分文字列は隣接しているところにのみ存在するため番号を振るのにはで済みます。
そしてこれを、LMS部分文字列の登場順に並べます。
LMS部分文字列の登場順はaza,aza,aza,az*,*なので、[3,3,3,2,1]となります。
これを、新たな文字列としてみなし、再びいままでの処理を行うことで重複したLMS部分文字列があっても辞書順に並びます。
[3,3,3,2,1]にまたLSを振る。
| 3 | 3 | 3 | 2 | 1 | * |
|---|---|---|---|---|---|
| L | L | L | L | L | S |
| LMS |
LMSを追加する。
*:[5]
先頭から見ていき、型文字を追加する。
*:[ 5 ]
1:[ 4 ]
2:[ 3 ]
3:[ 2 , 1 , 0 ]
LMSを取り除いて(今回は末尾の文字のみがLMSなので取り除かれる文字はない)、末尾からみてS型文字を追加する。
*:[ 5 ]
1:[ 4 ]
2:[ 3 ]
3:[ 2 , 1 , 0 ]
これによって、重複するLMS部分文字列を持つ文字列に対して正しいLMSの辞書順が求まった。
これを基に、最初のLMSを追加するところで順番に入れていき再びSA-ISを実行することで正しいSuffix Arrayが求まります。(それでも求まらない場合はさらに再帰を行い、重複するLMS部分文字列が無くなるまで行う)
また、SA-ISがである理由がこの再帰の量と関係しており、LMSは多くても文字列全体の半分しかなく(例えばzazazazaz*がちょうど半分で、LMSの性質上これ以上存在し得ないため)、再帰を繰り返しても元の文字列の2倍の長さ程度に収まるためです。(実際の実行結果はもうすこし下で紹介します)
ステップ6 再び入れなおす
ステップ4で再帰によって正確なLMSのインデックスの辞書順が分かったので、その順番をもとに、またステップ1から3までを行い、SuffixArrayを完成させます。
これによってTOUKOUDAI*は[7,6,8,3,4,1,0,5,2]と分かる。
また、zazazazaz*は[7,5,3,1,8,6,4,2,0]と分かる。
Verifyするぞ
実装したと思ってるだけで、実際にはバグってたら悲しいので確かめます。
AOJ ALDS1-14-D
ACだ~うれし~。
速度を計るぞ
谷田部へ持ち込まれたソースコードはいったいどんなスコアを叩き出してくれるのか…。
今回長めのテキストファイルが欲しかったので、適当にNCBIから引っ張ってきました。
ちょっとファイルに細工したりしましたが(改行、空白を取り除いたりなど)。
速度は以下の通りになりました。
| サイズ(Byte) | 実行時間(ms) |
|---|---|
| (1万4千) | |
| (14万) | |
| (170万) | (1秒) |
| (1200万) | (8秒) |
| (1.0億) | (83秒) |
(CPU:i5-6600 Mem:16GB Java:openjdk version "11.0.6" 2020-01-14)
一番最後の1.2億文字のケースは、デフォルトの設定で実行するとメモリエラーで落ちてしまったので、メモリ割り当てをモリモリにしています。
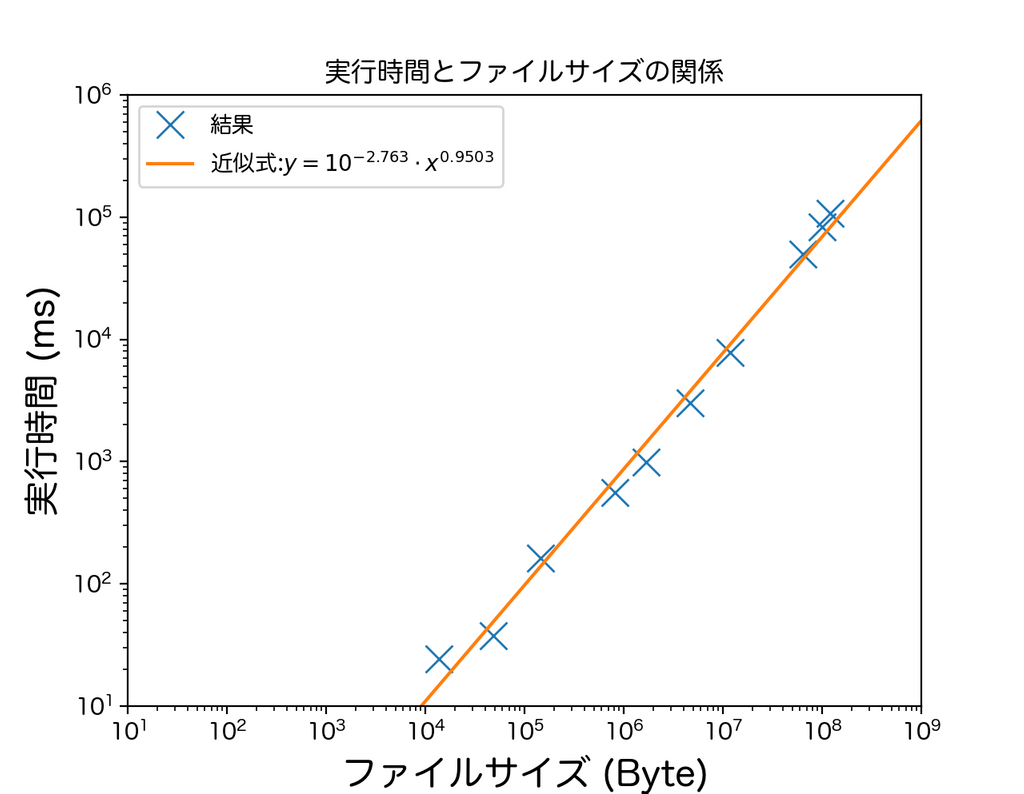
上のファイルサイズと実行時間を両対数グラフにとったもの。これからも分かるようにです。
肩が1を切っていますが、サイズが小さいときのオーバーヘッドによって時間が伸びてると考えられます。
(実装によります。 実装によってはにならない可能性もあります。)
もっと詳しい説明が欲しい方
元の論文をお読みください。
https://ieeexplore.ieee.org/document/5582081
この記事を書くにあたって大変参考になったサイトです(上から参考にした度が高いです)
SA-IS Shogo Computing Laboratory
SA-IS: SuffixArray線形構築 sileのブログ
Suffix Arrayを爆速で構築したら、驚きの結果に…?!?!? knshnbのブログ
SAIS(Suffix Array - Induced Sorting) EchizenBlog-Zwei
あとがき
この記事を執筆するにあたって終始頭のリソースが足りませんでした。つらい…
解説ではあたかも、可変長配列を沢山使うイメージを抱く可能性がありますが、実際のところ固定長配列のみで何とかなります。その際は、インデックス管理に意識するといいと思います。
前回のソルバに続き、今回も@idaten氏に意見をもらいながら完成させました。ありがとうございます。
実装例置いておきますね → 実装例