線形解読法

この記事はtraP Advent Calendar 2018のn日目の記事です。普通のAdvent Calendarなら22日目に相当します。

概要を三行で

SPN構造のブロック暗号の軽い紹介
ブロック暗号に対する線形解読法の紹介
CTF過去問 zer0SPNに対する実際の攻撃

対象読者

暗号の勉強をしたい人
- 保証はしませんがそこそこの理解が得られると思います
CTFのCryptoの勉強をしたい人
- 今後出ることは保証しませんが線形解読法が要求されたときにフラグを見つけられるようになると思います
時間がかかる最適化問題が好きな人
- 線形近似式の構成はマラソン的な要素があるのでそういうテクが生きると思います
暇な人
- 暇が潰せると思います

対象でない読者

実際の暗号を解読したい人
- 実際の暗号は解読が出来ないように世界中のかしこいヒトたちによって設計されてるので期待するだけ無駄です
- あと犯罪です
線形解読法をすでに知っている人
- ﾏｻｶﾘｺﾜｲﾃﾞｽ
- いろいろ間違ってそうなので何かあったらコメントかTwitter@_n_ariまでお願いします……

SPN構造のブロック暗号とは

はじめに今回の食材となるSPN構造のブロック暗号について説明します。
このあたりはインターネット上に日本語での詳しい資料もたくさんあるので、簡単な説明で終わらせます。文中のリンクはWikipediaです。

ブロック暗号とは共通鍵暗号の一種で、暗号化したいデータをブロックと呼ばれる小さなデータ単位に分割し、ブロック1つ1つに対して共通鍵を用いて暗号化関数を適用して、データ全体を暗号化を行う方式です。
実際に使われる場合には単純に分割して単純にくっつけるといろいろまずいので、ブロック単位の暗号化関数の適用方法をいろいろ工夫します(暗号利用モード)。今回は1ブロックの暗号化/復号にのみ興味があるので、この点は省きます。

ブロック暗号にも内部構造によって大きく2種類に分けられます。一つがFeistel構造で、DESやCamelliaといった暗号に用いられる構造です。内部で用いられる非線形関数の逆関数が無くとも復号が行えるのが特徴です。ちなみに読みは「ファイステル構造」で、アインシュタイン(einstein)みたいに"ei"を「アイ」と読みます。
そしてもう一つの構造がSPN構造です。SPNは"Substitution Permutation Network"のことで、訳としてはおおよそ「換字・置換ネットワーク構造」です。ブロックの更に小さい単位に対してSボックス等による換字処理を行い、ブロック全体をビット単位でシャッフルし、鍵を加算する、という処理を繰り返す構造になっています。代表的な共通鍵暗号であるAESなどがSPN構造を採用しています。

以下、SPN構造の詳細を説明します。基本的には鍵の加算→換字→置換を繰り返す構造になっており、データビットが変換される様子は以下の図で表されます。

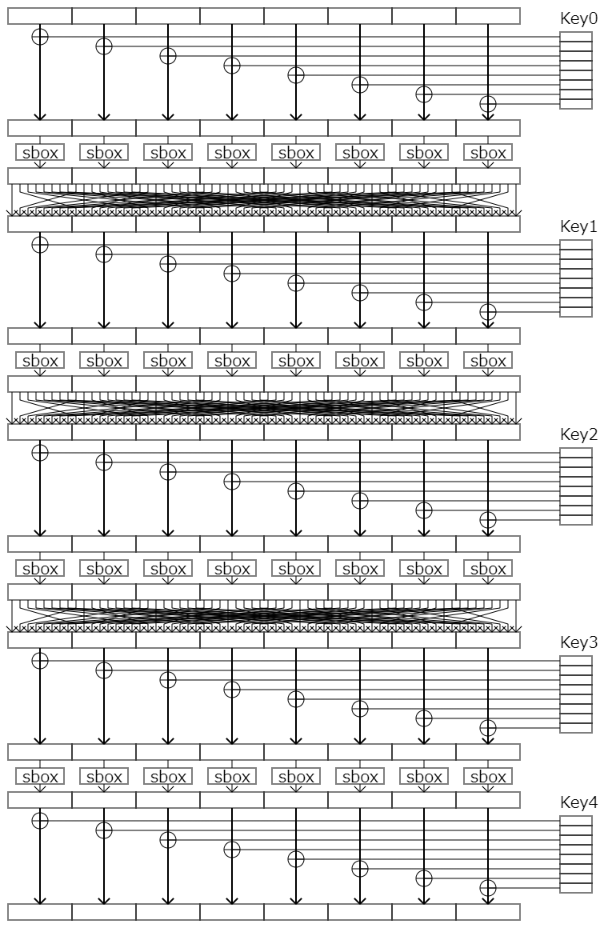
screenshot_00061
(この図は後で出てくるzer0SPNのSPN構造です)

SPN構造では次の処理を繰り返します(暗号方式によって内容や順番、回数などが違います)。1つの繰り返し単位を「ラウンド」と呼びます。

鍵の加算(AddKey)
- データと同じ長さの鍵をXORします
- 一般にラウンドごとに加算される鍵は元の鍵を伸ばしたものが使われます(KeyScheduling)
sboxの適用(Substitute)
- SPN構造の唯一の非線形処理です
- ブロック全体ではなくさらに小さい単位(1バイトなど)に対して処理を行います
- サイズが小さいため換字表を配列で持つことが出来ます
ビット置換(Permutate)
- ブロック全体のビットの順番をシャッフルします
- 置換によって1つのsboxの影響をブロック全体に分散させます
- こちらもサイズが小さいため置換表を配列で持つことが出来ます

このラウンドを何回も繰り返すことで、元のデータに鍵情報を混ぜ、最終的にランダムに見えるような結果を出力します。AESの場合、ラウンド数は10～14となっています。

ブロック暗号の安全性

さてSPN構造について把握したところで、この暗号が本当に安全なのかという議論に移ります。
暗号方式の安全性強度の評価では、「結局どれぐらいの時間をかけたら暗号が解けるの？」という値を用います。つまり、想定される攻撃者がいっぱい時間かけても解けないよ、ということを言えれば安全であると評価できます。

例えば公開鍵暗号方式の一つであるRSA暗号では、安全性が素因数分解の計算困難性(厳密にはRSA仮定)に依存しているため、素因数分解アルゴリズムの計算量によって評価されます。素因数分解アルゴリズムの計算量や、コンピュータの性能向上に応じて、必要とされるビット長などは更新されていきます。

ではブロック暗号ではどうかというと、ブロック暗号を攻撃する手法を頑張って考えて、その手法が必要とする計算量によって評価します。そのうちの主なものが、差分解読法(Differential Cryptanalysis)と線形解読法(Linear Cryptanalysis)です。

差分解読法はその名の通り、入力に差分を与えたときに、出力がどのように変化するかを考察し、その入出力の差から鍵情報を奪う攻撃手法です。入出力が得られるという前提で行える選択平文攻撃です。
詳しくはkatagaitai CTF勉強会の資料がとても参考になります。
katagaitai CTF勉強会 #3 crypto
Katagaitai CTF勉強会 #4 Crypto

線形解読法は、入力と出力の間の線形性を見出すことで鍵情報を奪う攻撃手法です。こちらも同様に選択平文攻撃です。
線形性と言っても、sboxによる換字処理が挟まっているため、線形性は失われています。しかし、確率的な線形性を考えると、データに僅かな偏りが発生していることを観測することが出来、その情報から秘密情報を入手することが出来ます。

線形解読法とは

線形解読法は主に次のようなステップで鍵情報を奪います。

sboxの線形近似式の計算
(N-1)ラウンドの線形近似式の計算
鍵情報の探索

sboxの線形近似式の計算

sboxは非線形な処理を行う換字表です。そのため通常は線形な関係式は導出できません。ただし、sboxへの入力がランダムであると仮定した時、その入出力の間の線形関係式が成立する確率は計算することが出来ます。
例えばsboxを8bit→8bitの変換とすれば、入力は256通り、入出力16bitから関係式の項として取り出す通り数が $2^{16} = 65536$ 通りのため、全ての線形関係式に関して256通りの入力を試し、どれほどの確率で関係式が成立するかを高速に計算することが出来ます。

$X_{i}$ をsboxへの $i$ 番目の入力、 $Y_{i}$ をsboxの $i$ 番目の出力とすれば、

X_{i_{1}} \oplus \dots \oplus X_{i_{n}} = Y_{j_{1}} \oplus \dots \oplus Y_{j_{m}}

という式が成り立つ確率が、

\frac{# { x ∣ y = s b o x ( x ) , ( X _{i_{1}} \cdot x _{i_{1}} ) \oplus \dots \oplus ( X _{i_{n}} \cdot x _{i_{n}} ) = ( Y _{j_{1}} \cdot y _{j_{1}} ) \oplus \dots \oplus ( Y _{j_{m}} \cdot y _{j_{m}} ) }}{2 5 6}

で与えられることになります。

確率を $p$ とした時、 $p - \frac{1}{2}$ を bias と呼びます。暗号的に望ましい線形関係式は出力がランダムに見えてほしいため $p = \frac{1}{2}$ 、すなわちbiasが0であることが望ましいです。

(N-1)ラウンドの線形近似式の計算

SPN構造における唯一の非線形処理部であるsboxに関して線形近似を行ったため、sbox部分を線形近似式で置き換えることで、ラウンド全体、暗号化処理全体に関する線形近似式を構成することが出来ます。
$P_{i}$ を平文の $i$ 番目のビット、 $C_{i}$ を暗号文の $i$ 番目のビット、 $K_{r, i}$ を $r$ ラウンド目の鍵の $i$ 番目のビットとすると、

P_{i_{1}} \oplus \dots \oplus P_{i_{n}} \oplus C_{j_{1}} \oplus \dots \oplus C_{j_{m}} = K_{r_{1}, k_{1}} \oplus \dots \oplus K_{r_{l}, k_{l}}

という線形近似式を構成することになります。なお、この時着目しているビットの流れをtrailと呼んだりします。

この線形近似式の成立確率は、使用したsbox線形近似式の確率のbiasの総積の形になります(piling-up lemma)。具体的には使用した $i$ 個目のsbox線形近似式のbiasを $b_{i}$ とすれば

(線形近似式の bias) = 2^{n - 1} i \prod b_{i}

として計算されます。

全体の線形近似式の探索においては、全ての線形近似式を探索することは不可能なため、ヒューリスティック探索を行うことになります。このあたりに関してはMILPソルバが適用な形にしたりとかビームサーチを使ったりとかいろいろで対応できると思います(マラソン要素)。

鍵情報の探索

さて、有意なbiasの存在する確率近似式を得ることが出来ました。これを用いて秘密鍵の情報を取得します。
まず線形解読法の前提として、十分な数の平文・暗号文ペアが得られていることが条件になっています。これは後述のアルゴリズムの成功確率によりますが、biasの逆数の二乗個のペアが存在すると高い確率で攻撃が成功します。

線形近似式の使い方ですが、Nラウンドの近似式は $P \oplus C = K$ といった形をしていて、偏った確率でこの式が成立するため、実際の平文・暗号文ペアから左辺が1になる確率を計算することで、右辺の値を高確率で推定することが可能となります。これが1つ目の使い方です。Matsui's Algorithm 1と呼ばれたりします。

もう一つがMatsui's Algorithm 2です。こちらは入力もしくは出力の少ない(N-1)ラウンドの近似式を利用します。
例えば、次の図のような第二ラウンドから始まる線形近似式を考えます。

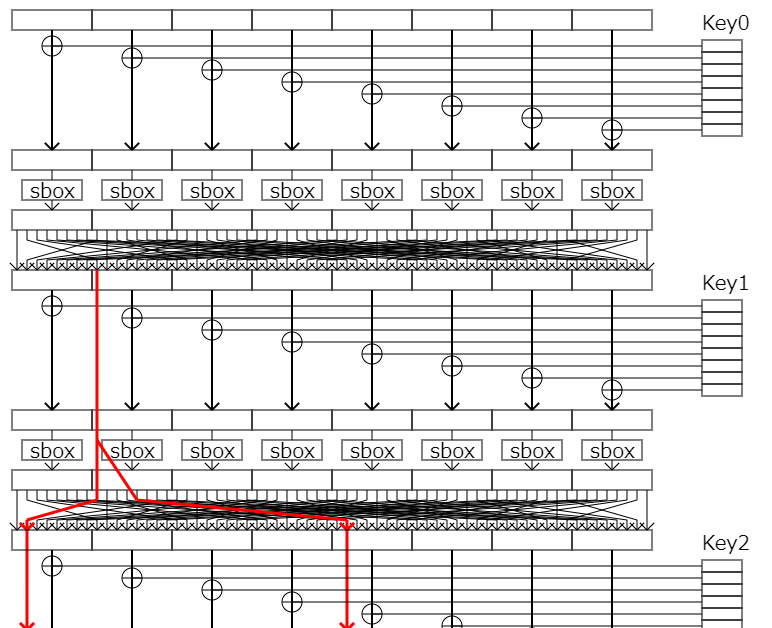
screenshot_00063

この時、第二ラウンドに入力されるビットと出力ビット(つまり暗号文)のペアが正しい鍵で生成されたペアによるものと等しい場合、求められていた近似式のbiasだけ結果が偏ります。

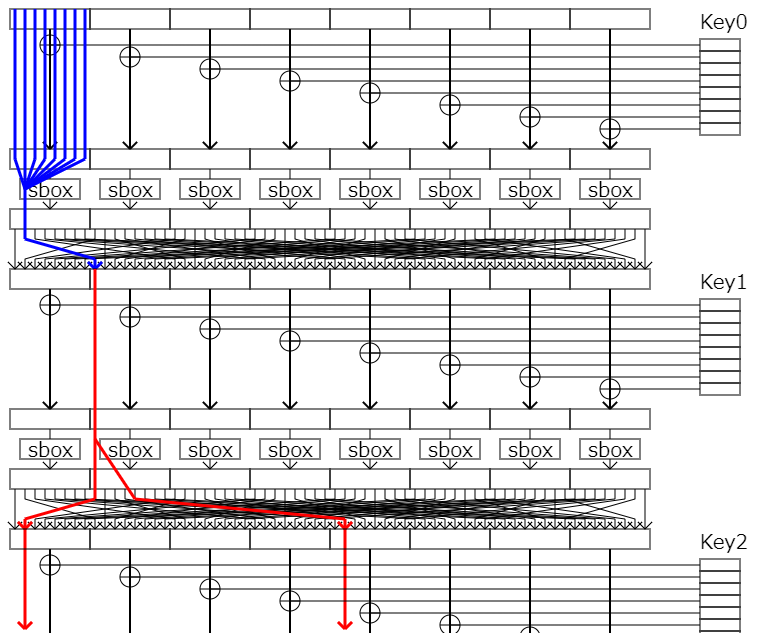
この入力ビットを第一ラウンドまで逆算すると次の図の青い線のようになります。

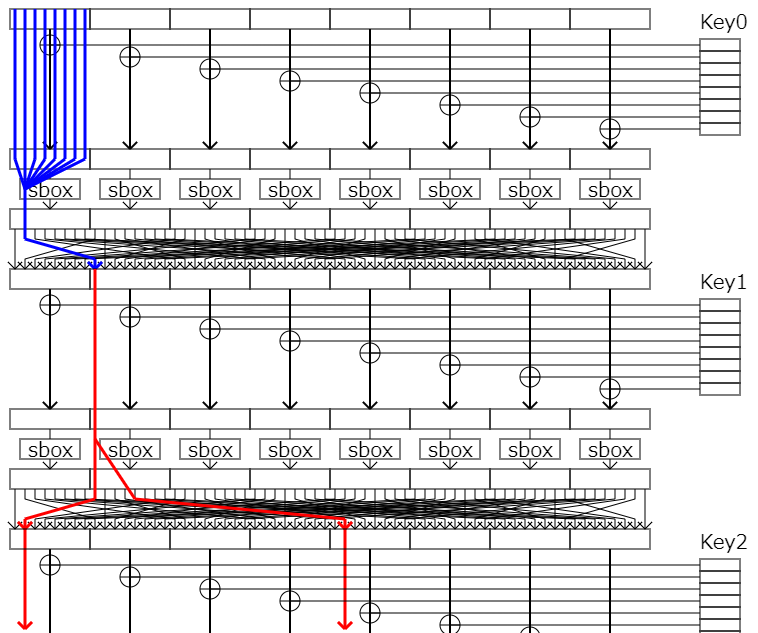
screenshot_00064

ここで、一番上から平文を流しつつ、第一ラウンドの鍵(Key0)の1つ目のパーツを推定してみましょう。
もしこのパーツが正しい鍵のものと同じであった場合、第一ラウンドのsboxに入力される値は当然正しい鍵で暗号化したときのものと確率1で一致します。そのため、第二ラウンドからの線形近似式はそのままのbiasで偏ります。
一方でこのパーツが正しい鍵のもので無かった場合、第一ラウンドのsboxに入力される値は異なった値とxorされるため異なってしまいます。このとき、第二ラウンドへの入力が、正しい鍵で暗号化した時の入力と一致する確率というのは、第一ラウンドのsboxの線形近似確率の分だけbiasが減少してしまいます。つまり、第二ラウンドからの線形近似式は元のbiasより小さな値になります。
よって、鍵(の一部)を全通り試すと、一番結果が偏った時の鍵が正しい鍵(の候補)ということが分かります。
これを繰り返し、すでに得た鍵情報も活用して全ての鍵情報を入手することが出来ます。

CTF過去問: zer0SPNの解法

0CTF 2018 Qualsにて、zer0SPNというCrypto問題が出ました。4ラウンドのSPN構造ブロック暗号で、65536個の平文・暗号文ペアが与えられているので鍵を答えてください、という問題です。
構造は先にSPN構造の例として示したものです。また元の鍵はKey0で、Key1～Key4はKeyScheduleアルゴリズムによってKey0から生成された情報です。

問題のファイルは以下(検索して出てきたもの)。
https://github.com/harrier-lcc/ctf-writeups/blob/master/2018/0ctf-quals/zer0SPN/zer0SPN.py
https://github.com/harrier-lcc/ctf-writeups/blob/master/2018/0ctf-quals/zer0SPN/dataSPN

sboxと置換表(ptable)は以下のとおりです。どちらも入力 i に出力 sbox[i], ptable[i] が対応します。

int sbox[256] = {
  62, 117, 195, 179, 20, 210, 41, 66, 116, 178, 152, 143, 75, 105, 254, 1, 
  158, 95, 101, 175, 191, 166, 36, 24, 50, 39, 190, 120, 52, 242, 182, 185, 
  61, 225, 140, 38, 150, 80, 19, 109, 246, 252, 40, 13, 65, 236, 124, 186, 
  214, 86, 235, 100, 97, 49, 197, 154, 176, 199, 253, 69, 88, 112, 139, 77, 
  184, 45, 133, 104, 15, 54, 177, 244, 160, 169, 82, 148, 73, 30, 229, 35, 
  79, 137, 157, 180, 248, 163, 241, 231, 81, 94, 165, 9, 162, 233, 18, 85, 
  217, 84, 7, 55, 63, 171, 56, 118, 237, 132, 136, 22, 90, 221, 103, 161, 
  205, 11, 255, 14, 122, 47, 71, 201, 99, 220, 83, 74, 173, 76, 144, 16, 
  155, 126, 60, 96, 44, 234, 17, 215, 107, 138, 159, 183, 251, 3, 198, 0, 
  89, 170, 131, 151, 219, 29, 230, 32, 187, 125, 134, 64, 12, 202, 164, 247, 
  25, 223, 222, 119, 174, 67, 147, 146, 206, 51, 243, 53, 121, 239, 68, 130, 
  70, 203, 211, 111, 108, 113, 8, 106, 57, 240, 21, 93, 142, 238, 167, 5, 
  128, 72, 189, 192, 193, 92, 10, 204, 87, 145, 188, 172, 224, 226, 207, 27, 
  218, 48, 33, 28, 123, 6, 37, 59, 4, 102, 114, 91, 23, 209, 34, 42, 
  2, 196, 141, 208, 181, 245, 43, 78, 213, 216, 232, 46, 98, 26, 212, 58, 
  115, 194, 200, 129, 227, 249, 127, 149, 135, 228, 31, 153, 250, 156, 168, 110
};
int ptable[64] = {
  0, 8, 16, 24, 32, 40, 48, 56, 
  1, 9, 17, 25, 33, 41, 49, 57, 
  2, 10, 18, 26, 34, 42, 50, 58, 
  3, 11, 19, 27, 35, 43, 51, 59, 
  4, 12, 20, 28, 36, 44, 52, 60, 
  5, 13, 21, 29, 37, 45, 53, 61, 
  6, 14, 22, 30, 38, 46, 54, 62, 
  7, 15, 23, 31, 39, 47, 55, 63
};

screenshot_00061

置換表は図で示したとおりで、各ラウンドで任意のバイト間でビットが移動します。一方sboxは線形近似式の成立確率を計算するとかなり偏っているため、線形解読法が適用できます。

具体的には以下のようなtrailが考えられます(ビームサーチみたいなもので探索しました)。trailInが入力ビット位置、trailOutが出力ビット位置、targetKeyIdが探索する鍵のバイト位置です。

  // bias: 0.01149997, key block: 1
  trailIn.push_back(vector<int>({1}));
  trailOut.push_back(vector<int>({62,60,56,30,28,24}));
  targetKeyId.push_back(1);
  // bias: 0.01796870, key block: 1
  trailIn.push_back(vector<int>({9}));
  trailOut.push_back(vector<int>({54,52,48,6,4,0}));
  targetKeyId.push_back(1);
  // bias: 0.00667572, key block: 2
  trailIn.push_back(vector<int>({18}));
  trailOut.push_back(vector<int>({14,8}));
  targetKeyId.push_back(2);
  // bias: 0.01796870, key block: 2
  trailIn.push_back(vector<int>({10}));
  trailOut.push_back(vector<int>({54,48,6,0}));
  targetKeyId.push_back(2);
  // bias: 0.00807762, key block: 6
  trailIn.push_back(vector<int>({54}));
  trailOut.push_back(vector<int>({14,8}));
  targetKeyId.push_back(6);
  // bias: 0.01124442, key block: 6
  trailIn.push_back(vector<int>({6}));
  trailOut.push_back(vector<int>({62,56,30,24}));
  targetKeyId.push_back(6);

  // bias: 0.02129555, key block: 0, 1, 6
  trailIn.push_back(vector<int>({48,49,54}));
  trailOut.push_back(vector<int>({14,11,10,8}));
  targetKeyId.push_back(0);
  // bias: 0.03705546, key block: 0, 1, 6
  trailIn.push_back(vector<int>({8,9,14}));
  trailOut.push_back(vector<int>({54,51,50,48,6,3,2,0}));
  targetKeyId.push_back(0);
  // bias: 0.00801921, key block: 1, 5
  trailIn.push_back(vector<int>({1,5}));
  trailOut.push_back(vector<int>({63,62,61,60,59,31,30,29,28,27}));
  targetKeyId.push_back(5);
  // bias: 0.01233965, key block: 5, 6
  trailIn.push_back(vector<int>({13,14}));
  trailOut.push_back(vector<int>({55,53,52,51,49,7,5,4,3,1}));
  targetKeyId.push_back(5);
  // bias: 0.01986027, key block: 2, 6, 7
  trailIn.push_back(vector<int>({10,14,15}));
  trailOut.push_back(vector<int>({53,52,51,5,4,3}));
  targetKeyId.push_back(7);
  // bias: 0.02373923, key block: 1, 2, 6, 7
  trailIn.push_back(vector<int>({9,10,14,15}));
  trailOut.push_back(vector<int>({54,53,51,48,6,5,3,0}));
  targetKeyId.push_back(7);

  // bias: 0.01925732
  trailIn.push_back(vector<int>({8,10,12,14,15}));
  trailOut.push_back(vector<int>({54,53,52,6,5,4}));
  targetKeyId.push_back(4);
  // bias: 0.02028296
  trailIn.push_back(vector<int>({8,9,10,12,14,15}));
  trailOut.push_back(vector<int>({53,48,5,0}));
  targetKeyId.push_back(4);
  // bias: 0.01951218
  trailIn.push_back(vector<int>({48,51,53,54}));
  trailOut.push_back(vector<int>({15,14,13,12,11}));
  targetKeyId.push_back(3);
  // bias: 0.02405763
  trailIn.push_back(vector<int>({0,3,5,6}));
  trailOut.push_back(vector<int>({63,62,61,60,59,31,30,29,28,27}));
  targetKeyId.push_back(3);

今回は $2^{16}$ 個の平文・暗号文ペアが与えられているため、 $2^{- 8} = 0.00390625$ 以上のbiasがあると高確率で正しい鍵情報が得られます。
最初の6つは鍵情報として1バイトのみを仮定しますが、続く6つの線形近似式ではそれまでに得た3つの鍵バイトを既知のものとして構成するため、入力ビット数を増やすことが出来、それに伴い候補となる線形近似式も増えるため、より高いbiasの式が見つかりやすくなります。最後の4つは既知となった6つの鍵バイトを利用しています。

1つ目のtrailを図示したものが以下の図です。
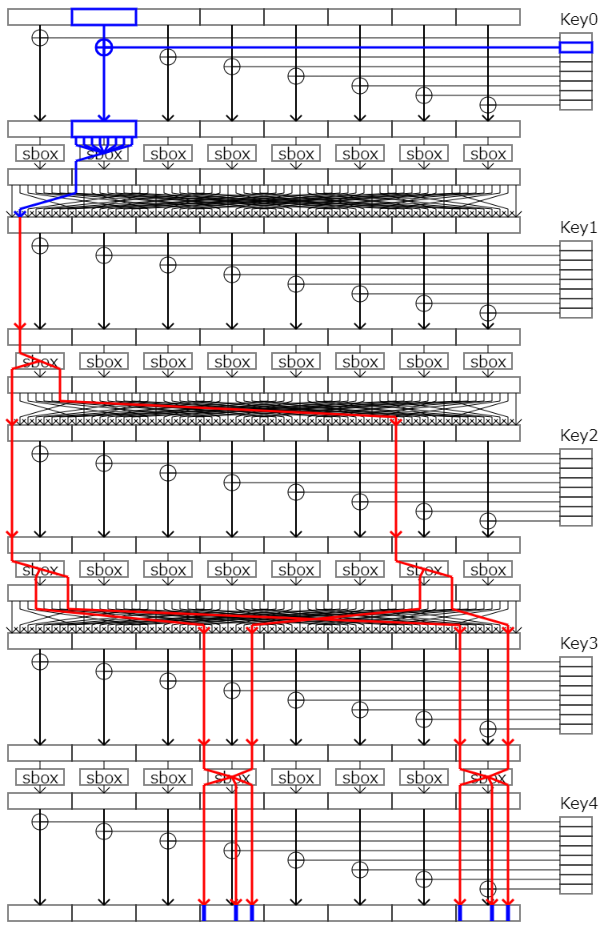
screenshot_00065

今回見つけた中で一番biasの大きい(0.03705546)8つ目のtrailを図示したものが以下の図です。鍵バイトを3つ使うため、内2つの鍵バイトを確定させてから残りの1つの鍵バイトを推定するために使います(もしくは、鍵バイト2つ程度の全探索なら現実的な時間で終わるため、1つを確定させてからでも使えなくは無いです)。
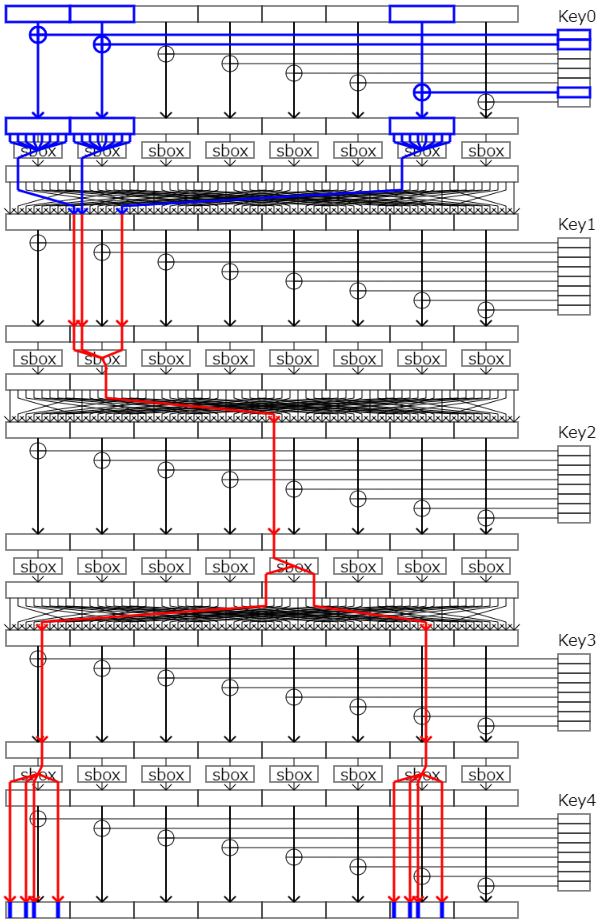
screenshot_00068

これらの線形近似式によって鍵情報を探索すると、以下のような結果が得られます(各trailに対して鍵バイト候補を偏りでランク付けして5位まで表示)。実際に暗号化テストをしてみると各平文・暗号文ペアが正しく生成されるため、正しく鍵情報が得られたことが分かります。

blockId=1, #1:66(0.01113892), #2:f9(0.00599670), #3:2d(0.00576782), #4:05(0.00567627), #5:43(0.00454712),
blockId=1, #1:66(0.01788330), #2:14(0.01144409), #3:6f(0.01127625), #4:a6(0.01126099), #5:a1(0.01109314),
blockId=2, #1:7e(0.01092529), #2:ba(0.00808716), #3:e9(0.00785828), #4:1b(0.00776672), #5:36(0.00762939),
blockId=2, #1:7e(0.01599121), #2:17(0.01205444), #3:d0(0.01165771), #4:05(0.01066589), #5:77(0.01028442),
blockId=6, #1:33(0.01046753), #2:66(0.00613403), #3:87(0.00598145), #4:05(0.00561523), #5:e9(0.00552368),
blockId=6, #1:33(0.01068115), #2:31(0.00579834), #3:85(0.00527954), #4:d6(0.00524902), #5:c1(0.00521851),
blockId=0, #1:48(0.02020264), #2:35(0.00933838), #3:d4(0.00881958), #4:b3(0.00791931), #5:1e(0.00787354),
blockId=0, #1:48(0.03933716), #2:33(0.02023315), #3:5a(0.01957703), #4:41(0.01776123), #5:3a(0.01696777),
blockId=5, #1:fb(0.00807190), #2:15(0.00643921), #3:b1(0.00590515), #4:2e(0.00588989), #5:c6(0.00581360),
blockId=5, #1:fb(0.01374817), #2:32(0.00947571), #3:49(0.00927734), #4:de(0.00842285), #5:f2(0.00796509),
blockId=7, #1:83(0.02220154), #2:24(0.01536560), #3:8a(0.01388550), #4:f6(0.01367188), #5:ed(0.01335144),
blockId=7, #1:83(0.02500916), #2:f8(0.01560974), #3:91(0.01502991), #4:8a(0.01492310), #5:56(0.01353455),
blockId=4, #1:a5(0.01843262), #2:eb(0.01119995), #3:ee(0.01043701), #4:55(0.01040649), #5:1e(0.00997925),
blockId=4, #1:a5(0.01925659), #2:b7(0.01205444), #3:de(0.01191711), #4:3d(0.01116943), #5:33(0.01098633),
blockId=3, #1:c1(0.01878357), #2:f2(0.00952148), #3:99(0.00851440), #4:1b(0.00833130), #5:ca(0.00827026),
blockId=3, #1:c1(0.02320862), #2:70(0.01116943), #3:13(0.00981140), #4:f8(0.00975037), #5:9e(0.00959778),
key : 48667ec1a5fb3383

なお、自分で鍵を設定し、平文・暗号文ペアを生成してテストしたところ、一部線形近似式で正しい鍵バイトでない値が1位に来ることがありました。このようなことは確率的に十分ありえますが、複数の線形近似式で試すと正しい候補はほぼ全ての線形近似式で上位に入るため、そこから正しい情報が推測できます(といったことに関する厳密な研究もあると思いますが詳しくは読んでいないです)。

まとめ

以上で線形解読法の紹介を終わらせていただきます。いかがだったでしょうか。
僅かな偏りを攻める攻撃でとてもかっこいいと個人的には思いました。

ちなみに当然ですが、現在世界で使用されているブロック暗号では、線形解読法や差分解読法を用いても鍵情報を奪うことは鍵の全探索よりも効率が悪い、ということを保証しているものがほとんどです。安心してブロック暗号を使いましょう。
(もちろんこれからまた新種の攻撃手法が出てくる可能性もありますが……)

参考文献

0CTF 2018 Quals – zer0SPN (Crypto 550) | More Smoked Leet Chicken
0CTF/TCTF Quals zer0SPN - Harrier's blog
Linear Cryptanalysis Method for DES Cipher

おまけ

実際にC++で解読アルゴリズムを実装したのが以下です。競プロの癖でREPマクロとか統一感の無い変数名とか関数化されてないコードのコピペとかが大量にあります。

https://gist.github.com/n-ari/9624222c1575295cb1534231ad9e4027