本記事は、traP アドベントカレンダー 2018 の 60日目 の記事です。
明後日が最終日らしいので、たぶん traP におけるクリスマスは 12/62 なんでしょうね。

当初、この記事では J 言語の話をしようと思ってたのですが、難解なリファレンスを読み切れずに断念しました……

そこで、この記事ではわたし youjo_tape が知っている 素数 に関する雑学を書き並べます。
需要とかそういうのは知りません

1. 日付ネタ

今日は 12/23 ですね。1223 は小さい方から数えて 200 番目 の素数です。
このように mmdd の形式で記述したときに素数になる日付は、今年はあと 1229, 1231 の 2 個だけです。
これに関連して（？）、10000 以下の素数の個数が 1229 個だったりします。

ところで、アドベントカレンダーといえば、本来は「来たるクリスマス（12/25）を迎えるまでの日数を数えるため」のものでした。
1225 といえば、やはり 平方数 で有名ですよね。$1225=35^2$ です。
しかし実は、1225 は 三角数 でもあります。

三角数とは、その数だけ点を並べるとちょうど三角形がつくれるような数です。
小さい順に書けば、$1,3,6,10,\cdots$ となりますね。それぞれ、以下の三角形に対応します：

o   o     o       o
   o o   o o     o o
        o o o   o o o
               o o o o

この図から察せるように、$n$ 番目の三角数は $\sum _{i=1}^{n}i=\frac{n(n+1)}{2}$ と表せますね。
したがって、$1225=\frac{49\times 50}{2}$ なので、$1225$ は 49 番目の三角数とわかります。

ちなみに、平方数かつ三角数であるような数は 平方三角数 と呼ばれることがあります。なんとも珍しそうに思えますが、平方三角数は無限に存在することがわかっています。具体的に、$n$ 番目の平方三角数は

$$\frac{1}{32}{\left({\left(1+\sqrt{2}\right)}^{2n}-{\left(1-\sqrt{2}\right)}^{2n}\right)}^2$$

で与えられることを、あの Euler さんが示していました。

素数に話を戻しますが、今日は 2018/12/23 ですね。
なんと、20181223 も素数です！ ちなみに、この次の素数は 20181229 で、これも yyyymmdd 形式の日付と解釈できますね。

2. フェルマーの二平方定理

とは、以下のような定理です：

素数 $p$ は、$4$ で割って $1$ 余るならば、ある自然数 $x,y$ が存在して $p=x^2+y^2$ と表せる。^[1]

証明の方法は様々ですが、そのひとつに Zagier さんが与えた以下のようなものがあります：

有限集合 $S=\{(x,y,z)\in {\mathbb{N}}^3\mid x^2+4yz=p\}$ 上の対合

$$(x,y,z)\mapsto \{\begin{array}{ll}(x+2z,z,y-x-z)& (x<y-z)\\ (2y-x,y,x-y+z)& (y-z<x<2y)\\ (x-2y,x-y+z,y)& (2y<x)\end{array}$$

は必ず一個の不動点を持つから、集合 $S$ の元の個数は奇数であり、対合 $(x,y,z)\mapsto (x,z,y)$ も不動点を持つ。

この一文で証明が完結しています。
しかし、行間が広すぎて、いったいどこがどう証明になっているのかすらサッパリですね。
順を追って行間を埋めていきましょう。

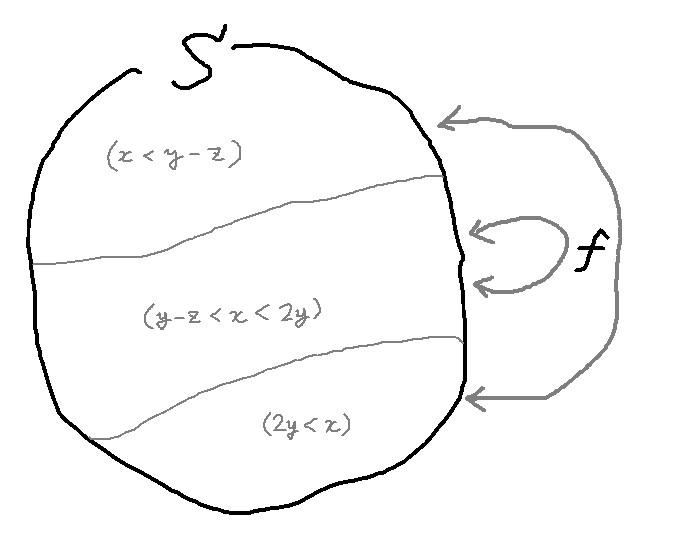
「有限集合 $S=\{\cdots \}$」

$x^2+4yz=p$ を満たすような $(x,y,z)\in {\mathbb{N}}^3$ は明らかに高々有限個しかありません。大雑把に見ても $x,y,z<p$ が必要ですもんね。
したがって、$S$ は確かに有限集合です。

「… 上の対合 …」

対合とは、ざっくりと言えば「2 回変換すると元もとの元げんに戻るような変換」です。
証明中で定められている対応を $f:S\to S$ とおいて、これが正しく対合になっているか確認してみましょう：

まず、$f$ が 写像 として well-defined であるかどうかの確認からしなければなりませんね。定義中の 3 つの場合分け：

$$x<y-z,y-z<x<2y,2y<x$$

をよく見てみましょう。常に $y-z<2y$ であるので、この場合分けは直感的には「$y-z$ および $2y$ と比較したときに、$x$ はどこにいるのか」という風に解釈できます。
しかし、範囲の重複こそないものの、$x=y-z$ または $x=2y$ のときに $f$ が定まっていないように見えますね。ですが、

• $x=y-z$ のとき、$x^2+4yz=(y-z{)}^2+4yz=(y+z{)}^2$
• $x=2y$ のとき、$x^2+4yz=4y^2+4yz=4y(y+z)$

であるので、これらの場合には $x^2+4yz$ が素数になる、すなわち $x^2+4yz=p$ が成り立つことはありません。この対偶をとれば、$S$ 上では常に $x\ne y-z$ かつ $x\ne 2y$ であることがわかるので、確かに $f$ は $S$ 上の写像として well-defined であることが従います。

では次に、$f$ が 変換 ならびに 対合 になっているか確認しましょう。3 つの場合に分けて調べればよいですね：

• $x<y-z$ のとき、

  $$(x^{\prime },y^{\prime },z^{\prime }):=f(x,y,z)=(x+2z,z,y-x-z)$$

  とおくと、

  $$x^{\prime 2}+4y^{\prime }{z}^{\prime }=(x+2z{)}^2+4z(y-x-z)=x^2+4yz=p$$

  であるから、$(x^{\prime },y^{\prime },z^{\prime })\in S$ である。また、$2y^{\prime }=2z<x^{\prime }=x+2z$ なので、

  $$f(x^{\prime },y^{\prime },z^{\prime })=(x^{\prime }-2y^{\prime },x^{\prime }-y^{\prime }+z^{\prime },y^{\prime })=(x,y,z)$$

  が成り立つ。
• $y-z<x<2y$ のとき、

  $$(x^{\prime },y^{\prime },z^{\prime }):=f(x,y,z)=(2y-x,y,x-y+z)$$

  とおくと、

  $$x^{\prime 2}+4y^{\prime }{z}^{\prime }=(2y-x{)}^2+4y(x-y+z)=x^2+4yz=p$$

  であるから、$(x^{\prime },y^{\prime },z^{\prime })\in S$ である。また、$y^{\prime }-z^{\prime }=2y-x-z<x^{\prime }=2y-x<2y^{\prime }=2y$ なので、

  $$f(x^{\prime },y^{\prime },z^{\prime })=(2y^{\prime }-x^{\prime },y^{\prime },x^{\prime }-y^{\prime }+z^{\prime })=(x,y,z)$$

  が成り立つ。
• $2y<x$ のとき、

  $$(x^{\prime },y^{\prime },z^{\prime }):=f(x,y,z)=(x-2y,x-y+z,y)$$

  とおくと、

  $$x^{\prime 2}+4y^{\prime }{z}^{\prime }=(x-2y{)}^2+4(x-y+z)y=x^2+4yz=p$$

  であるから、$(x^{\prime },y^{\prime },z^{\prime })\in S$ である。また、$x^{\prime }=x-2y<y^{\prime }-z^{\prime }=x-2y+z$ なので、

  $$f(x^{\prime },y^{\prime },z^{\prime })=(x^{\prime }+2z^{\prime },z^{\prime },y^{\prime }-x^{\prime }-z^{\prime })=(x,y,z)$$

  が成り立つ。

以上より、確かに $f$ は $S$ 上の対合であることが示せました。

「… は必ず一個の不動点を持つから、」

変換 $\phi$ の不動点とは、変換により変化しない（すなわち、$\phi (a)=a$ となる）点のことです。
これより、対合 $f$ の不動点を求めるには、$f(x,y,z)=(x,y,z)$ を解けばよいことになります。

ここで、$f$ の不動点 $(x,y,z)$ は、（存在すれば）必ず $y-z<x<2y$ を満たします。

理由を述べます。先ほど $f$ が対合であることを示したとき、

• $x<y-z$ なる点 $(x,y,z)$ は、$2y^{\prime }<x^{\prime }$ なる点 $(x^{\prime },y^{\prime },z^{\prime })$ に
• $2y<x$ なる点 $(x,y,z)$ は、$x^{\prime }<y^{\prime }-z^{\prime }$ なる点 $(x^{\prime },y^{\prime },z^{\prime })$ に

写されてしまうことがわかりました。ということは、「$x<y-z$ かつ $2y<x$」となることはあり得ないので、このいずれの場合も $(x,y,z)=(x^{\prime },y^{\prime },z^{\prime })$ は成り立ちません。

不動点は「$f$ による変換で条件が変わらない場所」にしか存在しえないよね、ということです：

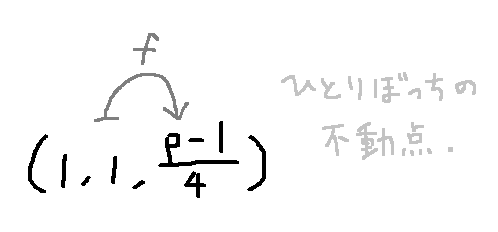
したがって、$y-z<x<2y$ としてよく、このとき

$$\begin{array}{rl}f(x,y,z)=(x,y,z)& ⟺(2y-x,y,x-y+z)=(x,y,z)\\ & ⟺\{\begin{array}{l}2y-x=x\\ y=y\\ x-y+z=z\end{array}\\ & ⟺x=y\end{array}$$

となります。さらに、$(x,y,z)$ は $S$ 上の点でなければならないことから、

$$\begin{array}{rl}{x}^2+4yz=p& ⟺x^2+4xz=p\\ & ⟺x(x+4z)=p\end{array}$$

が必要です。したがって、$x+4z>1$ であるので、$p$ が素数である ことを考えると $x=1,x+4z=p$ でなければなりません。
以上をまとめると、$f$ の不動点は唯一で：

$$\left(1,1,\frac{p-1}{4}\right)$$

と求まります。$p$ は $4$ で割って $1$ 余る素数 なので、$\frac{p-1}{4}$ は自然数であり、たしかにこの点が $S$ に含まれていることがわかりますね。

「集合 $S$ の元の個数は奇数であり、」

$S$ の元は、対合 $f$ によってペアをなしています。

不動点ではない点たち：

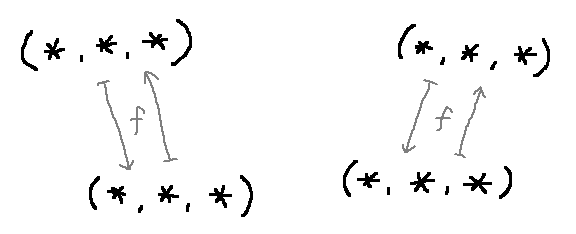
ただし、$f$ の不動点 $\left(1,1,\frac{p-1}{4}\right)$ だけは、いわば "自分自身とペアをなしている" ことになります。

不動点：

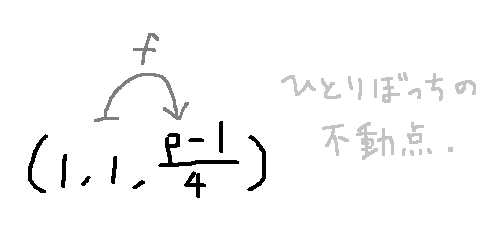
$f$ の不動点がちょうど 1 つだけ存在することは先ほど示していたので、$S$ が有限集合であることも踏まえると、$S$ の元は奇数個であることがわかりますね。

「対合 $(x,y,z)\mapsto (x,z,y)$ も不動点を持つ」

文脈を汲み取ると、この対合は $S$ 上で考えているものでしょうね。
すなわち、これをもう少し丁寧に記述するならば、「対合 $g:S\ni (x,y,z)\mapsto (x,z,y)\in S$」となるでしょうか。

$x^2+4yz=p$ という条件が $y,z$ に関して対称になっていることから、「$y,z$ を入れ替える」写像である $g$ が $S$ 上の変換になっていることがわかります。また、$g$ が対合であることも明らかですね。

さて、この $g$ が不動点を持たないと仮定します。すると、$S$ の元は すべて 対合 $g$ により「2元1組の」ペアにすることができます。すると、$S$ は有限集合であったので、$S$ の元は偶数個ということになりますが、先ほど「$S$の元は奇数個」と示したので、矛盾が生じます。
ゆえに、$g$ は不動点を持ちます。

「。」

証明文はここで終わりですが、「$p$ が 2 つの平方数の和で表せる」という結論にはまだ達していませんね。「後はわかるでしょ？」とばかりに省略されてしまったのです。

仕方がないので、最後の行間を埋めましょう。
$g$ が不動点を持つということなので、不動点のひとつを $(x,y,z)$ とおきます。すると、不動点の定義より、

$$\begin{array}{rl}g(x,y,z)=(x,y,z)& ⟺(x,z,y)=(x,y,z)\\ & ⟺\{\begin{array}{l}x=x\\ z=y\\ y=z\end{array}\\ & ⟺y=z\end{array}$$

がわかります。そして、$(x,y,z)=(x,y,y)$ が不動点であることから、とくに $(x,y,y)\in S$ であることも従うので、

$$x^2+4y^2=p$$

すなわち、$x^2+(2y{)}^2=p$ が成り立ちます。これが求める表現です。■

丁寧に記述したら、めっちゃ長くなってしまいました。
しかし、なんでこんな証明を思いつくに至ったのでしょうね。対合 $f$ とかどっから出てきたのよ。

3. 素数の無限性

素数は無限に存在する。

言わずと知れた有名な定理ですね。これにも様々な証明があります。

ところで、唐突に話を位相空間論に移すのですが、みなさん「位相」ってご存知ですか？
知らない方には申し訳ないのですが、この項は「位相を知ってる人」向けの内容になっています。

とはいえ、完全に突き放すのも申し訳ないので、主要な定義だけ書いておきますね：

集合 $X$ に対し、その部分集合の集合 $\mathcal{O}\subset \mathcal{P}(X)$ が $X$ 上の 位相 であるとは、以下の 3 条件を満たすことを言います：

1. $\varnothing ,X\in \mathcal{O}$
2. $U_1,U_2\in \mathcal{O}⟹U_1\cap U_2\in \mathcal{O}$
3. $U_{\lambda }\in \mathcal{O}(\forall \lambda \in \Lambda )⟹\bigcup _{\lambda \in \Lambda }{U}_{\lambda }\in \mathcal{O}$

2 番目の条件は「$\mathcal{O}$ 内の 有限個の 共通部分は $\mathcal{O}$ 内に収まる」、3 番目の条件は「$\mathcal{O}$ 内の 任意個の 和集合は $\mathcal{O}$ 内に収まる」、ということをそれぞれ言っています。^[2]

位相 $\mathcal{O}$ に属する集合 $U$ は、$X$ の 開集合 と呼ばれます。この名前からわかるように、「位相」というのは、ユークリッド空間なんかにおける「開集合」の一般化となっています。
たとえば、1 次元ユークリッド空間 $X=\mathbb{R}$ の開集合全体を $\mathcal{O}$ とすれば、上に示した 3 条件が成り立っていることが示せます。

さて、「開集合」があるなら、とうぜん「閉集合」もあります。
$S\subset X$ が（$X$ の）閉集合 であるとは、その補集合 $S^c=X\setminus S$ が開集合であることをいいます。

そして、補集合全体の集合を $\mathcal{F}$ とおくと、$\mathcal{F}$ に対して次の 3 条件が成り立っています：

1. $\varnothing ,X\in \mathcal{F}$
2. $F_1,F_2\in \mathcal{F}⟹F_1\cup F_2\in \mathcal{F}$
3. $F_{\lambda }\in \mathcal{F}(\forall \lambda \in \Lambda )⟹\bigcap _{\lambda \in \Lambda }{F}_{\lambda }\in \mathcal{F}$

さっきのとの違いは、$\cup ,\cap$ がひっくり返っていることですね。

詳しい説明は位相幾何学に関する書籍や講義に譲るとして、本題に移ります。
なんと、「位相」の概念を用いることで、素数の無限性を証明できる のです！

まず、$a,b\in \mathbb{Z}(a\ne 0)$ に対し、$a\mathbb{Z}+b:=\{an+b\mid n\in \mathbb{Z}\}$ と表記することにします。
特に $b=0$ の場合は、単に $a\mathbb{Z}$ とだけ書くことにしましょう。

例えば、$3\mathbb{Z}+1=\{\cdots ,-5,-2,1,4,7,\cdots \}$、みたいな感じです。

さて、これを用いると、$\mathbb{P}$ を素数全体の集合として、

$$\mathbb{Z}\setminus \{\pm 1\}=\bigcup _{p\in \mathbb{P}}p\mathbb{Z}\cdots (\ast )$$

が成り立ちます。$\pm 1$ 以外の任意の整数は、ある素数で割り切ることができるためですね。

いったんこれは置いといて、$\mathcal{O}$ を、「集合 $\{a\mathbb{Z}+b(\subset \mathbb{Z})\mid a,b\in \mathbb{Z},a\ne 0\}$ の任意個（0 個でもよい）の元の和集合全体」とします。
「0 個の集合の和集合」って何だよ、って思われるかもしれませんが、これは「空和」という考え方により $\varnothing$ であると約束されています。

余談ですが、空和の考え方はプログラミングなんかにも現れますね。例えば、よくある「総和を求めるプログラム」は、

int sum = 0;
for(int i = 0; i < 100; i ++) sum += i;

のように記述されますが、この冒頭で int sum = 0; としているのもコレです。

さて、こうして定められた $\mathcal{O}$ は、$\mathbb{Z}$ 上の位相になっています。
実際に示してみましょう…… と言いたいところなのですが、2. とか結構面倒なので、証明は読者にお任せします。

さて、$\mathcal{O}$ の定め方より、$\mathcal{O}$ の元は $\varnothing$ を除いてはすべて無限集合であることがわかります。ということは、$\{\pm 1\}$ は開集合ではありませんね。
であれば、(*) の左辺 $\mathbb{Z}\setminus \{\pm 1\}$ は 閉集合ではありません。

一方で、このとき、任意の $a\in \mathbb{Z}\setminus \{0\}$ に対して、$a\mathbb{Z}$ は閉集合となります。なぜならば、$a\mathbb{Z}=|a|\mathbb{Z}$ に注意すれば、

$$(a\mathbb{Z}{)}^c=(|a|\mathbb{Z}{)}^c=\bigcup _{k=1}^{|a|-1}|a|\mathbb{Z}+k$$

であり、この右辺は $a\mathbb{Z}+b$ という形をした集合の和集合になっている、すなわち $\mathcal{O}$ の元であるためです。
ということは、(*) の右辺は 閉集合の「素数個の」和集合、ということになります。

以上より、閉集合の 素数個の 和集合が閉集合でない、という状況が発生しました。
閉集合の性質 2. より、閉集合の 有限個の 和集合は 常に 閉集合です。

すなわち、素数は無限に存在しなければならないのです！

以上です。
時間と寿命が許せばあと "素数個は" 書けるんですが、今回はこれくらいにしておきます

traP アドベントカレンダー 2018、明日（61 日目）の担当は @e-suke @Sigma1023 です。