○△□

こんにちはphi16です。これはtraP AdventCalendar 12月15日の記事です。geometric shapes for higher structures の話をします。

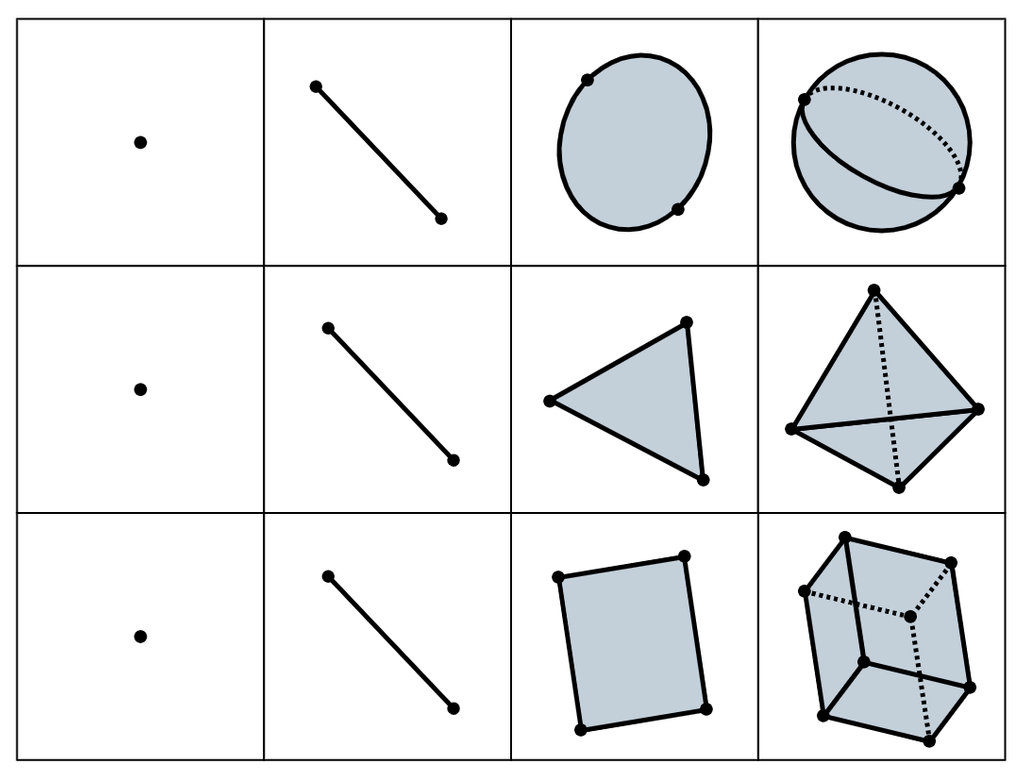
$n$ -次元物体

$n$ -次元好きですよね。 $n$ -次元の物体で最も単純なものは何でしょう。もちろん答えはありません、単純の定義が無いからです。
そんな中よく使われる「単純な $n$ -次元物体」があるので紹介します。○と△と□です。

これは2次元図形だと思うかもしれません。それは正しいです。ただこれらは自然に $n$ -次元に拡張できるという意味で扱いやすいのです。それぞれ簡単に見てみます。

$n - 1$ -次元の○を2つ集め、境界に沿って貼り合わせた内部の空間は $n$ -次元の○と同相
$n - 1$ -次元の△に新たな点を加え、各頂点との結んでできる内部の空間は $n$ -次元の△
$n - 1$ -次元の□を2つ集め、対応する2頂点達を結んでできる内部の空間は $n$ -次元の□

4次元に向かう方向も気軽に考えられますね。ところでこれらは何処に棲んでいるのでしょう。

物体は空間に棲まなければ存在しえませんが、空間に棲んでしまうと純粋な構造ではなくなります。これらの単純な $n$ -次元物体を使って他の空間を調べようとするとき、この棲んでいる空間についても考えなくてはならなくなります。それは嬉しくありません。

だから、これらの物体を空間に依存せずに、即ち幾何的ではなく代数的に定義したいのです。
というわけでそれを紹介します。

○ : globe

○の成す世界^[1]を、次で定義します。 $n$ -次元○のことを $[n]$ と表記します。

$σ_{n} : [n + 1] \to [n]$ と
$τ_{n} : [n + 1] \to [n]$ が存在し
$σ_{n - 1} \circ σ_{n} = σ_{n - 1} \circ τ_{n}$ と
$τ_{n - 1} \circ σ_{n} = τ_{n - 1} \circ τ_{n}$ を満たす

これは「 $n + 1$ -次元○から $n$ 次元○を取り出す方法が2つ存在し」「その2つから更に取り出した端点は同一である」という条件です。図を見れば成り立つことがわかるし、これを満たすなら図のように描けることもわかります。

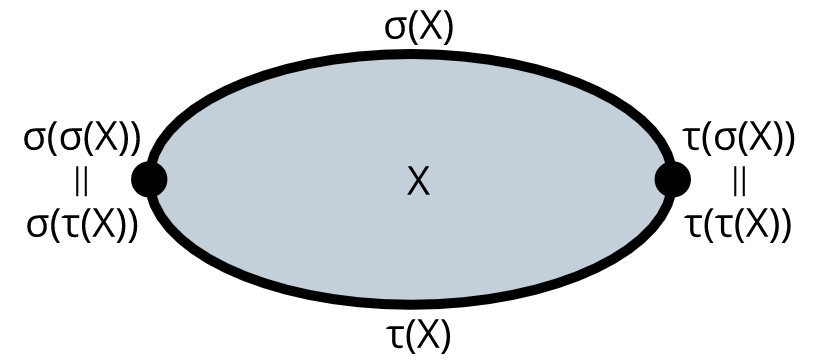
これは完全に構造的定義で、棲む空間の情報とかが一切含まれていません。だから気軽に使えて嬉しいのです。

△ : simplex

△の成す世界は次で定義されます。ここでも $n$ -次元△のことを $[n]$ を表記します。

$δ_{i}^{n} : [n] \to [n - 1] (0 \leq i < n)$ と
$σ_{i}^{n} : [n] \to [n + 1] (0 \leq i < n)$ が存在し
$δ_{i}^{n - 1} \circ δ_{j}^{n} = δ_{j - 1}^{n - 1} \circ δ_{i}^{n} (0 \leq i < j \leq n)$ と
$σ_{i}^{n + 1} \circ σ_{j}^{n} = σ_{j + 1}^{n + 1} \circ σ_{i}^{n} (0 \leq i \leq j < n)$ と
$δ_{i}^{n + 1} \circ σ_{j}^{n} = σ_{j - 1}^{n - 1} \circ δ_{i}^{n} (0 \leq i < j \leq n)$ と
$δ_{i}^{n + 1} \circ σ_{j}^{n} = i d (0 < i \leq n, i = j or i = j + 1)$ と
$δ_{i}^{n + 1} \circ σ_{j}^{n} = σ_{j}^{n - 1} \circ δ_{i - 1}^{n} (0 \leq j, j + 1 < i \leq n)$ を満たす

尚この $σ$ は○についてのものとは関係ありません。すごいごちゃごちゃしていますがやりたいことは単純で、「 $n$ 次元△から頂点を1つ削ると $n - 1$ 次元△ができる、その方法は頂点数だけある」「 $n$ 次元△の既存の頂点位置に新たな頂点を加えたことにすると潰れた $n + 1$ 次元△ができる、この方法も頂点個だけある」です。
この定義では頂点の集まりを列と見做していて、そうするとこれらの操作の間には秩序があります。例えば「複数頂点削るときはその操作順序は本質的に無関係」です。これを丁寧に記述したのが並んでいる等式で、それぞれ次の意味です。

2つの頂点を削る順序は無関係
2つの頂点を増やす順序は無関係
無関係な位置での「増やして」「削る」操作は、「削って」「増やす」のと同じ
頂点を増やしてからその増やした頂点を削るのは、何もしないのと同じ
3番目と同じ (位置関係によって添字がずれる)

だからやっていることは「列を削ったり増やす方法がまともであること」を言いたいだけです。そしてこれは△を特徴づけるものになるわけです。

○と違って△の便利なところは気軽に貼り合わせられるところでしょうか。具体的な空間について考えるときは、simplex化して空間構造を計算することが多いようです。ぐにょぐにょした空間も△で近似できますし、そういうことができる図形で最も単純 (無駄が無いという意味で) なのは△でしょう。

□ : cube

□の成す世界も同様にあるのですが、ちょっと複雑みたいです。

まず、「線分」の成す世界を考えます。これは0次元と1次元の□の成す世界です。

$i_{0} : [1] \to [0]$ と
$i_{1} : [1] \to [0]$ と
$p : [0] \to [1]$ が存在し
$i_{0} \circ p = i_{1} \circ p$ を満たす

1次元の□は線分なので、「線分には端点が2つ存在し」「同一点を結ぶ潰れた線分を考えることができ」「潰れた線分の2つの端点は同一」という意味になります。そのとおりですね。

そして、□全体の成す世界は「線分の成す世界を有限個くっつけたもの」で定義されます。くっつける、というのは情報を共存させるという意味で、 $[1]$ と $[1]$ があるとき、1次元と1次元分の情報があるので全体で2次元分の情報、即ち $[2]$ を考えることができる、みたいな感じです。

□は見た目通り、直積によってできる存在なのでそれが反映された定義であると言えます。特に $m$ -次元□と $n$ -次元□を気軽に合成して $m + n$ -次元□にできます。△でも頂点列を合成することで似たようなことは出来そうですが、□では次元がきっちり分かれてるのが嬉しいのかもしれません。

なんでこんな話を書いたのか

この辺の話は空間周りで出てくるんですが定義が難しくないですか？？？実はこの記事は「一般的な方」とは逆向きに書いてあって、多分語で調べて出てくる射の向きはすべて逆だと思います。もちろん理由としては (presheafになるから) 扱いやすいからなわけですが、そういう気持ちを一度抜いてとりあえず定義するだけ定義したいと思ったのです。つまり勉強用メモです。
というか根本的に構造だけの定義って難しいですよね。それがわかるっていうことは本質がわかるっていうことで、本質を理解するのは難しいです。
時間と知識があれば「指針としての物体」というかglobular/simplical/cubical setの話をしてみたかったです。この辺は具体的に計算するのが理解に一番早い気がしますね。

なんでこの辺を調べてるかというとcubicalttらへんからなわけですが、未だにcubeのお気持ちはわかっておりません。わかったら何か書くかもしれません。

終わりです。明日の担当は eiyaさん、spaさんです。

参考文献

ちゃんと言えば圏なわけですが ↩︎

n-次元物体