はじめまして18のshirodoniです。
今回は亀で遊んでみようと思います。
タートルグラフィックスとは
1960年代末に登場した教育用プログラミング言語「LOGO」に搭載されていた機能で、
ペンを持たせた亀に命令を出して絵を描くことができるというものです。
- 前進
- 向きを変える
ペンを上げたり色を変えたりもできるので、
様々な図形を描くことができます。
環境
Pythonにはデフォルトでタートルグラフィックス機能が付属しています。
(環境によってはグラフィックスライブラリをインストールする必要があるかもしれません)
今回使用するのはPython3です。
動作デモ
動作デモを見てみましょう。
python3 -m turtle
python3 -m turtledemo
こちらでは複数のデモを見ることができます。
亀を操る
亀の用意
まずはturtleモジュールをimportします。
from turtle import *
次にタートルオブジェクトを作成します。
kame = Turtle()
これにて準備完了です。
詳しくは公式ドキュメントを参照すると幸せになれます。
実践
肩慣らし
144度回転して前進という操作を5回繰り返してみます。
from turtle import *
kame = Turtle()
for i in range(5):
kame.right(144)
kame.forward(200)
# クリックで終了
screen = Screen()
screen.exitonclick()
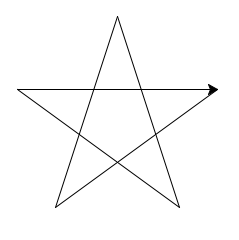
お星様ができました。
コッホ曲線を描く
再帰関数を使うと楽に描けます!
from turtle import *
kame = Turtle()
kame.speed(0)
def draw(dist, step):
if step > 0:
draw(dist / 3, step - 1)
kame.left(60)
draw(dist / 3, step - 1)
kame.right(120)
draw(dist / 3, step - 1)
kame.left(60)
draw(dist / 3, step - 1)
else:
kame.forward(dist)
draw(100, 1)
draw(100, 2)
draw(100, 3)
draw(100, 4)
screen = Screen()
screen.exitonclick()
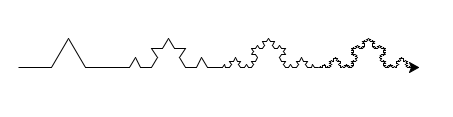
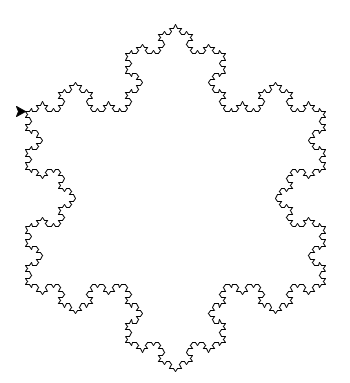
3つ組み合わせるとコッホ雪片です。
for i in range(3):
draw(300, 4)
kame.right(120)
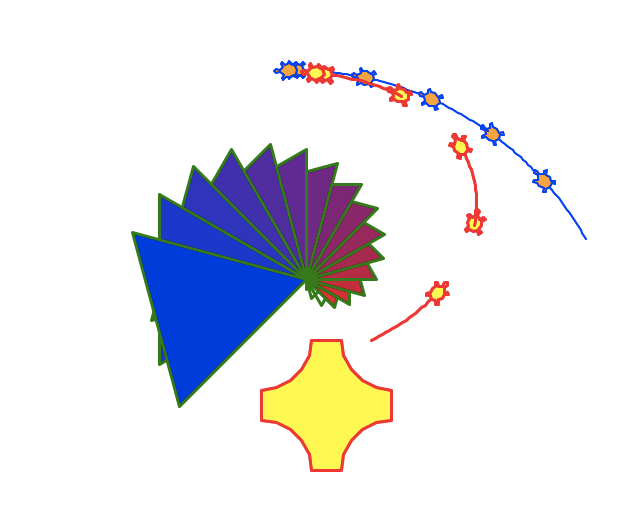
2重振り子の軌跡を描く
タートルグラフィックスの本来の用途から少しずれているような気もしますが…
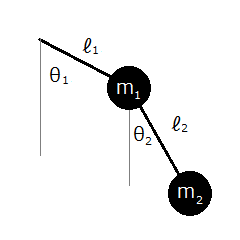
適当な初期条件で亀に上図のような2重振り子の2番目のおもりの位置を歩かせてみることにします。
2重振り子は振れ幅が大きいときに初期値を少しでも変えると軌跡が大きく変化することで有名です。これを実際に試せるようにしてみましょう。
最初に青色の軌跡を描かせて、クリックすると初期条件のを度だけずらした赤色の軌跡を描くようにしました。
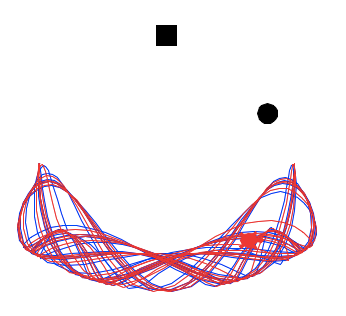
完成したプログラムはこちらです。
長いので折りたたみ
from turtle import *
from math import sin, cos, pi
import random
import time
# 質量[kg]
M1 = 1.0
M2 = 1.0
# 棒の長さ[m]
L1 = 0.5
L2 = 0.5
# 重力加速度[m/s^2]
G = 9.8
# 初期角度[rad]
R1 = random.random() * pi * 2
R2 = random.random() * pi * 2
# 初期角速度[rad/s]
V1 = 0
V2 = 0
# 1[m]に相当する長さ
pxm = 256
def bibun(r1, r2, v1, v2):
sin1 = sin(r1)
cos1 = cos(r1)
sin2 = sin(r2)
sin21 = sin(r1 - r2)
cos21 = cos(r1 - r2)
a1 = (-M2 * L1 * sin21 * cos21 * v1 * v1 - M2 * L2 * sin21 * v2 * v2 + M2 * G * sin2 * cos21 - (M1 + M2) * G * sin1) / L1 / (M1 + M2 * sin21 * sin21)
a2 = ((M1 + M2) * L1 * sin21 * v1 * v1 + M2 * L2 * sin21 * cos21 * v2 * v2 + (M1 + M2) * G * sin21 * cos1) / L2 / (M1 + M2 * sin21 * sin21)
return [v1, v2, a1, a2]
screen = Screen()
kame0 = Turtle() # 固定点
kame1 = Turtle() # おもり1
kame2 = Turtle() # おもり2
kame1.speed(0)
kame2.speed(0)
kame0.shape("square")
kame1.shape("circle")
kame2.shape("turtle")
kame1.penup()
# 軌跡の描画
def draw(r1, r2):
x1 = L1 * sin(r1) * pxm
y1 = -L1 * cos(r1) * pxm
x2 = x1 + L2 * sin(r2) * pxm
y2 = y1 - L2 * cos(r2) * pxm
kame1.goto(x1, y1)
kame2.goto(x2, y2)
# 振り子の初期化、軌跡の色変更
def init(R1, R2, V1, V2, color):
global r1, r2, v1, v2
r1, r2, v1, v2 = R1, R2, V1, V2
kame2.color(color)
kame2.penup()
draw(r1, r2)
kame2.pendown()
init(R1, R2, V1, V2, "blue")
state = 0
clicked = False
# 描画の時間間隔[s]
Wait = 1 / 30
# シミュレーションのタイムステップ[s]
Loop = 100
Step = Wait / Loop
def loop():
global r1, r2, v1, v2, clicked, state
start = time.time()
# ルンゲ・クッタ法による数値積分
for i in range(Loop):
k1v1, k1v2, k1a1, k1a2 = bibun(r1, r2, v1, v2)
k2v1, k2v2, k2a1, k2a2 = bibun(r1 + k1v1 * Step / 2, r2 + k1v2 * Step / 2, v1 + k1a1 * Step / 2, v2 + k1a2 * Step / 2)
k3v1, k3v2, k3a1, k3a2 = bibun(r1 + k2v1 * Step / 2, r2 + k2v2 * Step / 2, v1 + k2a1 * Step / 2, v2 + k2a2 * Step / 2)
k4v1, k4v2, k4a1, k4a2 = bibun(r1 + k2v1 * Step, r2 + k2v2 * Step, v1 + k2a1 * Step, v2 + k2a2 * Step)
r1 += (k1v1 + k2v1 * 2 + k3v1 * 2 + k4v1) * Step / 6
r2 += (k1v2 + k2v2 * 2 + k3v2 * 2 + k4v2) * Step / 6
v1 += (k1a1 + k2a1 * 2 + k3a1 * 2 + k4a1) * Step / 6
v2 += (k1a2 + k2a2 * 2 + k3a2 * 2 + k4a2) * Step / 6
# タートルの移動
draw(r1, r2)
if clicked:
clicked = False
# 色を変え初期条件をわずかにずらしてもう一度
if state == 0:
init(R1, R2 + 0.1 * pi / 180, V1, V2, "red")
state = 1
# 終了
elif state == 1:
screen.bye()
# 計算にかかった時間を計測して待機する時間を調整する
diff = time.time() - start
screen.ontimer(loop, max(round((Wait - diff) * 1000), 0))
def click(x, y):
global clicked
clicked = True
screen.onclick(click)
screen.ontimer(loop, 0)
screen.mainloop()
おわりに
タートルグラフィックスの強みといえば、やはりその手軽さでしょうか?
それがPythonにデフォルトで入っているということで、手軽さが極まったなあと感じます。たぶんデフォルトの機能じゃなければ私は一生これに触ることはなかったと思うので。
それでいてシンプルなコードで綺麗な図形を描けるので奥が深いです。
私にはそういったセンスがなくてつい2重振り子を作ってしまったのですが…
明日はopferさんとninjaさんの記事です。お楽しみに!
