こんにちわ。phi16です。これはtraP AdventCalendar 11月30日の記事です。

球面のおはなし

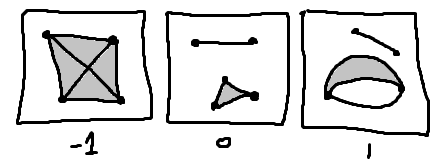
$n$ 次元球面があったとき、その「直径」を司る $n-1$ 次球面を取ることができます。

これは二次元球面 $S^2$ から一次元球面(円) $S^1$ を取ってきたということになります。

次元を上げると、 $S^3$ から $S^2$ が取れそうだということがわかります。
でも今回は、次元を下げます。

すると $S^1$ から $S^0$ が取れるということになります。0次元球面 $S^0$ ってなんですかね。
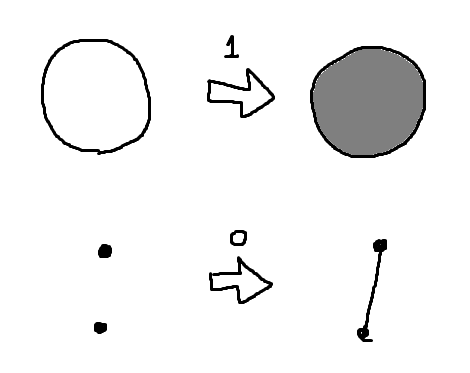
直径、という気持ちで描くとこうなります。

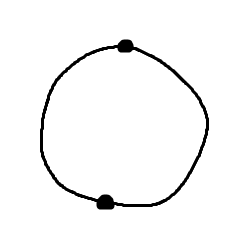
つまり $S^0$ は「二点」のことです。これは一般的な話です。

$S^0$ の各点の間に2本の線を引くと円 $S^1$ ができます。
$S^1$ に沿って2つの円板を貼ると球面 $S^2$ ができます。

今までの球面は連結だったのに、唐突に連結じゃなくなってしまうのは不思議な気がしますか？
でも実は次元を下げると別の連結性が失われていたのです。$S^2$ から $S^1$ に落とすと、単連結である性質が失われます。
これは一般化できて、$S^{n+1}$ から $S^n$ に落とすと $n$-連結性が失われます。$0$-連結のことが連結で、$1$-連結のことが単連結なのです。詳しく知りたくなったらこれでも見てください。

で、$S^2$ から $S^1$、$S^1$ から $S^0$ がわかったところで、$S^0$ から $S^{-1}$ を考えたくないですか？本来は非負の値しか考えないはずなのに、負の値のことを考えるのです。これが Negative Thinking です。

$S^2\to S^1$ においては平面が消え去ってしまいました。$S^1\to S^0$ のときは線が消えます。では、$S^0\to S^{-1}$ のときは点が消えるはずです。とすると、$S^{-1}$ は何もない空間になるのが正しそうです。次のように「次元を上げる」ことを考えてみると、正しく一般化できていそうです。

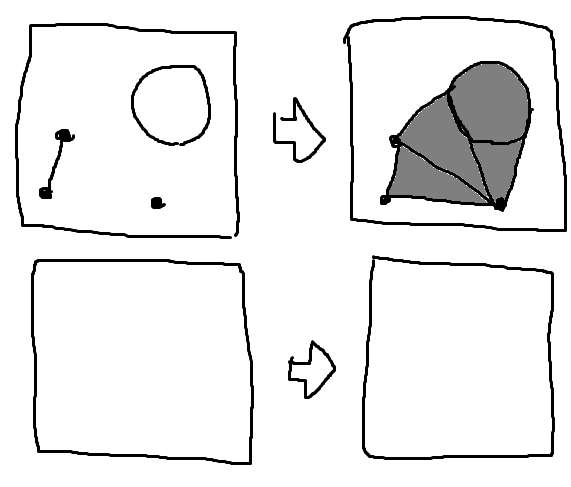
• $S^{-1}$ に2点を与え、それぞれに $S^{-1}$ の各点と結ぶ道を与える(無い)と、2点 $S^0$ ができます。
• $S^0$ に2点を与え、それぞれに $S^0$ の各点と結ぶ道を与えると、四辺でできた $S^1$ ができます。
• $S^1$ に2点を与え、それぞれに $S^1$ の各点と結ぶ道を与えると、円錐が2つくっついてできる $S^2$ ができます。

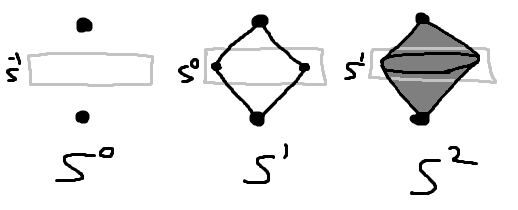
これはこれでうまくいくものなのです。

自然数を $-1$ から始めたくなりません？

空間のおはなし

さて、ところで空間には次元の概念が(だいたい)あります。私たちは通常3次元空間で生活しているわけですが、「空間の次元を潰す」ということをちょっとしてみたいのですね。ここで「潰す」というのは「その次元の存在を自明にする」という意味です。むずかしいね。

私たちはなんとなく空間そのものの構造を考えているんですが、つながっている領域をふわーっと泳げたりするのは自明であるとみなします。つまり中身が詰まっているところはみんな同じ点としてしまうのです。そうすると空間の広さみたいな情報が消え去って、純粋な「つながり」だけを取り出すことができます。何かを自明にするというのは空間構造の本質を調べるためのよくある考え方です。

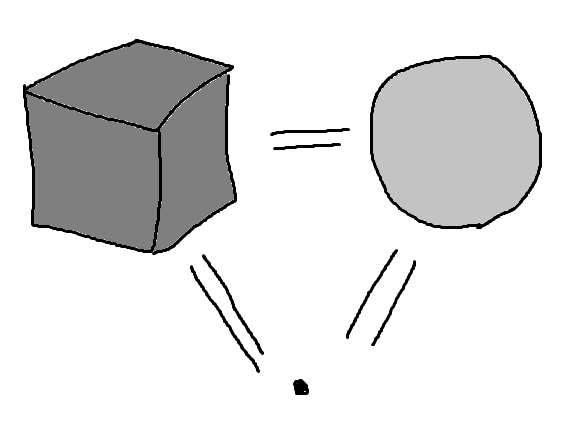
じゃあ殆どの空間は同じじゃないのか、って思うんですけど、そうでもないんです。その例が円 $S^1$ やトーラス $T^2$ です。こいつらは詰まっている部分をいくら縮めても穴が残ってしまうため自明にはできないのです。ちなみにドーナツは $S^1$ と同じ空間です、中身が詰まっているので。

で、この辺の話は別にホモトピー論を読めばいいんですが、私は Negative Thinking したいんです。

以上の「自明」の気持ちの元では、 $n$ 次元構造というのは実質的に $n$ 次元球面の存在を言っています。ならば $n$ 次元構造を潰すためには $n$ 次元球面を埋めちゃえばいいんです。$S^2$ の2次元構造を潰すと中身の詰まった球となり、点になります。$S^1$ の1次元構造を潰すと円板になり、点になります。ちなみにトーラスには2次元構造は無いことになります。むずかしい。

1次元構造を潰すと世界は点のみになりました。では0次元構造を潰すと何ができるでしょうか？

やることは同じです。$S^0$ の0次元構造を潰せばいいのです。「$S^0$ の中身を埋める」というのは、$S^0$ の各点を線でつないで自明な空間にする、という意味です。「複数の点からなる空間」における $S^0$ の存在は「任意の2点」そのものです。よって、これを自明にするということは全ての点を1つにつなぐということを意味します。

その結果、$0$ 次元構造が潰された空間というのは「点がある」という情報しか持ちません。もともと点が一個もない空間は潰しても点はありませんが、点が1つでもある空間は「点があった」ことだけを残して情報が消え去ってしまうのです。

結果できた空間は、$-1$ 次元構造からなる空間ですね。$-1$ 次元というのは「あるか」「ないか」を表す構造とも言えそうです。$0$ 次元のときは点の区別・点の数の情報があったのにだいぶ世界が潰れちゃいましたね。

では $-1$ 次元構造を潰しましょう。$S^{-1}$ は何も無い空間のことでした。これを一点に潰すということは、何も無いところにも点を生成するという意味です。意味的にも「あるかないか」の区別を無くすということで、情報が完全に消え去った世界が完成しそうです。

というわけでできた $-2$ 次元構造からなる空間は、「一点」そのもの以外の何者でもありません。情報はついに消え去ってしまいました。かなしいね。

では逆に。$-2$ 次元の世界から元に戻ってみましょう。「点と点の関係が $n-1$ 次元の空間を $n$ 次元の空間とする」という気持ちです。

点と点の関係が $-2$ 次元、つまり常に自明だとしましょう。これはその2つの点が全く等しいことを示しています。つまり「全ての点は等しい」。これには「1点のみある」場合と「点が無い」場合の2通りがあります。これが $-1$ 次元でした。

点と点の関係が $-1$ 次元、つまり自明か無いかの2通りだとしましょう。自明であるような点たちは推移的にくっついて、1つの点になります。もともと無関係な点はそのまま残ることでしょう。すなわち「点たちが散在している状況」です。これが $0$ 次元です。

点と点の関係が $0$ 次元、つまり点と点の間には複数の「等しい」という関係があるとしましょう。2つの点の間に異なる「等しい」という関係があったとき、それはまさしく円 $S^1$ を成します。これによって自然に線の構造が復元され、$1$ 次元を取り戻しました。

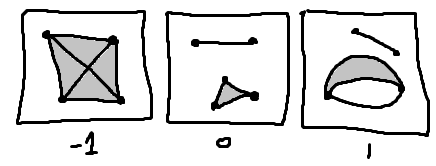
点と点の関係が $1$ 次元の場合も同様に、また $S^2$ が自然に構成されますが、これらの話は前半の球面のおはなしで行った議論と類似していることがわかることでしょう。

自然数を $-2$ から・・・

おわりに

まぁ特に意味なさそうな話をしているわけですが、案外そうでもないんです。
$-1$ 次元の世界というのはまさしく真偽値のモデルで、この上で古典論理を動かすことができます。でも逆に言えばその上に $0$ 次元、$1$ 次元…と世界を連ねることができるのです。

真と偽しかない世界よりももっと広い世界を見たくないですか？

特にオチはないです。Impressiveだと感じてくれたらうれしいです。あと私は直観主義論理が好きです。

参考文献

• negative thinking in nlab 元ネタです。
• Homotopy Type Theory HoTT Bookの Truncations (7.3章) が後編の元ネタです。まぁ近い話がnlabにも書いてあります。
• n-connected space in nlab $n$-connectedの話です。$(-2)$-connectedも出てきます。

なおこれはおもしろい話があるので紹介しましたという記事です。

明日は@tako, @yasu, @Double_oxygenNさんたちの記事です。ついに12月ですね。