この記事はtraP Advent Calendar 11月22日の記事です。
こんにちは、ninjaです。ハル研究所プログラミングコンテスト2017で4位になりました✌
今回はぷよぷよを計算機の力でプレイしていきます。
0. ぷよぷよとは
ぷよぷよは対戦型パズルゲームです。
降ってくる3~5種類のピース(ぷよ)を操作して最上部に来ないようにするゲームです。
ぷよは4つ以上つながると消え、消した量に応じて相手を妨害することができます。
ぷよが消えたあとにさらにぷよがつながり、消えることを連鎖といいます。
残念ながら対戦する相手がいなかったのでとことんぷよぷよという一人プレイ用のモードで連鎖数を伸ばす遊びをします。
1. 準備
全てシミュレーションしてもよかったのですが、画面映えしなさそうだったので実機で行うことにしました。
使ったもの
- PCに映すぷよぷよ
- PS2
- ぷよぷよフィーバー
- GV-USB2
- アマレコTV
画面からぷよの色を取得する
windows apiでPS2のキャプチャーのウィンドウのピクセル情報をもらい、その色からぷよが何色かを取得します。
各ぷよに関して5点から色を取得し、その平均値からRGBの3次元ベクトルを作成します。
ぷよの赤緑青黄の値を計測して大体
ターン遷移検出
次のターンに移る際、0.2秒程度ぷよがスライドすることによって背景の色がぷよの色として得られます。
プログラム側ではこの色を見ることで、ターンの遷移を検出することができます。
ターンの遷移と色の取得ができたのでいよいよ探索部分の構築をします.
2. アルゴリズム
ここで今回のゲームのルールを決めます。
- とことんのオリジナル(中辛)
- 連鎖が起こった時点で終了
- 各ターン2手先までを入力とし、出力を手動で配置
- ポーズを使用しない(探索時間は自由落下時間依存)
入力は2手のみなので全探査は簡単に行うことができます。
しかし、2手先程度ではどの操作がよいのか判定することは非常に難しいです。
そこで、モンテカルロ木探索[2]を行います。
乱数で後続のぷよを上限まで生成し、その中での最適な第一ぷよに対する操作を求めます。
今回は5回行い、多数決を取り、操作を決定します。
複数の乱数入力で同じ初手になるということは、現在見ることができない先の入力がどのようなものであってもある程度有効に働くと考えることができるためです。
後続のぷよがすべて明らかなとき、プレイヤーが行うことができる操作は1手につき22種類です(縦2種類*6 + 横2種類*5)
なので被りを考慮しなければ、n回先の盤面状態は22^nあると考えられます。
全ての状態を見て、その中で一番連鎖数の多いものを採用できればよいのですが、nが6を超えるあたりから全探査は困難になります。
ですが、この盤面の中には明らかに大きい連鎖数を達成できないものがたくさんあります。

適当においたものです。
このような盤面を無視することができれば、大きい連鎖数を見つけやすくなります。
盤面に対して、大きい連鎖数を作ることができるか、という指標に評価関数を導入します。
さらに、探索にビームサーチ[3]を導入します。
ビームサーチは各ターンの状態を評価関数が大きい順に固定数(ビーム幅と言う)で採用していきます。
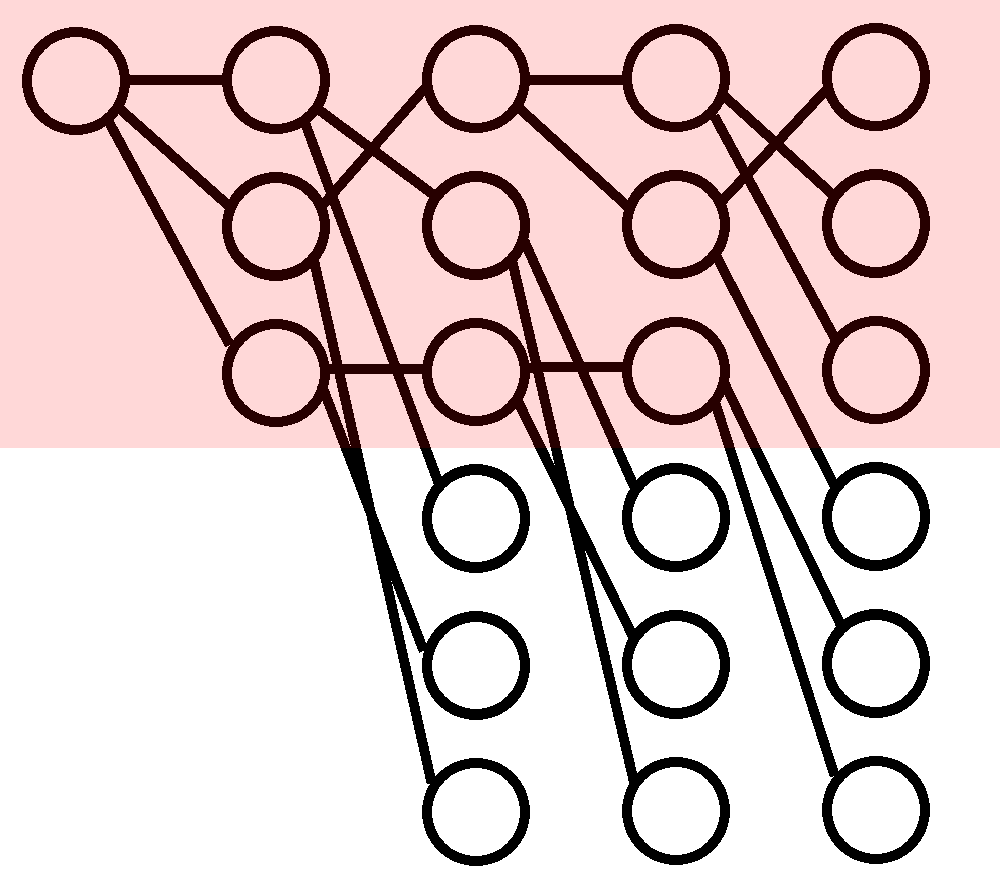
幅3のビームサーチ[4]
よい探索が行えるかはほぼ評価関数の質で決まるので後は評価関数を頑張って生成します。
3. 実演
今回は以下の条件で探索を行いました。
ビーム幅: 50
モンテカルロ木探索: 5回
1
評価関数:
隣接する同色の数^2の総和
2
評価関数:
隣接する同色の数^2の総和+0, 5列の高さ*2+1, 4列の高さ
3
評価関数:
隣接する同色の数^2の総和+0, 5列の高さ*2+1, 4列の高さ
+各列に1つだけぷよを落としたときに連鎖する数の最大値*10
4
評価関数:
隣接する同色の数^2の総和+0, 5列の高さ*2+1, 4列の高さ
+4または5個で消える連鎖数の最大値*10
4. おわりに
最後まで読んでいただきありがとうございました。
思い付きの実装が多かったのですがいい感じになったので助かりました。
マラソン系で結果を残せるようになりたいなあと思うばかりです。
明日はarcusさん、crotkazさんの2人です。
参考文献
MSDN
スクリーンキャプチャ【Windowsプログラミング研究所】
プログラミングと色々 ほかのプログラムのウィンドウハンドルを取得する
ぷよぷよAIの新しい探索法
[1]:
PS2の映像出力はアナログで、画面にノイズがたくさん入ってました。
緑と黄が色的に近かったのでそこの判定が一番困った点でした。
[2]:
囲碁や将棋のAIなどで使われているようです。乱択は神。
[3]:
去年のハルコンではかなり有効な手段だったので、今年も使うぞと意気込んでいたのですが結局使いませんでした。
[4]:
ビーム幅1だと貪欲法、十分に大きい値だと全探索になります。
