「シェーダに興味はあるけど敷居が高い」との声が私の周りでちらほらと囁かれ始めたのでこんな記事を書いてみます。
まずは普通の話
ここを開いてください。英語のサイトでビビるかもしれませんが、そこはなんとか耐えていただき、右上の「New Shader」を押してください。
下のようになるかと思います。
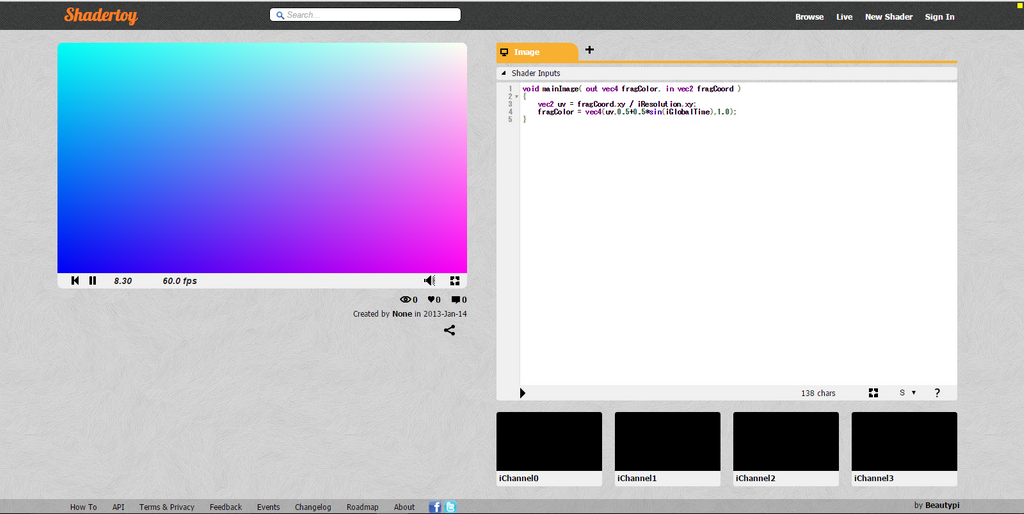
左側がグラデーションがシェーダで描かれた画像、右側がソースコードになります。開いた時点でデフォルトのシェーダが書かれておりますので、まずはその説明から入ります。
今回シェーダと呼ぶものは、一般にはピクセルシェーダ、またはフラグメントシェーダと呼ばれるもので、「座標を引数としてその座標の色(RGBAを持った4次元ベクトル)を返す関数を書く」ことを目的とするものです。ShaderToyで書くときは、メイン関数として1行目に宣言されているmainImage関数がそれにあたるもので、ここからプログラムは開始します。
ここでシェーダを書くために使う言語はGLSL(OpenGL Shader Language)と呼ばれるもので、デフォルトのコードを見てもお分かりになるかと思いますが、基本的な文法はかなりC言語に似通っています。mainImageを見てみると、「返り値がvoid型で引数にvec4型のfragColorとvec2型のfragCoordを取る関数」であることがわかるかと思います。inとoutはそこまで気にしなくてよいです。要するにfragCoordとかを使ってfragColorにうまい具合に値を入れてやることが目的です。そして、fragCoordが「今から色を決めようとしているピクセルの座標(左下原点)」で、fragColorが「xyzw成分にそれぞれそのピクセルのRGBA成分をもったベクトル」です。
mainImageの中を見てみますと、
vec2 uv = fragCoord.xy / iResolution.xy;
となっているかと思います。fragCoordはmainImageの引数でしたが、iResolutionとか何でしょうか?そう思った方は(そう思わなくても)ソースコードの上にある「Shader Inputs」のところをクリックしてみてください。
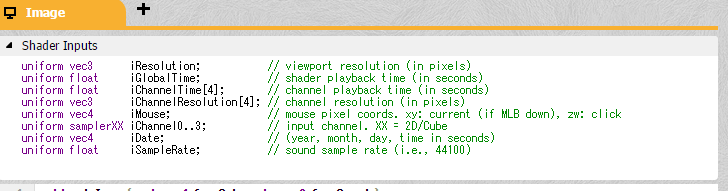
こんなふうになりましたか?ここにはuniformとついた何やら変数らしきものが宣言しまくってあります。uniformは、「外部の情報がここに入ってきますよ」という意味です。つまり、iResolutionとかiGlobalTimeとかいう変数はデフォルトで宣言されていて、自動的に中身が入ってきてくれているのです。ちなみに、iResolutionは「描画領域の幅と高さをxy成分にもった2次元ベクトル」で、iGlobalTimeは「シェーダが起動してから何秒経ったか」です。それを踏まえたうえでもう一度先ほどのコードを読んでみますと、「いま注目している座標のxy成分を描画領域の幅と高さで割ったものをuvという変数に代入」ということになります。数学をやっている方は、「ベクトル÷ベクトル?」とか思うかもしれませんが、GLSLではこの文法が通用します。意味は、単純に各成分どうしを割り算するという意味です。
さて、このようにして得られた2次元ベクトルuvが何を意味しているかというと、ズバリ「描画領域の幅と高さを両方1としたときの注目ピクセルの座標」です。この方があとあと計算が楽になるので、一度fragCoordをuvに変換したわけですね。
次の行は
fragColor = vec4(uv,0.5+0.5*sin(iGlobalTime),1.0);
となっていると思います。ここでfragColorへの代入、すなわちそのピクセルの色を決定しているわけです。ですが、何やら面倒なことが色々と書いてあるようですので、一旦もっとシンプルな形に直しましょう。
fragColor = vec4(uv,1.0,1.0);
こんなかんじにしてみて、ソースコード左下の▶ボタンをクリックしてください。
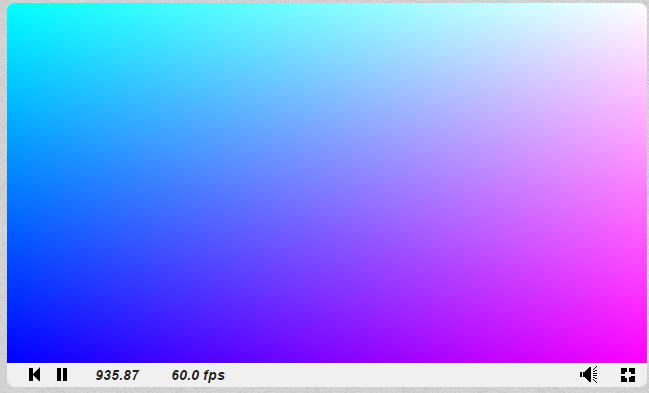
こんなかんじになりましたか?エラーが出ている方は、「1.0」を「1」にしていないか確認してみてください。GLSLはお馬鹿さんなので、「1」と表記するとそれをint型と認識してしまい、型が違う(vec4の成分はfloat型)のでコンパイルエラーにされてしまいます。
まず画面の一番左下のところを見てみると、真っ青になっています。これは、RGBで書くと、(0,0,1)ということになります(GLSLではRGBの上限値を1とします)。一番左下のピクセルの色を決定するとき、fragCoordは(0,0)になっていますから、当然uvも(0,0)になります。すると、fragColorに代入される値は(0,0,1,1)となります。最後の値はとりあえず1にしときゃいいみたいなかんじなので、RGBは(0,0,1)です。
右上を描画しようとすると、今度はuvが(1,1)になりますので、RGBは(1,1,1)となり、真っ白になります。同様に、左上、右下で考えてみると、RGBが(0,1,1)で水色、(1,0,1)で紫になります。いまは角についてのみ考えましたが、その間のところではuvのx,y成分が0~1の範囲で滑らかに変化していくので、このように綺麗なグラデーションが描かれます。
ここまでお分かりになりましたら、fragColorの式をもとに戻してみましょう。その式は、先ほどの式のBlue成分だけを
0.5+0.5*sin(iGlobalTime)
にしたものです。sinは言わずと知れた三角関数のアイツです。iGlobalTimeは経過時間なので、sin(iGlobalTime)は時間経過にしたがって-1~1の間を滑らかに揺れます。sinの値域は-1~1なので、それに0.5掛けて範囲を-0.5~0.5に直し、0.5足すことで範囲を0~1にしています。GLSLにおいて、RGBを0より小さくしたり1より大きくしたりすると、無理やり0~1の範囲に押し込められてしまうため、範囲を0~1になおしてあげていたのです。これによって、RG成分は座標によって、B成分は時間によってなめらかに0~1の範囲を動くことになり、最初のシェーダが出来上がっていました。こんなシェーダでも、工夫次第で色々と改造はできます。例えば、
fragColor = vec4(0.5+0.5*sin(iGlobalTime), uv,1.0);
としたり
fragColor = vec4(0.5+0.5*cos(iGlobalTime), uv.y,0.5+0.5*sin(iGlobalTime),1.0);
としたりしてみれば、それはそれでまた違ったものが見られます。また、画像を使うこともできますので、†ちょっと†いじると

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord.xy / iResolution.xy - .5;
float t = clamp(1. - length(uv) * 3., 0.0, 1.0) * 3.;
vec2 uv2 = vec2(uv.x * cos(t) - uv.y * sin(t), uv.y * cos(t) + uv.x * sin(t));
fragColor = texture2D(iChannel0, uv2);
}
こんなかんじに渦巻きにしたりもたった数行でできます。
ここまでがシェーダの基礎です。次回からは、本来のシェーダの役割から逸脱した「レイマーチング」と「距離関数」と呼ばれるものを合わせた変態技術を紹介してきます。ちなみにShaderToyのすごい作品群はだいたいこの技術を使っています。
