はじめに

この記事はアドベントカレンダー2025 16日目の記事です

コンテスト中の人へ or 結果が早く知りたい人へ

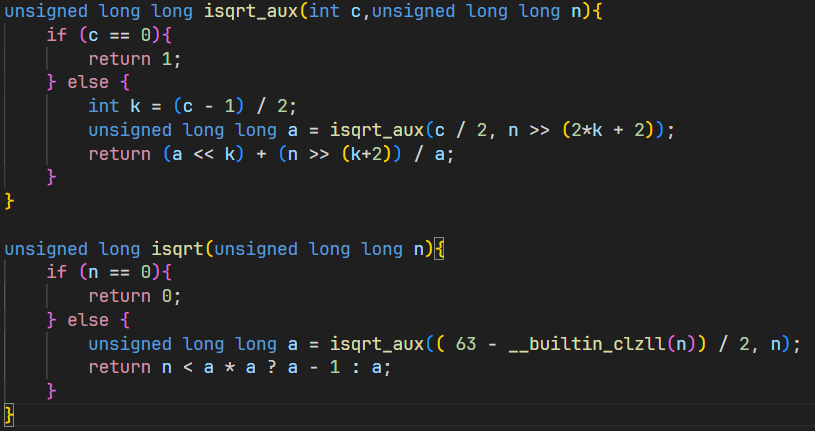
コードを示します。コードテストでも何でもにこれをコピペしたら、正しく動いていることが分かると思います。

#include <iostream>
#include <vector>

using namespace std;

unsigned long long isqrt_aux(int c,unsigned long long n){
    if (c == 0){
        return 1;
    } else {
        int k = (c - 1) / 2;
        unsigned long long a = isqrt_aux(c / 2, n >> (2*k + 2));
        return (a << k) + (n >> (k+2)) / a;
    }
}

unsigned long isqrt(unsigned long long n){
    if (n == 0){
        return 0;
    } else {
        unsigned long long a = isqrt_aux(( 63 - __builtin_clzll(n)) / 2, n);
        return n <= a * a - 1 ? a - 1 : a;
    }
}

// ===========================================

int main(){
    vector<unsigned long long> sample{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,100,1000,1024,314159265,4611686018427387903ULL,4611686018427387904ULL,18446744073709551614ULL,18446744073709551615ULL};
    for (int i=0;i < sample.size();i++){
        unsigned long long s,ss;
        s = sample[i];
        ss = isqrt(sample[i]);
        cout << s << " -> " << ss << "\n";
    }
}

導入

最近Pythonからc++に移行しようと頑張っているn3です。ADTでABC397のD問題をc++で解こうとしたときに、isqrtが必要になったので自作してみました。

isqrt(n) という、$\text{isqrt}(n)=\lfloor \sqrt{n}\rfloor$ という関数、$\sqrt{n}$ 以下の最大の整数を返す関数があります。例えば、

$$\text{isqrt}(5)=\lfloor \sqrt{5}\rfloor =\lfloor \mathrm{2.23...}\rfloor =2$$

$$\text{isqrt}(42)=\lfloor \sqrt{42}\rfloor =\lfloor \mathrm{6.48...}\rfloor =6$$

$$\text{isqrt}(100)=\lfloor \sqrt{100}\rfloor =\lfloor 10\rfloor =10$$

みたいな関数です。この関数があると、ある数以下の平方数の数え上げや、ある数が平方数かの判定が行えます。
Pythonにはisqrtが組み込み関数で存在するのですが、c++にはisqrtに相当するものは無いので、自分で書く必要があります。二分探索で $O(\log N)$ のコードを書いても良いのですが、Pythonのisqrtはニュートン法を用いて実装されていて、$O(\log \log N)$ で求めることができます。

$O(\log \log N)$ ですよ！速くないですか？！今回はその内部実装とそのコードの正当性の証明を解説します。

使用例

解説の前に、実際にこのコードが正しく動いていることを確認してみましょう。

ニュートン法について

詳細はこのブログを読みましょう^[1]：https://trap.jp/post/890/

要点だけをまとめると、ある関数 $f(x)=0$ の解を求めるときに、適当な初期値 $x_0$ を用いて、

$$x_{n+1}=x_n-\frac{f^{\prime }(x_n)}{f(x_n)}$$

という漸化式における、 ${\lim }_{n\to \infty }{x}_n$ が $f(x)=0$ の解に収束するというものです。

証明の概要

上のコードを見ると、2つの関数 isqrt_aux(c,n) と isqrt(n) を用いています。isqrt(n) の方は後で解説するとして、主題はisqrt_aux(c,n)です。
こいつは、

$$(a-1{)}^2<n<(a+1{)}^2$$

となるような$a$を返します。要するにisqrt_aux(c,n)は、$\lfloor \sqrt{n}\rfloor ,\lfloor \sqrt{n}\rfloor +1$ のいずれか一方を返します。そのため、isqrtの方で適切に確認すれば、求めたい$\lfloor n\rfloor$ の値を得ます。

isqrt_aux(c,n)は自身を再帰的に呼び出すことで近似値を計算します。
具体的には、与えられた数の上半分を切り出したそのisqrtの近似値に関して、それを初期値としてニュートン法を行って近似値を計算すると言った感じです。言葉だと分かりにくいので、具体的にやってみましょう。(雰囲気だけですが)^[2]

$\text{isqrt}(69380570)=\lfloor \sqrt{69380570}\rfloor$ を求めてみます。

• $69380570$ のisqrtを求めたい
  • 全体の上4桁の $6938$ のisqrtを求めたい
    • 全体の上2桁の $69$ のisqrtを求めたい
    • これは明らかに、$\text{isqrt}(69)=8$である。
  • $\text{isqrt}(69)=8$ なら、引数を100倍して $\text{isqrt}(6900)\approx 80$である
  • 初期値 $80$、$f(x)=x^2-6938$ でニュートン法を一回行うと、$x=83.36\cdots$となる。切り捨てて $\text{isqrt}(6938)\approx 83$ とする。
• $\text{isqrt}(6938)\approx 83$ なので、引数を10000倍して $\text{isqrt}(69380000)\approx 8300$ である
• 初期値 $8300$、$f(x)=x^2-69380570$ でニュートン法を一回行うと、$x=8329.55\cdots$となる。切り捨てて $\text{isqrt}(69380570)\approx 8329$ とする。

こうして得られた、$\text{isqrt}(69380570)\approx 8329$に関して、

$$8329^2=69372241\le 69380570<69388900=8330^2$$

が成り立つので、求める値は $\text{isqrt}(69380570)=8329$ である。

このようにすることで、isqrtを適切に近似することができます。上の例はあくまで適当な数値なので常に正しい答えが返ってくるとは限りませんが、Pythonのisqrtは、厳密に誤差評価をすることで必ず妥当な答えが帰ってくることを証明できます。

補題

補題1

任意の実数 $x$,整数 $n,a,b$ に関して、以下が成り立つ。

$$\lfloor n+x\rfloor =n+\lfloor x\rfloor$$

$$x-1<\lfloor x\rfloor \le x$$

$$\lfloor \frac{\lfloor x/a\rfloor }{b}\rfloor =\lfloor \frac{x}{ab}\rfloor$$

$$\lfloor x\rfloor =\lfloor \frac{x}{2}\rfloor +\lfloor \frac{x+1}{2}\rfloor$$

補題2

63 - __builtin_clzll(n) は n を二進数で表したときの桁数から1引いたもの、つまり $\lfloor {\log }_{2}n\rfloor$ となる。

補足：__builtin_clzll(n)は、ある数を符号なし64bit2進数で表した場合に、「1になっている最も左にあるビット」より左に0になっているビットが何個あるかを数える関数です。

補題3

補題1の3番目の式と補題2より、以下が従う

$$\lfloor \lfloor {\log }_{2}n\rfloor /2\rfloor =\lfloor \frac{{\log }_{2}n}{2}\rfloor =\lfloor {\log }_{4}n\rfloor$$

補題4

$f(x)=x^2-a$ にニュートン法を用いるときの漸化式は、

$$x_{n+1}=\frac{1}{2}\left(x_n+\frac{a}{x_n}\right)$$

となる。

定理

ここからは、適宜コードを見ながら理解する必要があるので、再掲しておきます。

unsigned long long isqrt_aux(int c,unsigned long long n){
    if (c == 0){
        return 1;
    } else {
        int k = (c - 1) / 2;
        unsigned long long a = isqrt_aux(c / 2, n >> (2*k + 2));
        return (a << k) + (n >> (k+2)) / a;
    }
}

unsigned long isqrt(unsigned long long n){
    if (n == 0){
        return 0;
    } else {
        unsigned long long a = isqrt_aux(( 63 - __builtin_clzll(n)) / 2, n);
        return n <= a * a - 1 ? a - 1 : a;
    }
}

定理1

コード中のisqrt_aux(c,n) の c は、 $\lfloor {\log }_{4}n\rfloor$ となる。

証明

isqrt(unsigned long long n)で現れる場合(BaseCase)：
isqrt(n) のコードの中にある、isqrt_aux(( 63 - __builtin_clzll(n)) / 2, n); に着目する。補題2,3より、( 63 - __builtin_clzll(n)) / 2は $\lfloor {\log }_{4}n\rfloor$ であるので、この場合示された。

isqrt_aux(int c,unsigned long long n)で現れる場合：
扱いやすさのため、このスコープ内で新たに定義される変数に ${}^{\prime }$ を付ける。引数として与えられる $n,c$ には付けていない。

$$k^{\prime }=\lfloor (c-1)/2\rfloor$$

$$c^{\prime }=\lfloor c/2\rfloor$$

$$n^{\prime }=\lfloor n/2^{2k^{\prime }+2}\rfloor$$

ここで、$c=\lfloor {\log }_{4}n\rfloor$ であるならば、 $c^{\prime }=\lfloor {\log }_4{n}^{\prime }\rfloor$ であることを示せば、帰納的に示される。

ここで、補題1の式4より、

$$c=\lfloor \frac{c}{2}\rfloor +\lfloor \frac{c+1}{2}\rfloor$$

$$=\lfloor \frac{c}{2}\rfloor +\lfloor \frac{c-1}{2}\rfloor +1$$

$$=c^{\prime }+k^{\prime }+1$$

つまり、

$$c=c^{\prime }+k^{\prime }+1\cdots (1)$$

また、

$$\lfloor {\log }_4{n}^{\prime }\rfloor =\lfloor {\log }_4(n/2^{2^{\prime }k+2})\rfloor$$

$$=\lfloor {\log }_{4}n-(k^{\prime }+1)\rfloor$$

$$=\lfloor {\log }_{4}n\rfloor -(k^{\prime }+1)$$

つまり、

$$\lfloor {\log }_{4}n\rfloor =\lfloor {\log }_4{n}^{\prime }\rfloor +k^{\prime }+1\cdots (2)$$

$(1)$式と$(2)$式を、帰納法の仮定 $c=\lfloor {\log }_{4}n\rfloor$ に代入して、

$$c^{\prime }+k^{\prime }+1=\lfloor {\log }_4{n}^{\prime }\rfloor +k^{\prime }+1$$

$$⟺c^{\prime }=\lfloor {\log }_4{n}^{\prime }\rfloor$$

よって、帰納法により、題意は示された。

定理2

$n>0$ とする。isqrt_aux(c,n)の返り値を $a$ としたとき、

$$(a-1{)}^2<n<(a+1{)}^2\cdots (3)$$

となる。

コードの解説

再帰的に、$\text{isqrt}(n/2^{2k^{\prime }+2})$ の近似値 $a$ が 式$(3)$ を満たすとしたとき、$\text{isqrt}(n)$ の近似値を $a\cdot 2^{k^{\prime }+1}$ として、ニュートン法の式

$$\frac{1}{2}\left(a\cdot 2^{k^{\prime }+1}+\frac{n}{a\cdot 2^{k^{\prime }+1}}\right)$$

$$=a\cdot 2^{k^{\prime }}+\frac{n}{a\cdot 2^{k^{\prime }+2}}$$

に代入し、これがまた 式$(3)$ を満たす十分な近似になっているので、これを返している

証明

帰納的に示す。引数の $c=\lfloor {\log }_{4}n\rfloor$ が $0$ になるとき、つまり $n=1,2,3$ のとき、引数の $c$ は ${\log }_{4}n=0$ となり、コード中のif文より $1$ を返す。 これは明らかに式(3)を満たす。

$c>0$ のときに成り立つことを、$c$以下の自然数 $c^{\prime }(<c)$ で式(3)が成り立つことを仮定して示す。
これは再帰的に isqrt_aux() が呼ばれ、この返り値 $a$ として、

$$(a-1{)}^2<\frac{n}{2^{2k^{\prime }+2}}<(a+1{)}^2\cdots (4)$$

となる。^[3]

これは、分母を払ってルートを取れば、

$$-2^{k^{\prime }+1}<a\cdot 2^{k^{\prime }+1}-\sqrt{n}<2^{k^{\prime }+1}\cdots (5)$$

となる。

ここで、下記の $e$ をこの $a$ を用いて、

$$e=a\cdot 2^{k^{\prime }}+\frac{n}{a\cdot 2^{k^{\prime }+2}}$$

と定義したとき、

$$e-\sqrt{n}=a\cdot 2^{k^{\prime }}+\frac{n}{a\cdot 2^{k^{\prime }+2}}-\sqrt{n}$$

$$=a\cdot 2^{k^{\prime }}+\frac{n}{a\cdot 2^{k^{\prime }+2}}-\sqrt{n}$$

$$=\frac{a^2\cdot 2^{2k^{\prime }+2}+n-a\cdot 2^{k^{\prime }+2}\sqrt{n}}{a\cdot 2^{k^{\prime }+2}}$$

$$=\frac{(a\cdot 2^{k^{\prime }+1}-\sqrt{n}{)}^2}{a\cdot 2^{k^{\prime }+2}}$$

よって、$0\le e-\sqrt{n}$ であり、また $(5)$式 より、

$$d-\sqrt{n}<\frac{(a\cdot 2^{k^{\prime }+1}-\sqrt{n}{)}^2}{a\cdot 2^{k^{\prime }+2}}<\frac{(2^{k^{\prime }+1}{)}^2}{a\cdot 2^{k^{\prime }+2}}$$

$$=\frac{(2^{k^{\prime }+1}{)}^2}{a\cdot 2^{k^{\prime }+2}}$$

$$=\frac{2^{k^{\prime }}}{a}$$

ここで、$a$ に関する $n$ を用いた評価を得る必要がある。

定理1より $c=\lfloor {\log }_{4}n\rfloor$、また、 $k^{\prime }=\lfloor (c-1)/2\rfloor$ なので、

$$2^{2k^{\prime }+1}\le 2^{2\cdot \lfloor (c-1)/2+1\rfloor }$$

$$=2^c\le \sqrt{n}$$

よって最左辺/最右辺より、

$$2^{2k^{\prime }+1}\le \sqrt{n}$$

また、$(4)$式より、

$$\sqrt{n}<(a+1)\cdot 2^{k^{\prime }+1}$$

よって、

$$2^{k^{\prime }}<a+1$$

$$⟺2^{k^{\prime }}<=a$$

以上より、 $0\le d-\sqrt{n}<2^{k^{\prime }}/a\le 1$ なので、

$$\sqrt{n}\le d<\sqrt{n}+1$$

ここで、$e=\lfloor d\rfloor$ とすると、補題1の2番目の式より、

$$\sqrt{n}-1<e<\sqrt{n}+1$$

$$⟺(e-1{)}^2<n<(e+1{)}^2$$

よって、返り値としてこれを返すことで、$(3)$式を満たす。

帰納法より題意は示された。

補足

これらより、先に示したisqrt(n)が正しく動作していることが分かります。

isqrt部分の抜粋

unsigned long isqrt(unsigned long long n){
    if (n == 0){
        return 0;
    } else {
        unsigned long long a = isqrt_aux(( 63 - __builtin_clzll(n)) / 2, n);
        return n <= a * a - 1 ? a - 1 : a;
    }
}

$n=0$ のときは別で処理して、$n>0$の場合はisqrt_auxが $a=\lfloor \sqrt{n}\rfloor ,\lfloor \sqrt{n}\rfloor +1$ を返すので、どちらが正しいかを場合分けします。
$n<a^2$ のとき、これは $\lfloor \sqrt{n}\rfloor$ の満たすべき不等式

$$\lfloor \sqrt{n}{\rfloor }^2\le n<(\lfloor \sqrt{n}\rfloor +1{)}^2$$

に反しているので、$-1$する必要があります。この処理は三項演算子を使ってシンプルに、n <= a * a - 1 ? a - 1 : aと書くことが出来ます。ここで、n <= a*a-1と <=で判定しているのは、a*a-1とすることで unsigned long long でオーバーフローしないようにするためです。$a$は最大で $2^{32}$なので、そのままn < a*aのように2乗すると0になっておかしくなります。そこでこのように計算しています。

実行速度

AtCoderのコードテストで、速度比較をします。
測定項目として、

• $[1,10^8)$ の連続値
• $[10^{12},10^{12}+10^8)$ の連続値
• $[1,10^9)$ の乱数 $10^8$ 個
• $[10^{12},2\times 10^{12})$ の乱数 $10^8$ 個

を採用しました。どれも $10^8$ の計算をしています。

#include <iostream>
#include <vector>
#include <algorithm>
#include <chrono>
#include <random> // 乱数生成用
#include <iomanip>
#include <cmath>

using namespace std::chrono;
using namespace std;

#define ll long long

// ===========================================
// 再帰 + ビット演算版 (Recursive Bitwise)
// ===========================================
unsigned long long isqrt_aux(int c, unsigned long long n){
    if (c == 0){
        return 1;
    } else {
        int k = (c - 1) / 2;
        unsigned long long a = isqrt_aux(c / 2, n >> (2*k + 2));
        return (a << k) + (n >> (k+2)) / a;
    }
}

unsigned long isqrt(unsigned long long n){
    if (n == 0){
        return 0;
    } else {
        unsigned long long a = isqrt_aux(( 63 - __builtin_clzll(n)) / 2, n);
        return n < a * a ? a - 1 : a;
    }
}

// ===========================================
// std::sqrt版 (nyaan_isqrt)　https://nyaannyaan.github.io/library/math/isqrt.hpp.html
// ===========================================
long long nyaan_isqrt(long long n) {
    if (n <= 0) return 0;
    long long x = sqrt(n);
    while ((x + 1) * (x + 1) <= n) x++;
    while (x * x > n) x--;
    return x;
}

// ===========================================
// 時間計測用
// ===========================================
inline double get_time_sec(void){
    return static_cast<double>(duration_cast<nanoseconds>(steady_clock::now().time_since_epoch()).count())/1000000000;
}

// ===========================================
// テスト実行関数
// ===========================================
void run_test(const string& range_name, const vector<unsigned long long>& inputs) {
    int TRIALS = 5;
    size_t N = inputs.size();
    
    cout << "--------------------------------------------------" << endl;
    cout << "Testing Range: " << range_name << endl;
    cout << "Data Size: " << N << " random elements" << endl;
    cout << "--------------------------------------------------" << endl;

    // --- Test 1: isqrt ---
    cout << "[ isqrt (Recursive Bitwise) ]" << endl;
    double total_time_isqrt = 0;
    for(int t = 0; t < TRIALS; t++){
        unsigned long long sum = 0;
        double start = get_time_sec();
        
        // 事前に生成した乱数配列に対して実行
        for(size_t i = 0; i < N; i++){
            sum += isqrt(inputs[i]);
        }
        
        double end = get_time_sec();
        double time_ms = 1000 * (end - start);
        total_time_isqrt += time_ms;
        cout << "  Run " << t + 1 << ": CheckSum = " << sum << ", Time = " << fixed << setprecision(3) << time_ms << " ms" << endl;
    }
    cout << "  >> Average: " << total_time_isqrt / TRIALS << " ms" << endl << endl;

    // --- Test 2: nyaan_isqrt ---
    cout << "[ nyaan_isqrt (std::sqrt based) ]" << endl;
    double total_time_nyaan = 0;
    for(int t = 0; t < TRIALS; t++){
        unsigned long long sum = 0;
        double start = get_time_sec();
        
        for(size_t i = 0; i < N; i++){
            sum += nyaan_isqrt(inputs[i]);
        }
        
        double end = get_time_sec();
        double time_ms = 1000 * (end - start);
        total_time_nyaan += time_ms;
        cout << "  Run " << t + 1 << ": CheckSum = " << sum << ", Time = " << fixed << setprecision(3) << time_ms << " ms" << endl;
    }
    cout << "  >> Average: " << total_time_nyaan / TRIALS << " ms" << endl << endl;
}

int main(){
    const size_t NUM_ELEMENTS = 100000000; // 10^8
    vector<unsigned long long> inputs(NUM_ELEMENTS);
    
    // 高速な乱数生成器 (メルセンヌ・ツイスタ 64bit)
    mt19937_64 rng(1333); 
/*
    // ------------------------------------------
    // パターン 1: [1, 10^9) の乱数
    // ------------------------------------------
    {
        cout << "Generating random numbers for pattern 1..." << endl;
        uniform_int_distribution<unsigned long long> dist(1, 1000000000ULL - 1);
        for(size_t i = 0; i < NUM_ELEMENTS; i++) inputs[i] = dist(rng);
        
        run_test("[ 1, 10^9 )", inputs);
    }
*/
    // ------------------------------------------
    // パターン 2: [10^12, 2*10^12) の乱数
    // ------------------------------------------
    {
        cout << "Generating random numbers for pattern 2..." << endl;
        // 10^12 から 2*10^12 までの範囲 (大きな桁のテスト)
        uniform_int_distribution<unsigned long long> dist(1000000000000ULL, 2000000000000ULL - 1);
        for(size_t i = 0; i < NUM_ELEMENTS; i++) inputs[i] = dist(rng);
        
        run_test("[ 10^12, 2*10^12 )", inputs);
    }

    return 0;
}

実行結果

考察

ランダムケースを見るに、「ニュートン法の方が$3.5$~$3.7$倍ほど高速である」と言えます。
また、連続ケースの $[10^{12},10^{12}+10^8)$ の場合、とても速くなっています。自分では分からなかったのでGeminiに聞いたところ、コンパイラが再帰の結果をキャッシュしてるから速いと言われました。ランダムケースでは最適化が掛からなかったので、おそらく正しいと思われます。

ニュートン法は「最速」であるか？

ここまでダラダラと書いて来ましたが、別にニュートン法は、二分探索より速いだけで、最速ではありません。ご存知かもしれませんが、以下のようにする方が圧倒的に速いです。

Nyaan's Library： https://nyaannyaan.github.io/library/math/isqrt.hpp.html

要するに、「組み込み関数のsqrtを切り捨てて、誤差を調整する」という手法を取っています。これを含めた実行時間の表はこのようになります。

全然勝ててませんね...ランダムケースだと $5\sim 7$ 倍の差を付けられています。 唯一、連続 $[10^{12},10^{12}+10^8)$ のケースで勝っています。これは再帰関数でキャッシュが残る夕いつの利点を活かした勝利でしょう。
ただし、実用的には連続区間なら商列挙のようなことをすれば $O(\sqrt{N})$ で計算できるので、正直あんまり意味はないですね...

結論

CPU命令速い!!!!!!
でもニュートン法も頑張ってるので許してください。俺はニュートン法を使います()

参考

isqrtの内部実装：
二分探索isqrtの実装：二分探索isqrtとして測定に使わせていただきました(intをllに変更などしましたが)。ビット演算を巧妙に使ってて自分には理解出来ていません(すごい) ← おい
Nyaan's Library の isqrt：やっぱCPU命令にはかなわんのや...
(Youtube) One second to compute as many square roots as I can：海外ニキの動画、このブログの上位互換です

終わりに

ここまで見ていただきありがとうございました(自分のメモを兼ねて書いたブログなので、雑な部分を多いと思います)。「わざわざ証明なんか見なくても動けばいいだろ！」と思うかもしれませんが、個人的には証明を終えて楽しかったです。

明日の投稿者は@Suimaと@nzt3さんです。