高速ゼータ変換のお勉強

この記事は, 2024 夏のブログリレー 1 日目の記事です. はじめに https://atcoder.jp/contests/arc136/tasks/arc136_d を解いたときに新しく勉強したことがあったので, 忘れないように書いておきます. ※本記事の後半にはこの問題の解法を述べる部分があります. ゼータ・メビウス変換について まず, ゼータ・メビウス変換の基本的な知識をまとめます. ゼータ変換 数列の添字をまとめた添字集合 J を考えます. このときに, この集合で半順序関係 ⪯ が成立して, かつ関数 f(x) が任意の x∈J で定義されている時, f をゼータ変換した関数 F を次のように定義します. F(n)=x⪯n∑ f(x) 半順序関係 ある集合 S について,

東京科学大学デジタル創作同好会traPOxojo

去年も同じようなタイトルのブログを投稿してますね。

はじめに

この記事は、緋月ゆいさんの朝雑を聴きながら書いています。

とてもかわいい VTuber さんですね。私は大好きです。

本題

Codeforces Round 895 - E の解説の冒頭です。

However, of course, we do not expect participants in Div3 to have knowledge of these advanced data structures, so there is a simpler solution.

Div.3 に出る方々はセグ木や平方分割は知らんだろう、と書いてありますね。せっかくなので知っておきましょう。ちなみにいろいろ書いていたら長くなってしまったので、この問題に関する記述はないです。

セグ木はすでに記事がありますね～

セグメント木・遅延セグメント木を考える

はじめに この記事は2024夏のブログリレー24日目の記事です。(投稿が1日遅れてしまいました、すみません...) こんにちは、24Bの@zoi_dayoです。セグメント木、発想はまあまあシンプルなのに計算量がうまく小さくなっていておもしろいのでまとめてみます。使ったことがない人、使ったことはあるけど構造よくわかってない人におすすめです。 想定読者は緑〜くらいのイメージです。 セグメント木とは (Segment Tree) たとえば、長さNの数列の区間[l,r)の最大値を取得することを考えます。また、クエリの途中で一部の値を変更したいです。現在の状態を配列に保存して真面目に計算すればクエリあたりO(N)なのですが、高速化したいですね。ここで、[0,2),[2,4),...の結果、[0,4),[4,8),...の結果、...などを前計算しておきます。話を簡単にするために要素数Nを2のべき乗として、各区間の担当範囲を図示すると、こんなふうになります。(現実には長さは2のべき乗ではないのですが、後ろの余った部分を後述するeで埋めればうまく動きます) 前計算の個数は、1+2+4

東京科学大学デジタル創作同好会traPzoi_dayo

お気持ち

Range Sum Query を考えます。

Segment Tree で一発です。ただ、今回は少し別のアプローチを考えてみましょう。

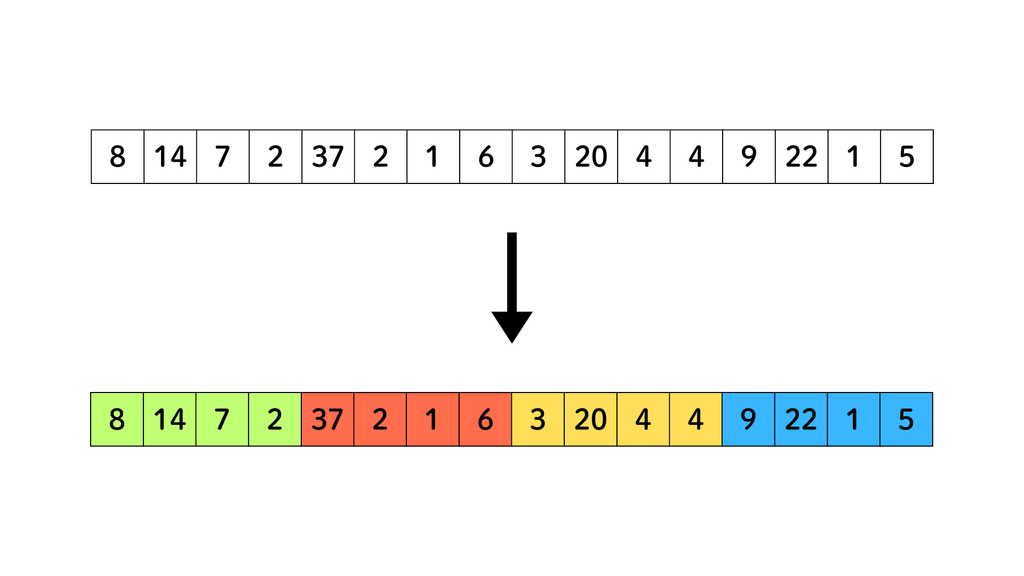
Segment Tree では、隣同士の 2 個の要素を合わせたブロックみたいなものを考えて、二分木チックな構造を作っていました。今回は、木のようなものは作らずに、$\sqrt{n}$ 個の要素で $1$ つのブロックを構成するようにまとめてみましょう。

例えば、長さ $16$ の数列を考えると、上図のように $4$ つごとのブロックに分けることができますね。このようなブロックのことを「バケット」と呼びます、

次に、それぞれのバケットに対して総和を計算してあげます。

準備はこれでおしまいです。それでは各クエリを処理していきましょう。

• 1 : 配列の $i$ 番目を更新して、それが含まれるバケットの総和を更新します。
• 2 : 区間 $[l,r)$ の中に完全に含まれるバケットと、そうでないバケットに分けます。完全に含まれるバケットそれぞれの総和と、それに含まれていない各要素をすべて足し合わせたものを出力します。

クエリ 2 の処理が少しわかりにくいかもしれませんが、例えば $[3,12)$ の場合は次の図のようになります。

肝心なのは計算量ですね。クエリ 1 は自明に $O(1)$ っぽいですね。では、クエリ 2 はどうでしょうか。

まず、先ほどの分け方から、存在するバケットの個数は $O(\sqrt{n})$ 個です。そのため、バケットの総和として足される数は高々 $\sqrt{n}$ 個くらいというわけですね。

また、各要素を足し合わせる部分ですが、例えば先ほどの図で、黄色のバケットに含まれる各要素をすべて見るといったことは起こり得ません。もしそのような状況があれば、各要素を見るのではなく、そのバケットの総和を足すことになるからです。というわけで、黄色のバケットのうち見られる要素は $\sqrt{n}$ 個未満ということになります。左の緑色のバケットに対しても同じことが言え、結果として各要素を足し合わせる部分では、$2\sqrt{n}$ 個以上の要素を見ることは起きません。

というわけで、単純に計算すると、クエリ 2 の計算量は $O(\sqrt{n})$ ということが分かりました。以上より、このようにすると Range Sum Query が処理できました。

このように、$n$ 個の要素を $\sqrt{n}$ 個の塊に分割してあげる、といったテクニックを平方分割といいます。

平方分割における遅延伝搬

Segment Tree に Lazy Segment Tree があったように、平方分割にも遅延伝搬を行う平方分割は存在します。とはいえ、大きなところは遅延セグ木とそんなに変わらないと思います。

今回の Update は可換でないので、遅延伝搬をしてあげましょう。

今回は、バケットごとに Lazy という値を持たせます。例えば、図のように $a_3,\dots ,a_9$ を $5$ に変更させてみましょう。

丸で囲った部分が、値が変化した場所です。先ほどと同じように、バケットを完全に含む場所については Lazy に変化を保存させて、そうでないところは直接保存させてあげます。

これは $O(\sqrt{n})$ でできそうですね。

では、この状態から、$a_6$ を求めてみましょう。$a_6$ が含まれているバケットは Lazy に $5$ の値を持っているので、この時点でバゲット内のすべての要素に対して反映してあげます。

この伝搬は、バケット内の要素の個数が $O(\sqrt{n})$ なことから $O(\sqrt{n})$ でできます。これを終えたら、$a_6$ をそのまま出力すればよいです。

この問題でありうるもう一つのシチュエーションとしては、次の図のような状態で $a_3,\dots ,a_{10}$ を $7$ に変更するようなものがあります。

$a_3,a_4$ はそのまま $7$ に変更すればよく、$a_5,a_6,a_7,a_8$ は完全にバケットを含むので Lazy の値を $7$ に変更すればよいです。問題は、まだ伝搬を行っていないバケットを完全に含まないような区間になっている ($a_9,a_{10}$ さん...) 場合ですね。

先述のように、Update は可換ではないので、先に黄色のブロックの 3 を伝搬させてしまってから、$a_9,a_{10}$ を変更してあげればよいですね。伝搬は $O(\sqrt{n})$ なので、このシチュエーションでも Update クエリは $O(\sqrt{n})$ で行うことができます。

それ、セグ木でよくない？

Range ○○ Query みたいなのは世の中にいろいろあるわけですが、結局十分大きい $n$ について $\log n<\sqrt{n}$ なので、計算クエリはセグ木・遅延セグ木のほうが速いから、計算量的にはセグ木でやったほうがよくない？と感じる方もいるでしょう。実は、計算量だけではわからない平方分割のありがたみがあります。

その 1 : 平方分割は、バケット上に重いデータ構造を乗せることが可能です。セグ木でやるとすべてのノード上に構造を乗せることになってしまって爆発しちゃいますが、平方分割だと空間計算量が $O(n)$ で済んだりとか、そういう感じの恩恵を得ることができます。

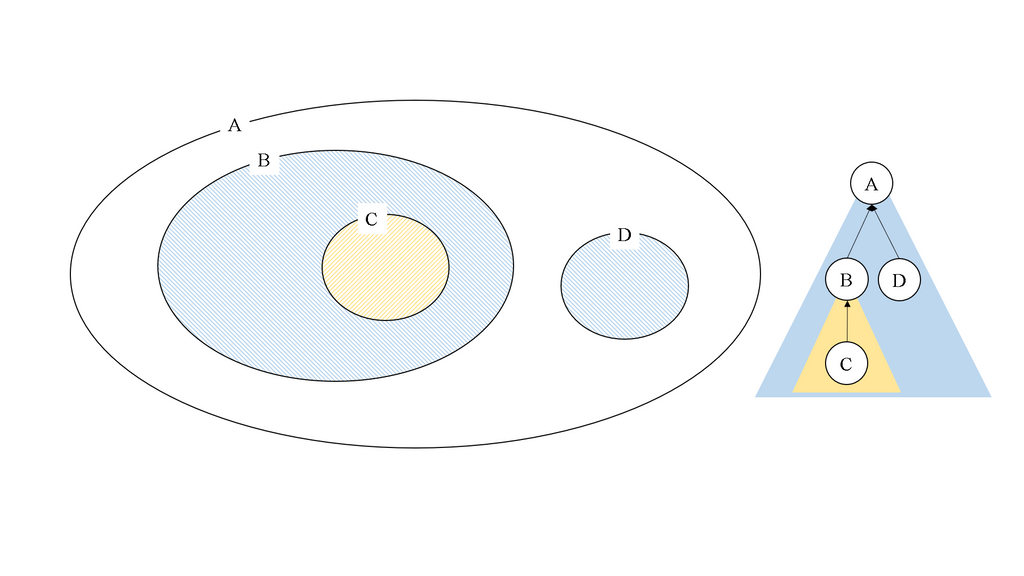
その 2 : Segment Tree を使うためには必要な制約があって、この構造に持たせる要素はモノイドの元でなければなりません。

すると、Segment Tree に載るようなうまいモノイドが設計できないときに、くるし～ってなります。苦しいときには平方分割がたすけてくれるかもしれません。

モ～

問題の条件によっては、そのような場合に Mo's Algorithm が適用できる場合があります。名前の由来は牛さんの鳴き声です。嘘です。

Mo's Algorithm が適用できる条件は次の 3 つです :

1. 要素が更新されない
2. クエリの先読みが可能
3. 区間 $[l,r]$ の結果から、区間 $[l,r+1],[l,r-1],[l+1,r],[l-1,r]$ の結果を容易に計算できる。

試しに 1 問解いてみましょう。

モノイドが思いつきません。くるしいですね。Mo で解けないかやってみましょう。

問題の形式から、「1. 要素が更新されない」「2. クエリの先読みが可能」はわかりますね。では、3 がどうなるかを見てみましょう。

区間 $[l,r]$ における整数 $i$ の個数を $A_{[l,r]}(i)$ とします。求める答えは ${\sum }_{i=1}^n\lfloor A_{[l,r]}(i)/2\rfloor$ です。

ここから、区間 $[l,r+1]$ に広げることを考えてみます。このとき、区間に $a_{r+1}$ が追加されます。すると、$[l,r]$ の時に $A_{[l,r]}(a_{r+1})$ が奇数であれば答えは $+1$ され、偶数であれば答えは変わりません。$[l,r-1],[l+1,r],[l-1,r]$ についても同様に考えることができ、区間の長さを 1 変えたときの遷移は $O(1)$ で行えそうだということが分かります。これで、3. の条件も満たすことが分かりました。

ここまでチェックできれば、Mo's Algorithm の出番です。平方分割っぽさがないなと思いながら読んでいたみなさま、お待たせいたしました。

まず、区間 $[1,n]$ を $\sqrt{Q}$ 個の区間に分割します。そして、それに基づいて $Q$ 個のクエリをソートします。ソートの仕方としては、左端のブロックの位置 -> 右端の位置 の順でソートする感じです。

言葉だと表現が難しいですが、ソートのイメージはこんな感じです。
そして、尺取りみたいな感じで処理してあげます。やることはこれだけです。

時間計算量を見積もってみます。左端と右端がそれぞれ何回動くかを考えればよいです。

• 左端 : ブロックごとにまとめているので、1 回のクエリにつき $O(n/\sqrt{Q})$ 回動く。クエリは $Q$ 回あるので $O(n\sqrt{Q})$ 回動く。
• 右端 : ブロックごとに、$O(n)$ 回動く。ブロックは $O(\sqrt{Q})$ 個あるので、$O(n\sqrt{Q})$ 回動く。

つまり、1 回の遷移にかかる時間が $O(\alpha )$ であるとき、$O(\alpha n\sqrt{Q})$ でクエリをすべて処理できます。今回の場合、遷移には $O(1)$ かかるので、$O(n\sqrt{Q})$ で解けました。