はじめに
この記事は2024夏のブログリレー24日目の記事です。(投稿が1日遅れてしまいました、すみません...)
こんにちは、24Bの@zoi_dayoです。
セグメント木、発想はまあまあシンプルなのに計算量がうまく小さくなっていておもしろいのでまとめてみます。使ったことがない人、使ったことはあるけど構造よくわかってない人におすすめです。
想定読者は緑〜くらいのイメージです。
セグメント木とは (Segment Tree)
たとえば、長さNの数列の区間[l,r)の最大値を取得することを考えます。また、クエリの途中で一部の値を変更したいです。現在の状態を配列に保存して真面目に計算すればクエリあたりO(N)なのですが、高速化したいですね。ここで、[0,2),[2,4),...の結果、[0,4),[4,8),...の結果、...などを前計算しておきます。話を簡単にするために要素数Nを2のべき乗として、各区間の担当範囲を図示すると、こんなふうになります。(現実には長さは2のべき乗ではないのですが、後ろの余った部分を後述するeで埋めればうまく動きます)
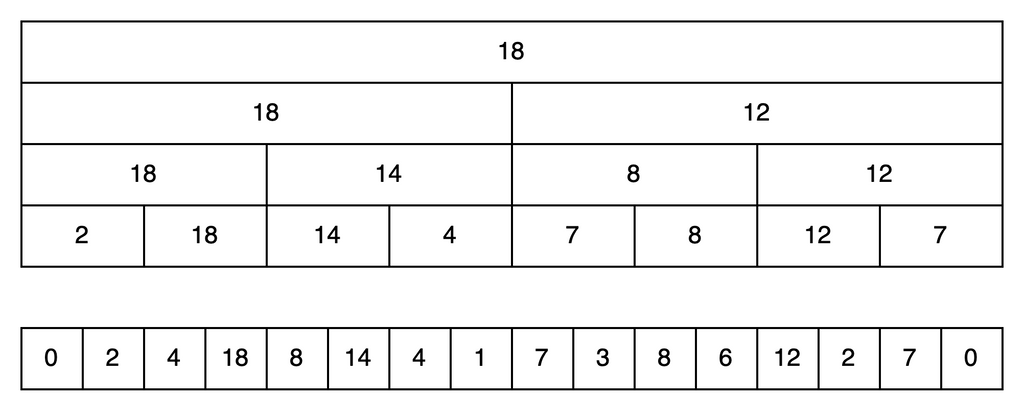
前計算の個数は、1+2+4+...+(N/2)で、合計N-1個です。下側から計算することで、それぞれの範囲の値は、2つの要素のmaxで求められるので、前計算はO(N)となります。
たとえば[3,11)の最大値を求めたいときは、下図のように4つの領域の最大値を取るだけでよいです。
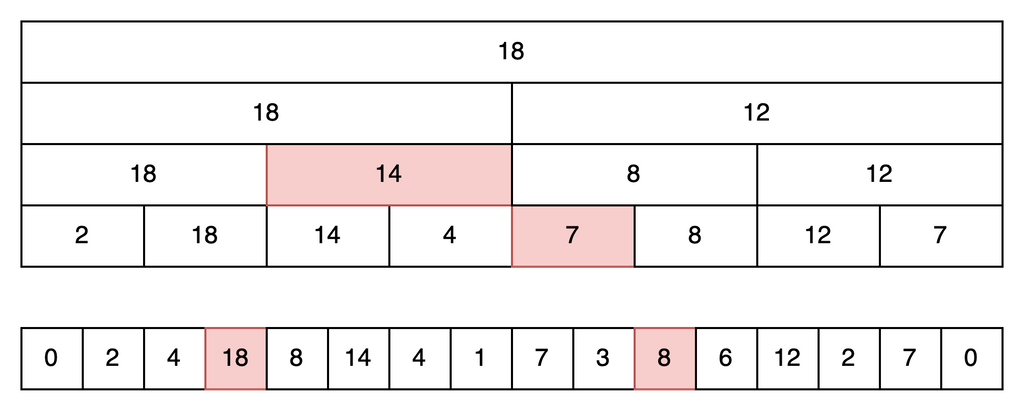
色々試してみると、これで選ばれる要素は山のように配置されていることがわかります。そして、連続して横に2つ並ぶことは(山の頂上を除いて)ありません。よって、山の上り下りでそれぞれ最大N個の要素を見れば答えが出るわけですね。
これがセグメント木の発想です。木...?と思うかもしれませんが、各区間をノード、その更新のために必要な2つの区間を子として見れば、これは二分木ですね。区間(セグメント)をノードにした木なのでセグメント木です。
今回の場合、区間のmaxを求めることを考えましたが、これが総和や掛け算だとしてもいい感じに動きます。他の関数でも良いです。ただし、f(f(a, b), c) = f(a, f(b, c))が成立するT f(T a, T b)と、f(e, a) = f(a, e) = eが成立するT e(単位元)を定義しないといけません。ちなみに、このようなT, f, eの組を「モノイド」と呼ぶらしいです。たとえばmaxを求めるためには、T = int、f = [](int a, int b){return max(a,b);}、e = -INF (問題による)みたいにすればよさそうです。これさえできれば、長さNの配列に対して、前計算O(N)で、どんな区間に対しても答えをO(logN)で求めることができる魔法のデータ構造です。
では、配列の値を更新した場合を考えます。この場合、O(N)かけて前計算をやり直す必要はなく、その点を含む区間だけを更新すればよいです。木を上にたどる感じになり、これはO(logN)ですね。
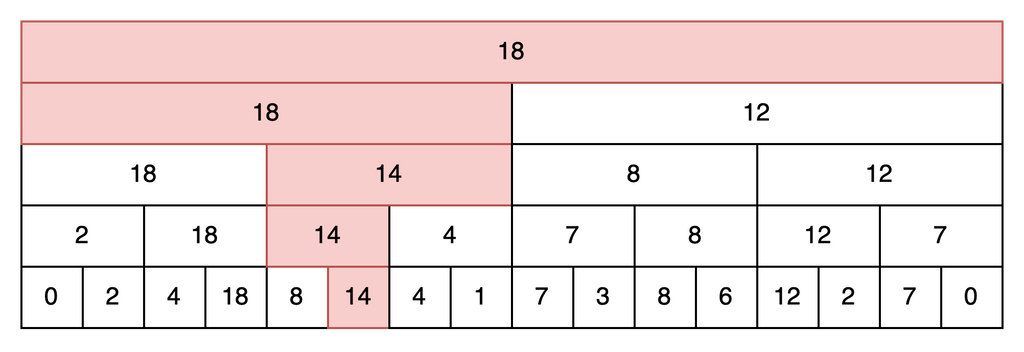
まとめると、セグメント木を使うと、前計算O(N)、区間演算O(logN)、一点更新O(logN)になります。
実装例は以下。
#include <bits/stdc++.h>
using namespace std;
template <typename T>
struct SegmentTree {
int n;
vector<T> data;
T e;
function<T(T, T)> f;
SegmentTree(int n, T e, function<T(T, T)> f) : n(bit_ceil((unsigned)n)), e(e), f(f) {
data.assign(2 * this->n, e);
}
T query(int l, int r) { return _inner_query(l, r, 1, 0, n); }
void update(int i, T x) {
i += n;
data[i] = x;
while (i > 0) {
i >>= 1;
data[i] = f(data[i << 1 | 0], data[i << 1 | 1]);
}
}
private:
T _inner_query(int l, int r, int i, int il, int ir) {
if (r <= il || ir <= l) return e;
if (l <= il && ir <= r) return data[i];
int m = (il + ir) / 2;
return f(__inner_query(l, r, i << 1 | 0, il, m),
__inner_query(l, r, i << 1 | 1, m, ir));
}
};
// https://judge.yosupo.jp/problem/staticrmq
int main() {
int n, q;
cin >> n >> q;
SegmentTree<int> seg(n, numeric_limits<int>::max(), [](int a, int b) { return min(a, b); });
for (int i = 0; i < n; i++) {
int a;
cin >> a;
seg.update(i, a);
}
for (int i = 0; i < q; i++) {
int l, r;
cin >> l >> r;
cout << seg.query(l, r) << endl;
}
}
区間更新がしたい! (Lazy Segment Tree)
区間加算や区間変更など、区間をまとめて更新できればうれしいですね。よく考えてみると、区間クエリが飛んできた時、すべてのノードを使うわけではないです。ということは、更新クエリが来たときに真面目に全部更新しても、結局使われないまま次の更新が来るノードがありそうです。この方針で考えてみましょう。つまり、更新クエリが気たとしても、必要になるまで下層に伝えないようにします(=遅延させます)。
この場合、区間更新に関しては、区間取得のときと同じようにノードを選び、それらに対して適用をすればよいです。ただし、この際に、更新したいノードの祖先が遅延しているは下に伝えておく必要があります。こうなると更新するノード数がO(logN)に収まらないような気持ちになってしまうのですが、よく考えると、この「遅延を解消しなければならないノード」は、各階層だけで見ると右端または左端(またはその両方)です。つまり、遡らなければならない個数は\O(\log N)となるので、合計でO(logN)個のノードの情報を更新するだけでよいことになります。

では結果取得のときはどうでしょう。この際も、必要なノードの上側の遅延を解消して、その後に普通にセグ木をすればよいです。先ほどと同じく前半はO(logN)でできるので、合計でもO(logN)でできます。計算量としてはセグ木と変わりませんね。(もちろん定数倍は悪化していますが)
これを遅延セグメント木といいます。
これができる条件を確認してみます。もちろん普通のセグ木の条件、つまり演算対象はモノイドでないといけない、という条件は引き継がれていますが、今回はそれに加えて「値変更のための演算」があります。操作に対してもセグ木っぽいことをしていることからわかるように、操作もモノイドでないといけません。まとめると、値のモノイドの条件としてT f(T a, T b)、T e、操作のモノイドの条件としてF g(F a, F b)、F id、また操作の内容としてT h(F fn, T x)が必要です。例えば区間総和を求めるセグ木を加算変更クエリに対応させるのであれば、T = struct {int sum, length}、f = [](T a, T b){return {a.sum + b.sum, a.length + b.length};}、e = {0, 0}、F = int、g = [](int a, int b){return a+b;}、h = [](int fn, T x){return {x.sum + x.length * x, x.length};} みたいになります。いっぱいあって大変ですね。
ここで、区間総和のセグ木だと思ってT = intとしてはいけません。hは、「ある区間についての答えはxです。では、この区間全体に対して操作fnをしたなら、区間の答えは何になりますか?」という関数なのですが、区間総和・区間加算の場合は区間の長さによって答えがどれだけ変わるかが変化してしまいます。そのため、区間の長さをデータとして持っておかなければうまく遅延セグメント木に乗せることができません。もちろん、区間総和でなく区間minなどであった場合、変化後の値が区間の長さによらないので、普通にT = intとしてOKです。個人的にはここが一番ムズポイントだと思ってます。h(int fn, int x, int length)のように、h自体から区間の長さを得られるようにしたほうがいいかもしれません。
実装例は以下。
#include <bits/stdc++.h>
using namespace std;
template <typename T, typename F>
struct LazySegmentTree {
int n;
T e;
F id;
vector<T> tree;
vector<F> lazy;
function<T(T, T)> merge;
function<T(T, F)> apply;
function<F(F, F)> compose;
LazySegmentTree(int n, T e, F id, function<T(T, T)> merge, function<T(T, F)> apply, function<F(F, F)> compose) : n(bit_ceil((unsigned)n)), e(e), id(id), merge(merge), apply(apply), compose(compose) {
tree.assign(2 * this->n, e);
lazy.assign(2 * this->n, id);
}
LazySegmentTree(vector<T> a, T e, F id, function<T(T, T)> merge, function<T(T, F)> apply, function<F(F, F)> compose) : n(bit_ceil(a.size())), e(e), id(id), merge(merge), apply(apply), compose(compose) {
tree.assign(2 * n, e);
lazy.assign(2 * n, id);
for (int i = 0; i < a.size(); i++) tree[n + i] = a[i];
for (int i = n - 1; i > 0; i--) tree[i] = merge(tree[i << 1 | 0], tree[i << 1 | 1]);
}
void apply_lazy(int i) {
if (i == 0) return;
if (lazy[i] == id) return;
if (i < n) {
lazy[i << 1 | 0] = compose(lazy[i << 1 | 0], lazy[i]);
lazy[i << 1 | 1] = compose(lazy[i << 1 | 1], lazy[i]);
}
tree[i] = apply(tree[i], lazy[i]);
lazy[i] = id;
}
void update(int l, int r, F f) {
_inner_update(1, 0, n, l, r, f);
}
T query(int l, int r) {
return _inner_query(1, 0, n, l, r);
}
private:
void _inner_update(int i, int l, int r, int ql, int qr, F f) {
apply_lazy(i);
if (l > qr || r < ql) return;
if (ql <= l && r <= qr) {
lazy[i] = f;
apply_lazy(i);
return;
}
if (i < n) {
int m = (l + r) >> 1;
_inner_update(i << 1, l, m, ql, qr, f);
_inner_update(i << 1 | 1, m, r, ql, qr, f);
tree[i] = merge(tree[i << 1], tree[i << 1 | 1]);
}
}
T _inner_query(int i, int l, int r, int ql, int qr) {
apply_lazy(i);
if (l >= qr || r <= ql) return e;
if (l >= ql && r <= qr) return tree[i];
int m = (l + r) >> 1;
return merge(_inner_query(i << 1, l, m, ql, qr), _inner_query(i << 1 | 1, m, r, ql, qr));
}
};
// https://judge.yosupo.jp/problem/range_affine_range_sum
using ll = int64_t;
int main () {
ios::sync_with_stdio(0);
cin.tie(0);
const int MOD = 998244353;
int n, q;
cin >> n >> q;
vector<ll> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
struct T {
ll x;
int len;
};
struct F {
ll a, b;
bool operator==(const F &f) const = default;
};
vector<T> v(n);
for (int i = 0; i < n; i++) v[i] = {a[i], 1};
LazySegmentTree<T, F> seg(v, {0, 0}, {1, 0}, [](T a, T b){return T{(a.x + b.x) % MOD, a.len + b.len};}, [](T a, F f){return T{(f.a * a.x + f.b * a.len) % MOD, a.len};}, [](F a, F b){return F{a.a * b.a % MOD, (a.b* b.a + b.b) % MOD};});
for (int Q = 0; Q < q; Q++) {
int type;
cin >> type;
if (type == 0) {
int l, r, b, c;
cin >> l >> r >> b >> c;
seg.update(l, r, {b, c});
} else {
int l, r;
cin >> l >> r;
cout << seg.query(l, r).x << '\n';
}
}
}
この他にも、2次元平面上の長方形クエリに対してO(logHlogW)で答えられる「2次元セグメント木」、区間和の場合に使える定数倍の良い「Fenwick Tree」、O(logN)時間での任意位置挿入・削除や分裂・連結、区間反転ができる「平衡二分探索木」、これまでの状態をすべて保持していつでも移動できる「永続セグメント木」などいろいろあります。実際に問題に使えるかどうかはさておき、普通のセグ木の構造と比較して見てみると楽しいです。
さいごに
セグ木、普通のものならばそんなに実装も重くないのですが、乗せるものによっていろんな事ができて面白いです。ACLがあるので中身を理解していなくてもどうにかなるのですが、せっかくなので理解できると楽しいです。
