この記事は夏のブログリレー2日目の記事です。

25B の jibjib です。AtCoder のユーザー名は rhoo です。競技プログラミングをやっており、ARC や AHC によく参加しています。
ちょうど夏休みが始まった 8 月 1 日から 8 月 11 日 にかけて、THIRD プログラミングコンテスト 2025 夏（AtCoder Heuristic Contest 051）が開催されていました。240 時間の長丁場で過酷^[1]なコンテストですが、健闘して最終的に 6 位になれたので、せっかくですし参加記を書いてみました。日記みたいになっていますが、コンテスト中に書いていたわけではなく、提出履歴などから当時の思考過程を思い出して書いています。

Day1

問題文を読む。

問題文を雑に要約すると ：

• ごみ搬入口に運ばれたごみをできるだけ正しい処理装置に分別できるように、分別器、処理装置、それらをつなげるベルトコンベアを 2 次元平面上に設置する。
• ごみは 5～20 種類。処理装置はごみの種類数と同数。分別器は 5～80 種類あり、合計で 50～1000 個設置可能。
• 処理装置と分別器は設置可能な座標が 2 次元平面上で固定されており、入力で与えられる。ごみ搬入口の座標は (0, 5000) で固定。
• 分別器は入力（0 個以上のベルトコンベア）と出力（2 つのベルトコンベア ： 出力 0 / 出力 1）を持つ。入力から来たごみを、分別器の種類とごみの種類から決まる確率で出力 0 に流し、そうでなければ出力 1 に流す。種類 $i$ の分別器が種類 $j$ のごみを出力 0 に流す確率は 0.1～0.9 のランダムな実数で決まる。出力 0 と出力 1 は行き先が同じでも構わない。
• ベルトコンベア同士は交差してはならない。また、搬入口・分別器・処理装置を頂点としてベルトコンベアを辺とする有向グラフは閉路なし（DAG）でなければならない。
• スコアは、ごみが間違った処理装置に送られる確率。これをできるだけ小さくするのが目標となる。
• 順位表は相対評価。各テストケースごとに「全参加者中の最小スコア / 自身のスコア」が相対評価スコアとして与えられ、その和が提出の得点となる。

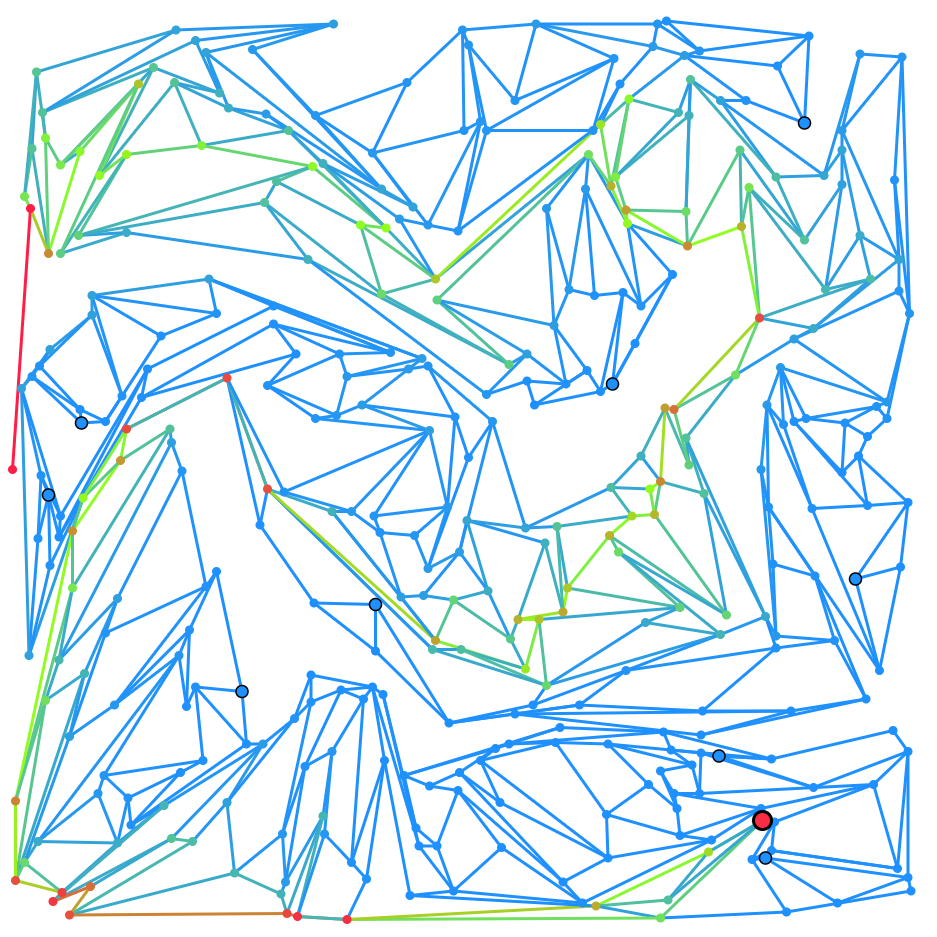
サンプルのビジュアライズ結果はこんな感じ。

ビジュアライズした図に登場する丸は分別器か処理装置の設置可能な座標を表していて、小さい丸が分別器、大きい丸が処理装置を表している。また色は、ある特定の種類のごみが各辺や各頂点を通る確率を表していて、確率が高いほど赤く、低いほど青くなっている。
このケースでは 13 種類のごみがあり、処理装置は 2 つしかつなげていないので、11/13 ≒ 84.6% 以上のスコアになる。また、つなげている処理装置は設置した分別器が最も正確に分別できるごみに対応した処理装置になっているため、2/13 のごみは 90% くらいの精度で正しい処理装置に到達できていそうで、スコアは 11/13 + 2/13 × 0.1 ≒ 86.2% くらいになるはず。実際は 86.5% で、この理解は正しそう。

幾何が必要で、実装が大変になりそうな予感。

Day2

入出力とユーティリティを整備して、すべてを処理装置 0 に突っ込むやつを書く。

いい感じのグラフを作ってから分別器の割り当てを決めるのが楽そう。どういうグラフがいいのかはよくわからないので、とりあえず頂点数が多めのグラフを作るため、てきとうな BFS を実装した。長い辺をできるだけ作らないために、一番短い辺でつなげられる頂点を追加していく。（ただし、途中で辺の交差が発生しないように注意しつつ。）

分別器の割り当ては焼きなまし^[2]でほぼ最適にできるはず。最終的な解法でも必要になりそうだし、実装もそこまで大変ではないので高速化してしまう。前からの DP（$fd{p}_{v,i}:=$ 頂点 $v$ に種類 $i$ のごみが来る確率）と後ろからの DP（$bd{p}_{v,i}:=$ 頂点 $v$ に種類 $i$ のごみが来たときに正しい処理装置に行ける確率）を計算すると、変更のたびに DP を全頂点で再計算する必要がなくなり、$O(\text{ごみの種類数})$ での差分計算が可能になる。

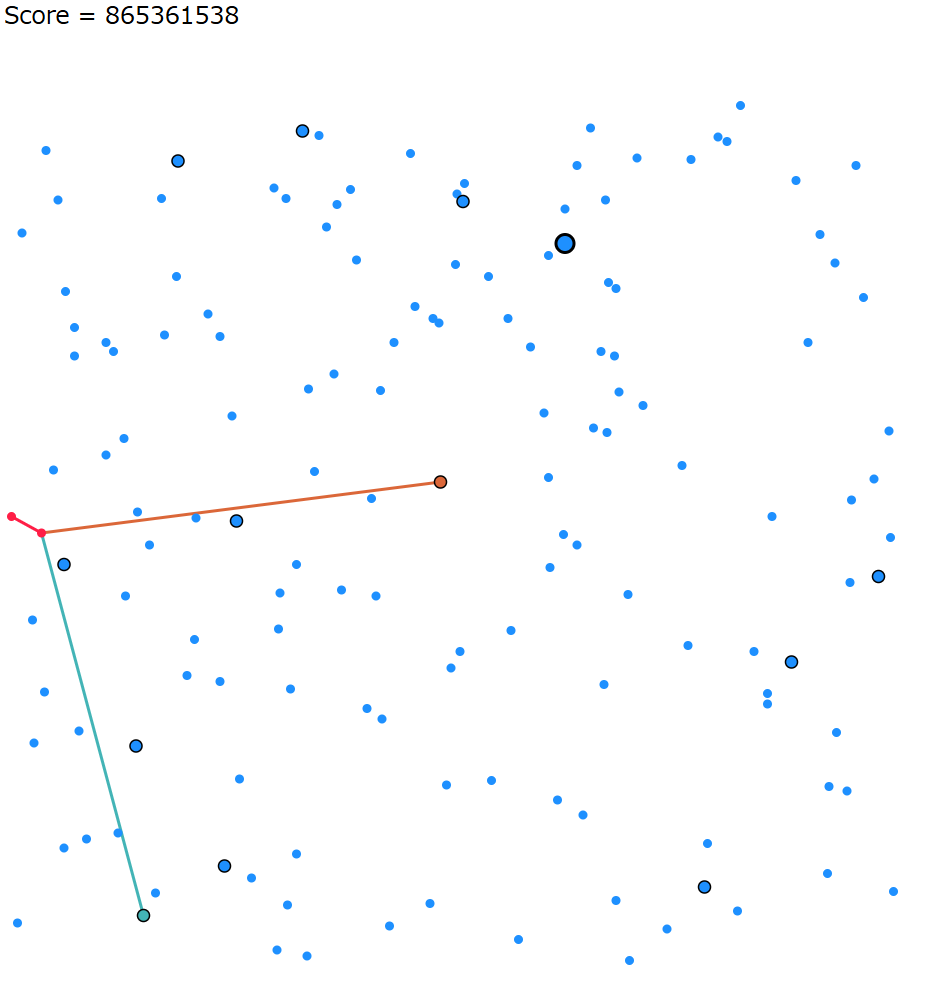
提出時 10 位。長期コンテストはみんな出だしが遅いので参考にはならない。最終順位の 200 位くらいに相当する。

頂点数の多いグラフにはなっているけど、一部の処理装置がつなげられていなかったり、壮大に分別器をつなげているもののそこから到達可能な処理装置が 1 種類しかないせいでまったく分別に寄与していなかったりなど、明らかに無駄がある。しかも、そもそも辺をつなげられていない分別器がたくさん残っている。最終的に処理装置に到達できない辺は削除しているためだが、ここらへんの分別器をうまく組み込めたらまだまだ強くなりそう。

グラフの形の簡単な考察：

• グリッド ： ごみが A, B の 2 種類のとき、分別器 (0, 0) から始めて A の確率が高そうだったら (x, y) → (x+1, y) に移動し、 B の確率が高そうだったら (x, y) → (x, y+1) に移動することを繰り返し、 A と B を分別する。
• 二分木 ： グリッドを組み合わせてごみを 2 分割していく。間違った判断がされうる回数が少ないのが売りだが、頂点数が少ないケースが苦手。
• パス ： グリッドを組み合わせてごみを一つずつ判別していく。グラフの構築が楽。二分木が苦手なケースでも安定してる。

少し試す限りでは、二分木とパスだとパスのほうがよさそう。かなり雑な実験だけど。パスの方がグラフの構築も楽だし、パスでいいかな。
あとはパスベースのいろんなグラフを作ってスコアの増減を観察してみると、

• 均等ではなく、ランダムに処理装置があったら、 30% くらいスコアが悪化した。
• グリッド幅は 4～6 くらいがよさそう。
• グリッド幅が同じであれば多少辺のつなぎ方を変えてもスコアに大きな変化はない。
• 分別器の数を本来の 75% にしてもスコアの悪化は 10% くらい。

などがわかる。まずは、処理装置の位置を考慮したルート取りが重要になってくるのかな。

Day3

グリッドの埋め込み、どうしよう。完璧にグリッドを埋め込めなくても、頂点素なパスがいい感じに隣接していればいいのだけど。ChatGPT にビジュアライザを書かせ、手で解けるようにしたら、できなくはない感じ。

ぐるぐる

背景のグリッドを意識して解く

処理装置がまんべんなく登場してほしいし、自由度が高い後者のほうがいいのか？ ただ、頂点密度によって成功したりしなかったりしそうで調整が面倒そう。というか、ここから異なるパスの間に辺を追加したグラフを焼きなましに渡してもあまりスコアが出ない。追加できてる辺の数が少ないことが原因みたい。
いったん提出してみたいし、分別器集合をグリッド状に分割して埋め込むようにする。縦と横の直線で 2 次元平面を分割して、各マスからそのマスの領域に含まれている分別器を一つずつ選んでグリッドを作る。まず横方向の直線を分別器の数が均等になるように 4 本入れて、次に縦方向の直線を一つも分別器が入っていないマスができないように貪欲に入れる。さらに、使われなかった分別器を近場に埋め込んだりして最終的なグラフを作った。

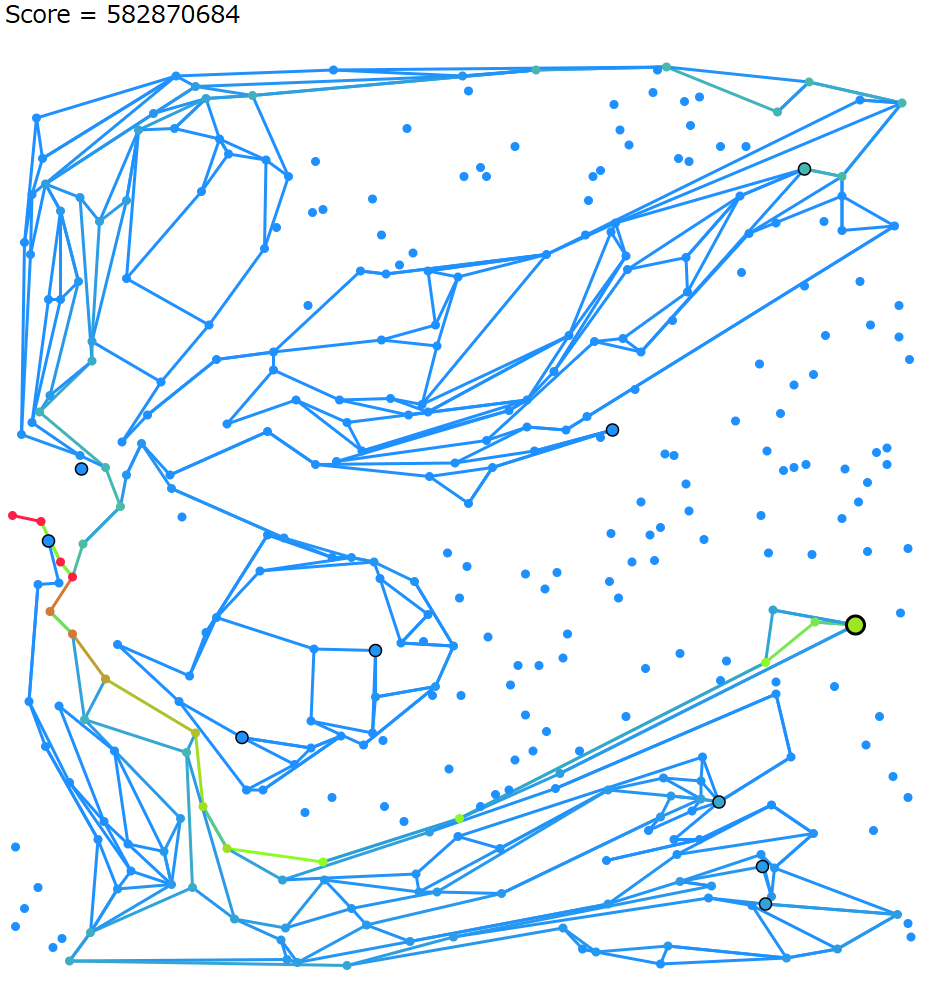
提出時 10 位。最終 100 位くらい。

使われなかった分別器を埋め込む方法が雑で、分岐のない分別器が大量発生しているのを除けば、思ったとおりに動いておりいい感じ。

Day4

グリッドの埋め込み、何もわからない。
$5\times H$ のグラフが埋め込めたら $5\times (H+1)$ のグラフを作りに行くようにして、辺の交差は許容せず、一部の頂点は割り当てなしを許容して、できるだけ多くの頂点が割り当てられるように山登り^[3]をしてみたけど、見るからにだめなグラフが生成される。

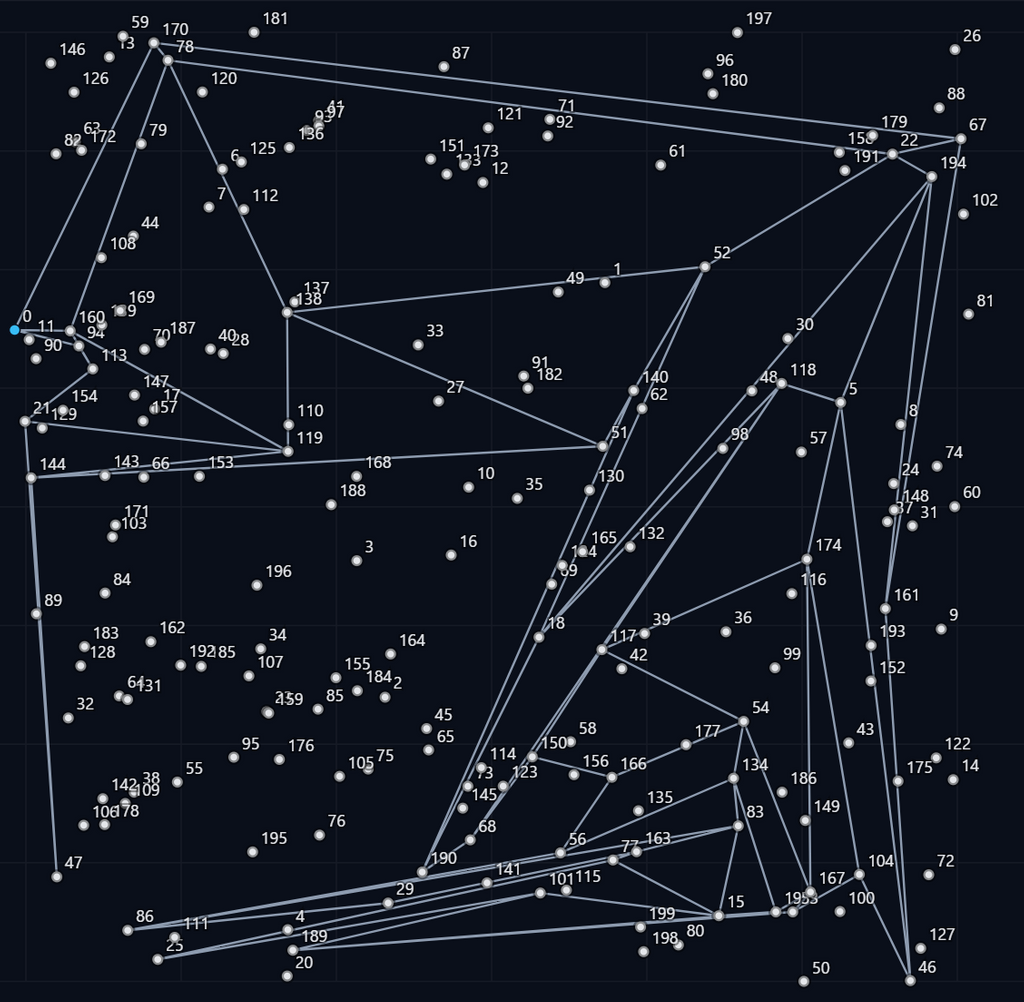
うーん、交差しないようにする以前に、短い辺を使ってほしい。距離の総和を最小化する焼きなましをしたらうまくいったりしないかな。

うまくいった。少し交差が残るけど、これくらいだったら微調整でどうとでもなりそう。

さらに、焼きなましで見つけた配置を山登りで交差を最小化するようにした。これによって、グリッド幅 5 のグラフであれば全分別器を使用する場合は埋め込みに成功する確率が 10%、90% の分別器を使う場合は 30% になった。

ただ、実行時間制限に間に合わせるために、山登りの高速化が必要。辺の交差判定に $O(\text{辺の数})$ かかっているが、登場する線分はだいたい短いので、 2 次元平面をセルで分割して、同じセルを共有する線分のみ交差判定の対象とする。
つまり、$cel{l}_{i,j}:=\mathrm{BlockSize}\times i\le x<\mathrm{BlockSize}\times (i+1),\mathrm{BlockSize}\times j\le y<\mathrm{BlockSize}\times (j+1)$ の領域として、$p$ と $q$ を結ぶ線分が通過するセルを列挙すればいい。セルの境界周りのコーナーケースが厄介で、ChatGPT に投げたけど、だめそう。通過していないセルを通過しているセルとして雑に扱っても問題ないので、妥協して実装したら 10 倍くらい速くなった。

搬入口につなげやすいように、パスの始点を x 座標が最小の分別器にして、終点を最も距離が短い処理装置のペアの近くに固定した。
始点・終点周りで修正不能な交差が発生しがちだったので、始点・終点につながる辺の距離を本来の 20 倍として扱ったり、初期解を貪欲で作ったりしてごまかす。

Day5

特に何もせず。

Day6

上位のスコアが想定を超えて伸びている。このままだとグリッドを完全に埋め込めても追いつけるか怪しい。マジか。とりあえず今組んでいるやつを提出してしまう。

まだまだ辺の交差が発生している。人力だったら直せるから頑張ればどうにかなるはずだけど、このままでは提出できない。しょうがないので、使用する分別器の割合を 95% → 90% → 75% → 60% → 40% の順に試せば、seed=0～99 では交差のない埋め込みが見つかるようなので、これで提出。

提出時 15 位。最終 50 位相当。

運が悪くて分別器使用率が 60% になっている。

上位に追いつくために、真面目にグラフの構築を考えるか。
今は処理装置の位置を均等にできると仮定しているけど、序盤はたくさんの種類のごみを分別するため難易度が高く、通過する分別器の数は多めにしたほうがいい。ただ、そもそもグラフの埋め込みにすらかなり苦戦しているのが現状で、処理装置の位置が意地悪なケースも多々ある中、どこまで処理装置の接続位置を制御できるのかは疑問。

特定の種類のごみについて、このごみをよく判別できる処理装置（出力 0 に流す確率が $0.2$ 以下または $0.8$ 以上）はそれなりにあるはず。これらを $k$ 個直列すると、特定の 1 種類のごみのみ $0.8^k$ の確率で通過させ、他のごみは $0.5^k$ の確率で通過させるコンポーネントが作れる。これを並列すれば良さげなグラフが作れそう。$k$ の値をいろいろ試すと $k=5$ くらいがちょうどいいみたい。
逆に、特定の 1 種類のごみのみ $0.2^k$ の確率で通過させ、他のごみは $0.5^k$ の確率で通過させるコンポーネントも作れる。こっちを並列させたグラフでは $k=3$ で十分みたい。$0.8^k$ と $0.5^k$ の確率の比に十分差がつくのが $k=5$ だったけど、$0.2^k$ と $0.5^k$ であれば $k=3$ で確率の比に十分差がつくということだと思う。その分通過させる確率が低くなるから、たくさん並列する必要があるが、スコアに大きな違いはない。$k$ が少なくて済むなら、それだけグリッドの幅が小さくできて小回りが利くので、処理装置の位置を考慮したルートを取りやすくなって嬉しい。
少なくとも、今考えているグラフを完璧に埋め込めたら、現時点の 1 位は余裕で越せそう。

Day7

ごみ 0 とそれ以外に分別する場面を想定して、2 種類のごみがあり、ひとつは分別器で (0.8, 0.2) の確率で分別でき、もうひとつは (0.5, 0.5) の確率で分別できるような状況で、できるだけ正確に分別できるようなグラフを焼きなましで作ってみたら、こんな感じのグラフが生成された。これまでのものと比較してかなりスコアがいい。

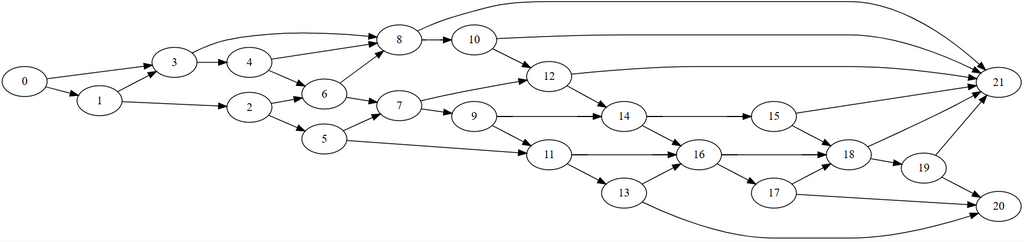
このまま平面に埋め込めそう。さすがに最大次数がもう少し小さくないと難しいかもしれないが。というか、グラフの構造ごと焼きなませばめちゃくちゃスコアが上がるのだとしたら、トポロジカル順を固定して接続先ごと焼きなませばかなり良くなる気がしてきた。ということで、グリッドの埋め込みのロジックを使い回して作ったジグザグで交差のない経路をトポロジカル順にして、分別器の割り当てと接続関係を同時に焼きなますやつを実装する。トポロジカル順が固定されていれば、辺が変わっても $O(\text{ごみの種類数})$ の差分計算は可能。

seed=1 のトポロジカル順はこんな感じになった。

差分更新の実装にてこずったが、15 位。最終 40 位相当。

Day8

時間を 10 倍にすればスコアが 1.7 倍くらい良くなるらしい。高速化します。
辺の候補はトポロジカル順が近い分別器 30 個くらいに限定しても問題なさそうだったので、これにより辺の候補の交差関係が事前に全列挙できるくらいになる。一度全列挙してしまえば、差分更新で現在の辺集合と交差しない辺をランダムに $O(1)$ で取得できる。ランダムに選んだときに交差しない確率が 5% くらいだったので、かなり高速になるはず。
つなげる先の頂点に入次数が少ない頂点を優先するようにした。 8% くらいよくなる。
処理装置の順序は、対応するごみが判別しやすい順につなぐのがいいと思うが、そもそも焼きなましが出力する解がごみを順番に判別している感じではないためどうしたものか。局所解なのか？ と思って雑に手動で禁止したら悪くなるから、そういうことではなさそう。
とりあえず、処理装置の割り当てを変更する近傍^[4]を追加したところ微増。
分別器の行き先を 2 つ同時に変更する近傍を入れた。

提出時 5 位。最終 20 位相当。

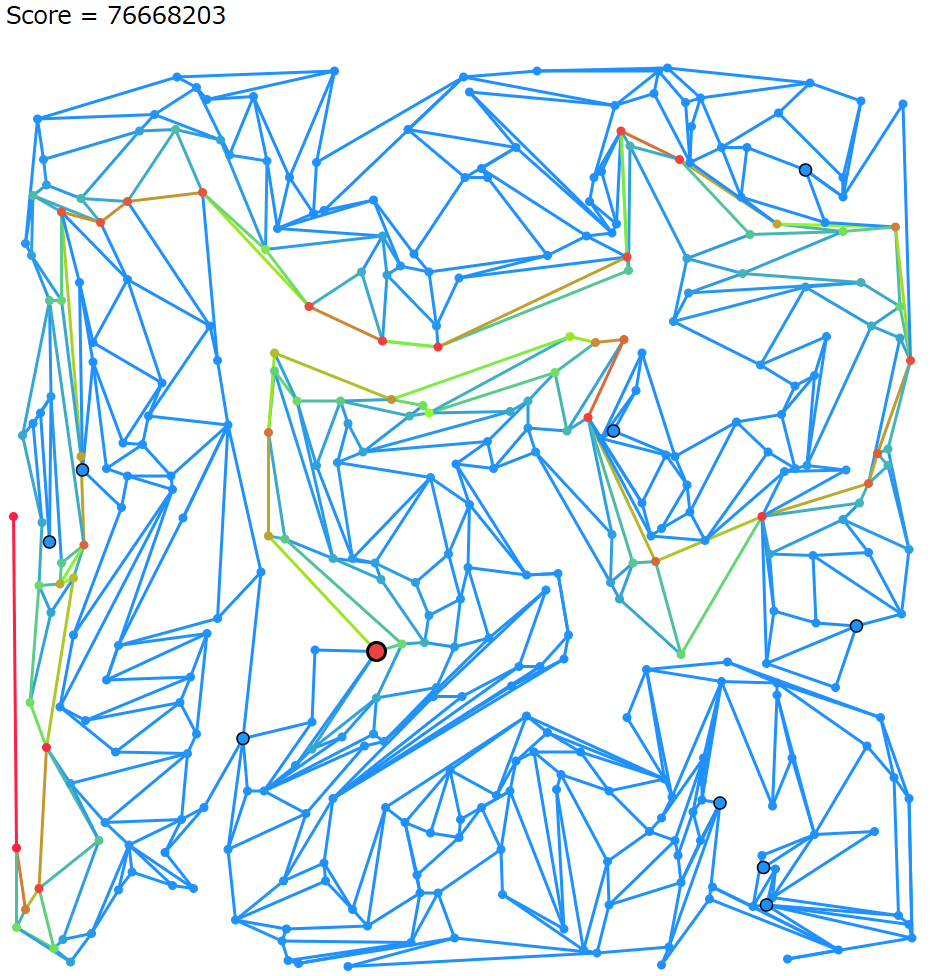
Day9

DP の SIMD による高速化を試したけどあまり速くならない？ そんな……（これは自分が SIMD に慣れておらず、ごみの種類数を 8 の倍数に揃えれば高速になったようです。）
辺を複数入れ替える近傍を試す。このうち、新たに有効になる辺を優先したり、パスを途切れさせない入れ替えをしたりなどが、高速化できればうまくいきそうだったので差分計算を頑張って実装する。複数変更されると、前からの DP と後ろからの DP による $O(\text{ごみの種類数})$ の差分計算はできないが、変更された頂点を含む最小の区間だけ DP すれば高速に計算できるはずなので気合で実装。
実装してみたが悪化。速度とのトレードオフ、難しい。焼きなまし側の伸びしろは少なくなってきたか。

現在の頂点に割り当てる分別器の種類を、現在のごみの種類の確率分布で最頻（最大確率）のごみをよく判別できる分別器から優先的に選ぶようにして、3 つランダムに試したときに最もスコアの良い分別器を採用するようにした。5% くらい良くなる。

提出時 5 位。最終 15 位相当。

たまたまこのケースでは前回の提出よりスコアが悪くなっているけど、平均的には良くなっている。

Day10

2 次元配列を 1 次元配列にしたり、グラフを CSR 形式にして 20% ほどの高速化。
ごみ搬入口に直接つなげる分別器を変える近傍の追加。
トポロジカル順を変更して辺をつなげる近傍も追加。詳しく説明すると、今の解法だと、事前に固定したトポロジカル順と矛盾のない辺しか考慮できていないが、 DAG を維持できるなら事前に固定したトポロジカル順を無視して辺をつなげてもいいことにする。そして、分別器 v からつなげる辺の行き先の候補を、事前に決めたトポロジカル順で v の 5 個前から 30 個先の分別器とするようにした。差分計算は辺を複数入れ替える近傍と同じように、変更された頂点を含む最小の区間だけ DP すれば高速に計算できる。この近傍がかなり効いて 10% くらい良くなる。
u → v の辺の向きを v → u に入れ替える近傍を試してみたが大して良くならなかった。
トポロジカル順を決めるときの焼きなましのスコアに、処理装置の位置のバランスを考慮したペナルティをつけたりしてみたが、手応えなし。
トポロジカル順が近い分別器だけでなく、距離が近い分別器間の辺も考慮できるようにしたが、こちらも改善なし。

提出時 5 位。最終 9 位相当。

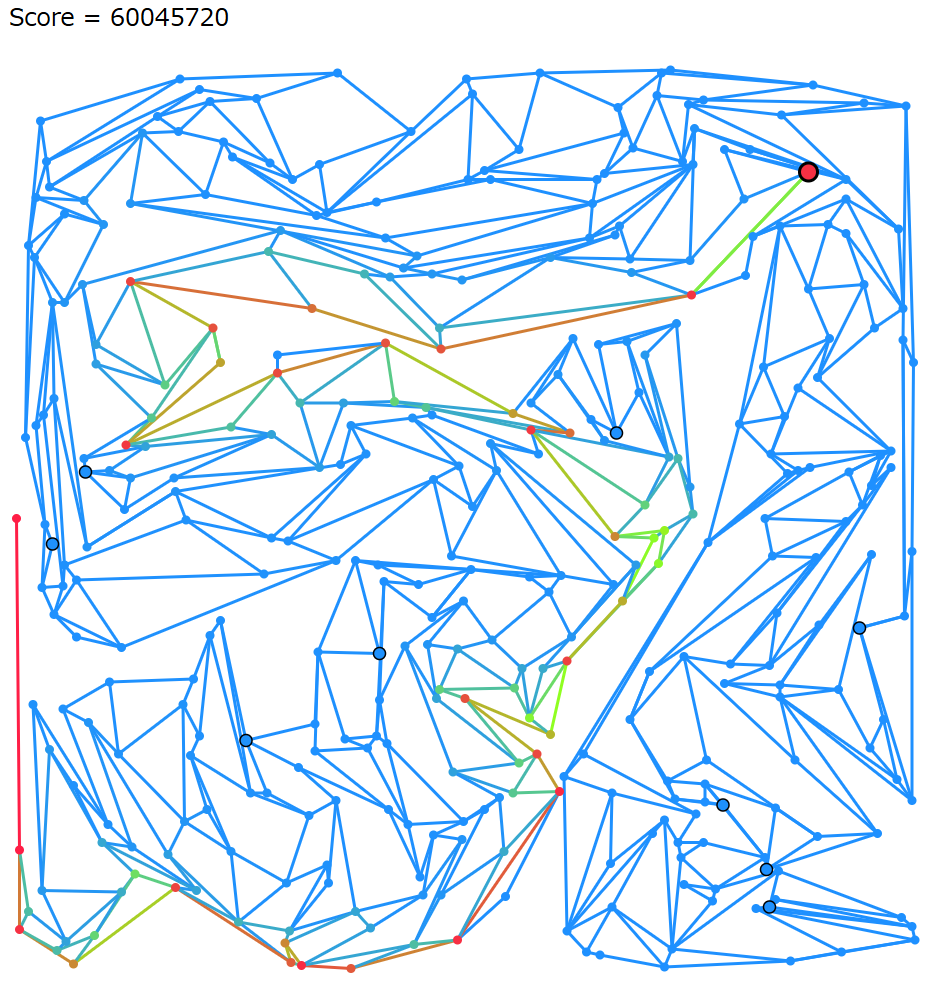
Day11

トポロジカル順の始点となる分別器を x 座標が最小の分別器ではなく、x 座標が小さい上位 30 の中から、最寄りの処理装置からの距離が最大の分別器を選ぶように変更して、5% くらい良くなる。
seed=32 などはこの変更で大幅に改善していて、

変更前	変更後

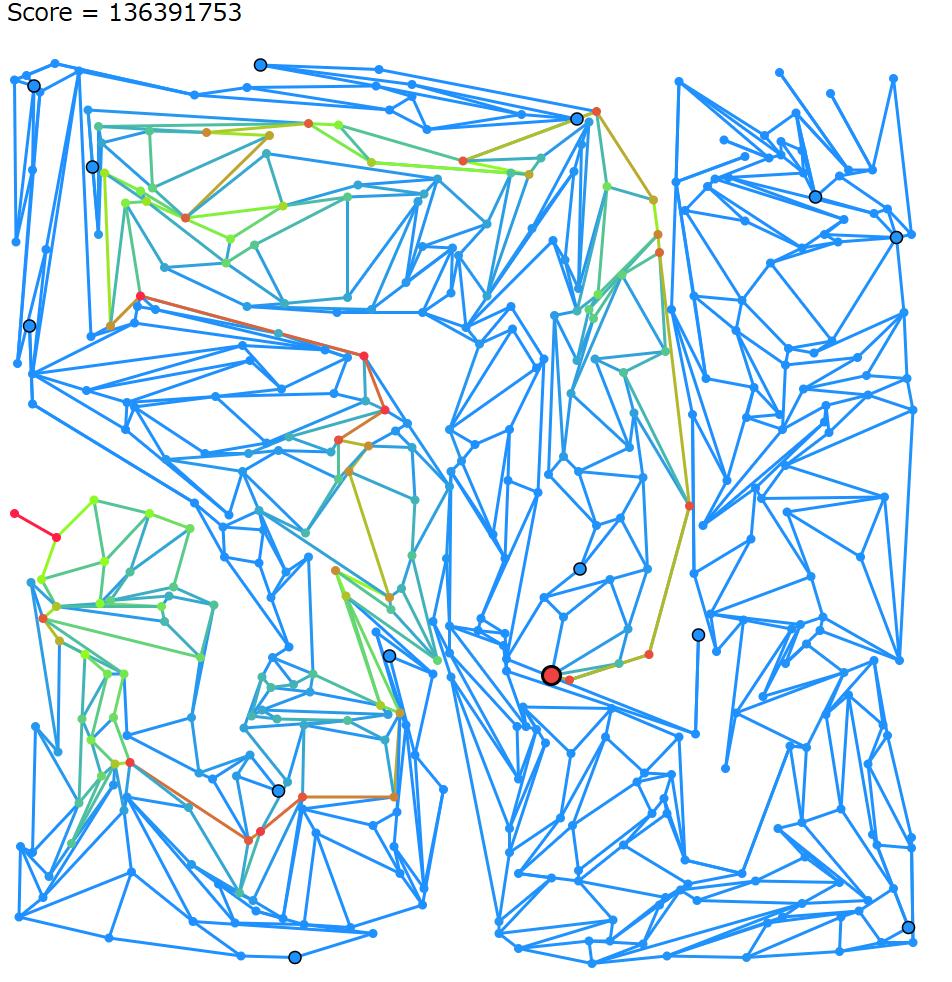最初に左上に突っ込んで爆死していたのがかなり改善されている。

やることがなくなってきたのでパラメータ調整を開始。現在の評価だと実行ごとの分散がひどくて数 % の改善が検知できないので、ローカルの評価体制を再整備する。20 ケースで評価していたのを 100 ケースに増やし、絶対スコアではなくローカルで 10 回解いたときのベストを使った相対スコアを使い、さらにトポロジカル順をファイルに書き出して固定した。パラメータをいじったり、これまで試したけど良し悪しが判断できなかったものを付けたり消したりして 7% 良くなる。
分別器が 300 個以下であれば 2 回解いて良かったほうを採用するようにして 0.5% の改善。

プレテスト 5 位、システムテスト 6 位。

終了後

この問題の重要な性質として「分別器の割り当ては貪欲に決めるだけでほとんど最適になる」というのがあったらしい。まったく気が付かなかったです。これを意識した探索が組めていれば、もっと良くなっていたかも。

X での解法ツイートを見る限りでは、

• 1 位 ： グラフの構造に大きな制約はなさそう
• 2 位 ： グラフの構造に大きな制約はなさそう
• 3 位 ： 二分木ベース
• 4 位 ： グラフの構造に大きな制約はなさそう
• 5 位 ： 二分木ベース
• 6 位 ： パスベース

という感じだった。

結局、自分は処理装置の位置を考慮したルート取りがほとんどできず、始点・終点を良さげな位置に決め打つくらいしかできなかった。処理装置の位置を考慮したグラフ作成という観点なら二分木ベースのほうが筋が良さそう。詳細は知らないけど、二分木の賢い構築もあるらしい。

処理装置が偏っているケースだと、分別器を均等に処理装置に割り当てるのが焼きなましだと難しそうだと思ったものの、焼きなましが強いのか、そもそも均等に割り当てる重要度がそこまで高くないのか、真偽は不明だが、最上位はグラフの構造はほとんど焼きなましに任せたみたい。分別器の数も多いし、高速化も難しめな気がしたため、グラフの大きな構造くらいは決めたほうがいいと思っていたけど、そんなことはなかったらしい。このあたりの正確な判断はいつも難しいですね。序盤の実験で一応確認はしているつもりでも、自分の予想が正しいほうにバイアスがかかりがちです。

1 位の解法解説で紹介されていたのですが、焼きなましでは微小な確率を扱うことが難しいため、序盤は確率の対数和を評価に使うといいらしい。なるほど。
参考 ： AHC051解法紹介（eijirou）

ともあれ、考察も実装も難しい問題でしたが、面白かったです。
明日のブログリレーの担当は @Takeno_hito さん、 @sorane_yaduki さん、 @SAH123 さんです。楽しみですね。