無限遠まで並ぶD-manの図
そもそもの話
そもそもシェーダとは何のためにあるのか?といえば、実はこのサイトのように綺麗な画像を生成するものじゃありません。シェーダとは、3DのCGプログラミングをするとき、ポリゴンの表面をちょっとかっこよくするためのものです。普通ならのっぺりとしたポリゴンに光沢をつけてみたり、鏡っぽくして反射させてみたり、良くてももともとある画像を加工するというくらいのもので、ここで紹介するように画面全体のすべてのピクセルの色をシェーダだけで決めるものでは断じてありません。が、これはこれで面白いのでまぁいいです。
さて長い前置きはこのくらいにしまして、レイマーチングとは何かを説明していきます。
レイトレーシングの話
レイマーチングとは、レイトレーシングと呼ばれる3DCGの技法の1つです。レイトレーシング法とは、カメラからレイ(光線)を仮想的に飛ばし、光線にあたったものの色をディスプレイに塗るという技法です。
例えば3D空間上に、カメラがあったとします。
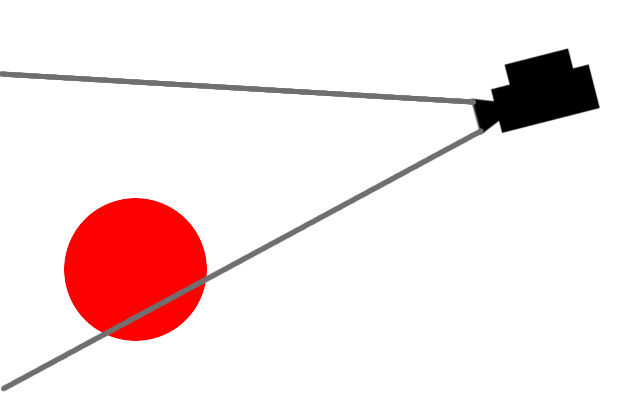
カメラは空間のどこかを向いており、カメラに写った3D空間がディスプレイに映しだされます。

話をわかりやすくするため、†ちょっと†だけ画像が粗いことにしましょう。

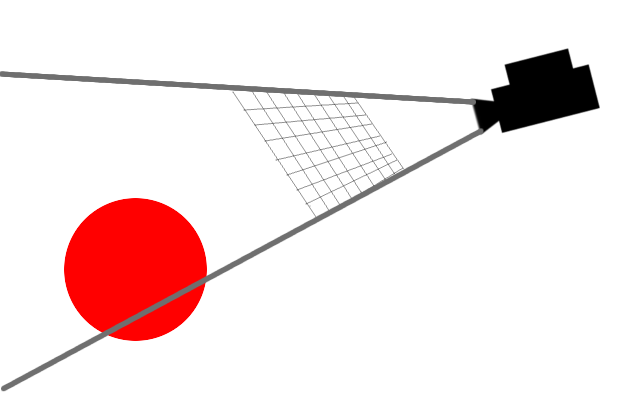
格子はピクセルです。こうなっていたとしたら、
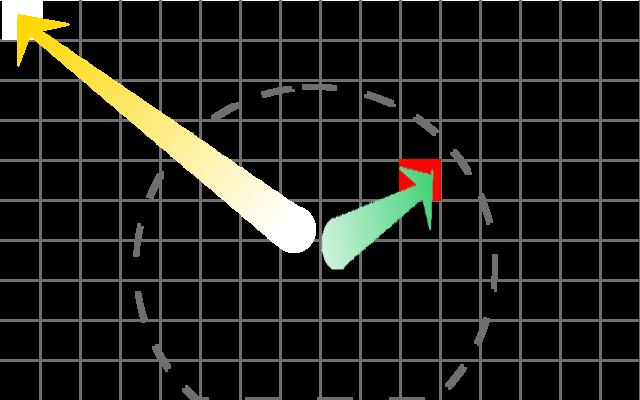
手前から奥に向かって、各ピクセルに対しレイを飛ばし、そのピクセルの色を順に決定していきます。現実の場合にはカメラから光線を飛ばすのではなく、カメラに向かって光線が飛んでくることになるわけですが、まぁ似たようなものです。
ここで問題となってくるのは「実際にどのように色を決定するか」です。もっと言えば、「あるレイを飛ばした時、そのレイは何に当たるのか」を決定することが一番の焦点となります。
単純に、レイに沿ってカメラからちょっとずつ進んでいき、ぶつかるかどうかを逐一判定するという方法(レイマーチングという)を考えてみます。
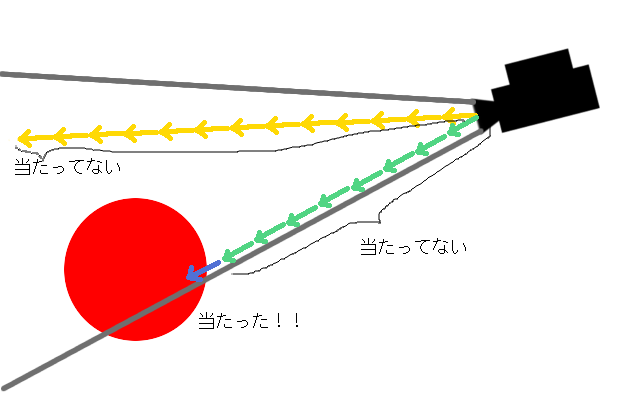
つまり、擬似コードとしてはこうなります。
pを現在の位置とする
p = カメラの位置;
while (true) {
pをちょっとだけレイのほうに進める;
if (pが物体とあたっているか?) return その物体の色;
}
このコードでは、「何にも当たらなかった場合」に無限ループになってしまうので、実際には適当な回数で打ち切ります。しかし、それによってある程度遠くのものは描けなくなります。もし遠くのものを描きたければ、ループ回数を増やすか、「pをちょっと進める」という部分の「ちょっと」を長くするかの二択になりますが、ループ回数を増やすとめちゃくちゃ重くなりますし、進む幅を長くすると、小さな物体を素通りしてしまったり不自然なジャギーが入ったりします。
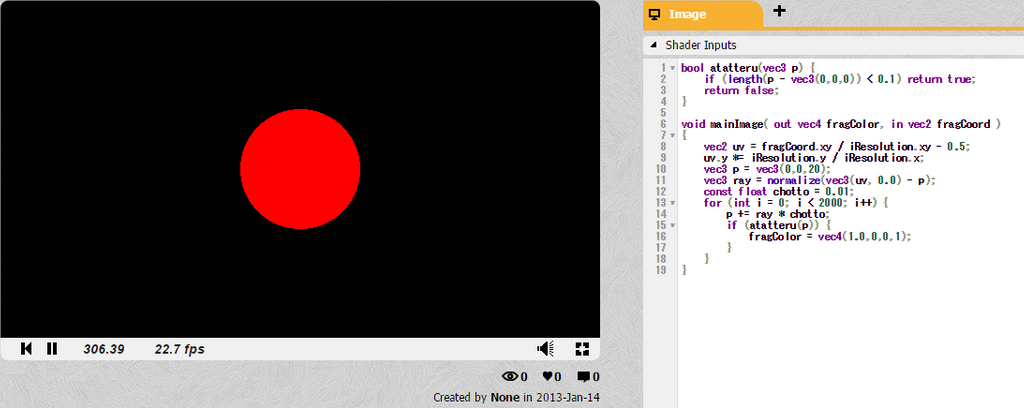
レイマーチングの例。こんなもんでもFPSが足りない。
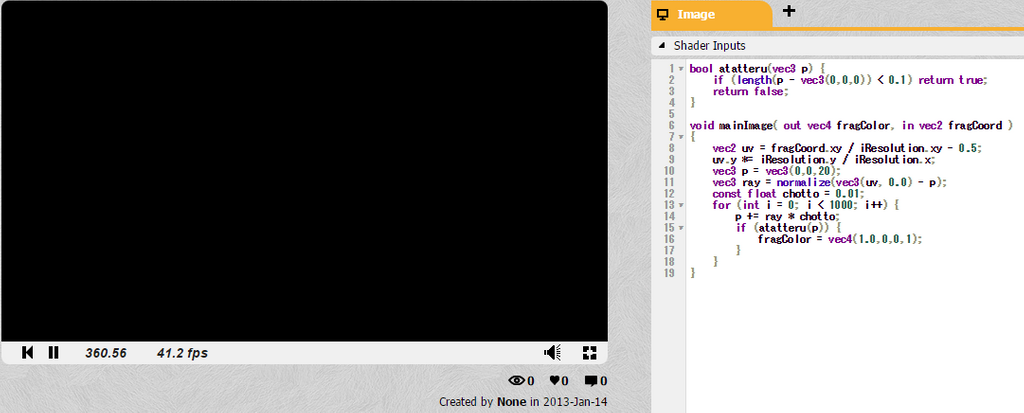
ループ回数を半分にしてみる。レイが遠くまで届かないため、何も映らなくなる。
レイマーチングと距離関数の話
上の方法でやってみて解決できなかった要求は、「そこそこの速さで」「綺麗に」「遠くの」物を描くことでした。この3つの要求を満たす、レイマーチングの亜種として、スフィアトレーシングというものがあります。先ほどの手法の問題点は、点が動く幅が一定だったことです。ちょっとずつしか動かないから無駄な時間を食ってしまうのです。もっと必要なぶんだけ、大胆に動いてしまいましょう。
「それができたら苦労はない」と思うでしょう。ですが、できるんです。その解決策は「x,y,z座標を引数とし、物体までの距離を返す関数」を作ることです。このような原点中心の球であれば、
float distanceSphere(vec3 p) {
return length(p) - 0.1;
}
といったかんじです。length(vec3)は組み込みの関数で、ベクトルの長さを返すものです。length(p)で原点からの距離をとり、そこから0.1引くことで、原点から距離0.1のところでは球とpとの距離は0,原点から距離0.2のときは球とpとの距離は0.1に...となり、ちゃんと球の表面との距離がとれます。球はめちゃめちゃ簡単ですが、工夫すれば直方体、円錐、球など様々な図形の距離関数を書くことができます。
このような距離関数を定義してやり、擬似コードを次のように変更します。
pを現在の位置とする
p = カメラの位置;
while (true) {
dを現在のpと物体との距離とする。;
pをdだけレイのほうに進める;
if (dがある程度小さいか?) return その物体の色;
}
dを計算する際に距離関数を用います。これがスフィアトレーシングです。
これを見て疑問を抱く方もいるかと思います。つまり、「これって物体が複数あったらどうするのか?」というものです。実はこれも解決できます。例えば、上の例では原点中心の半径0.1の球が1つだけでしたが、(0.1,0,0)中心の半径0.1の円と(-0.1,0,0)中心の半径0.05の円があったら、距離関数を次のように変更します。
float dist1(vec3 p) {
return length(p - vec3(0.1,0,0)) - 0.1;
}
float dist2(vec3 p) {
return length(p - vec3(-0.1,0,0)) - 0.05;
}
float distAll(vec3 p) {
return min(dist1(p), dist2(p));
}
min(float,float)は組み込み関数で、2つの引数のうち小さい方を返す関数です。簡単に言いますと、2つ以上の距離関数(でできる図形)を合成したければ、それらの最小値をとればよいということです。どうしてそれでいいのかといえば、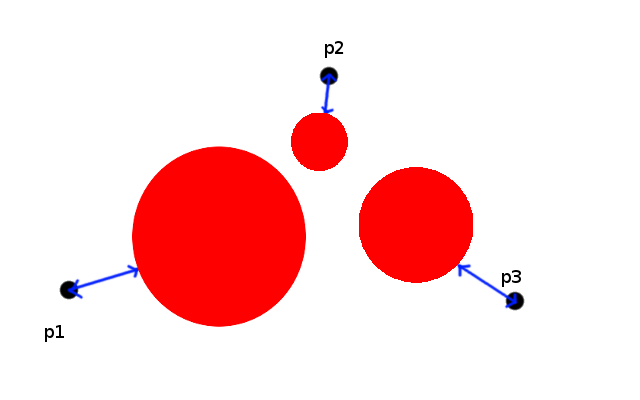
二次元の絵です
上のようにp1,p2,p3から赤い図形までの距離は、それぞれ青い矢印の長さとなります。図を見れば明らかなとおり、「点とある図形との距離」とは「点とある図形との最小距離」のことです。つまり、遠いやつなんてどうでもいいのです。一番近いものについてだけ考えればよいので、すべての距離のminを考えればよいということになるわけです。さて、このように距離関数を定義してやると、上に書いた擬似コードによりレイが図形と衝突するかどうかがわかります。
次のような状況を考えてみましょう。
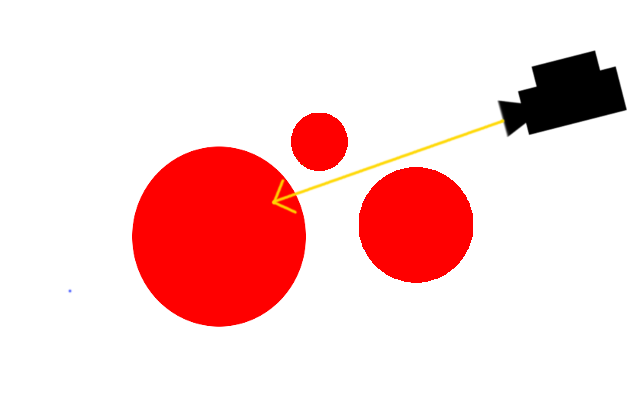
このようなレイが図形と衝突するかを判定したいとします。
まず最初、カメラ(の先端)から図形への距離は、図の黄色い円の半径にあたります。そのため、半径ぶんだけ前に進みます。
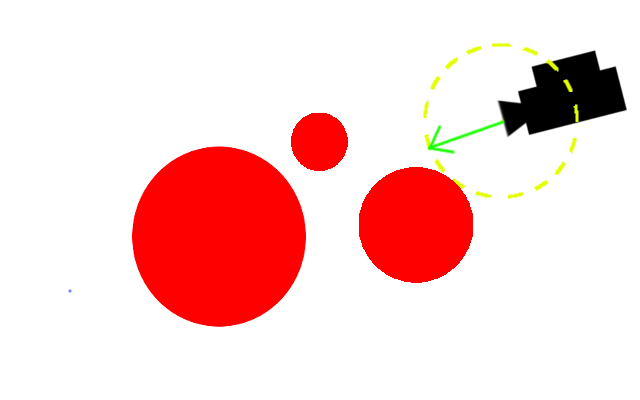
距離を測る→進むを繰り返していきます。衝突する場合には最終的に距離が0に近づいていくので、一定以上近づいたら終了とします。
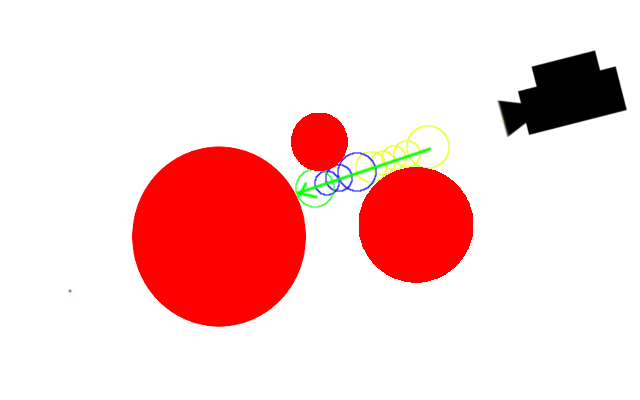
レイが衝突しない場合は、うまい具合に無限遠に飛び去っていきます。
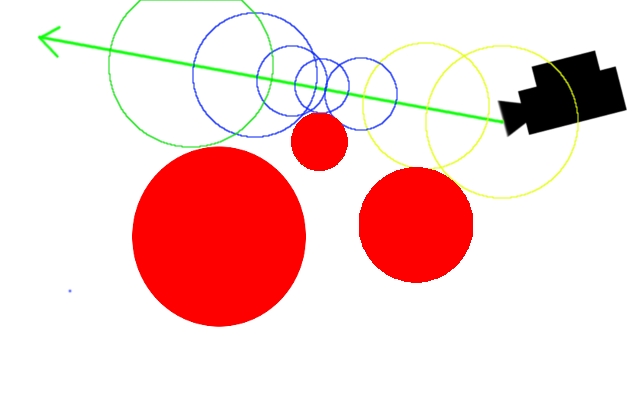
とまぁこんな具合にしてやると、レイマーチングが幾分か高速に行われます。特に、レイが物体に衝突しないときスフィアトレーシングは絶大な効果を発揮します。上の図のとおり、レイが物体に当たらず素通りするときは一度は進むときの刻み幅が小さくなりますが、ある場所を超えると急速に遠くへ行ってしまいます。そのため、「一定以上遠くへ行ったら終了」としておけば処理を格段に軽くすることができます。
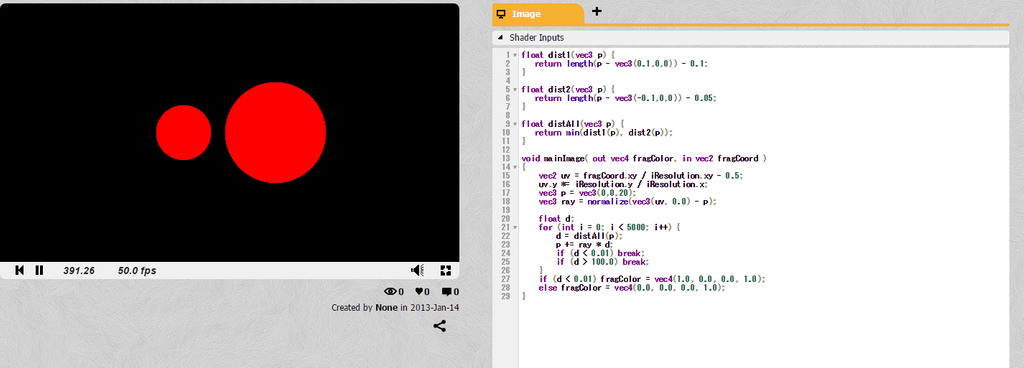
50FPS。はやい(確信)。
次回は色々な距離関数の紹介や、その応用について話していきます。
