Combinatorial Easing : 動かし方を分解する

こんにちはphi16です。traPの内部wikiに書いた記事をなんとなく公開することにしました。Easingの話です。

Easingとは、物をふわっと動かす動かし方のことです。
ぐいーんって動かしたり、もにょーんって動かしたり、ぽよぽよって動かしたり、いろいろあります。
基本的にこれは関数で指定されるのですが、種類もまぁいろいろあるし、実装方法もいろいろだし、自分で1から考えるのが難しい部分も結構あります。
というわけで、私の作ったEasing処理の書き方・作り方を書いていきます。
ソースコードはJS。

一般的な実装

Web系だと色々サイトは有るんですけどね・・・

これらに載っている方法を使うだけでは更に複雑なEasingを作ることはできません。ちゃんと理解しないと。
とりあえず色々見ると気持ちはわかるとおもいます。

EasingはEasing Functionというもので指定されています。これは何か、というと :

開始点と移動量を指定して
移動にかかる時間を指定して
Easing発動からの現在の時間を指定する

と、「現在の場所」を返してくれるというものです。なんかその辺のサイトは4引数取っていることが多いですね :

t : 現在時間 (time,実数)
b : 開始地点 (begin,実数)
c : 移動量 (change,実数)
d : 必要時間 (duration,実数)
返り値は現在地点 (実数)

例えばこんなのがあります :


function easeInQuad(t, b, c, d){
t /= d;
return c*t*t + b;
};

これは等加速度で目標まで行くやつですね。段々はやくなる。

さて。

Easing Functionの本質 (引数編)

本当に必要なEasing Functionは何なんでしょうね。使うときは4引数とってもいいとおもいますけど動かし方自体にそれはいらないとおもうわけです。

例えば「d」いらないですよね？tを元々 $[0, 1]$ でとるようにしてしまえば最初からt/dを渡せば良い話です。
また、実は「b,c」もいりません。だってb=0, c=1の場合を返すEasingを作っておけば、その返り値rをつかってr*c+bと表せるからです。線形性。

というわけで本当にEasing Functionに必要な引数はtのみであることがわかります。即ち、 $[0, 1]$ の実数を受け取って(だいたい) $[0, 1]$ の実数を返す関数です。
今まで通りに使いたければこんな関数をつくれば良いでしょう :


function ease(f){
return function(t, b, c, d){
return f(t/d)*c+b;
};
}
function inQuad(t){
return t*t;
}

これを使えば、easeInQuad(t,b,c,d) は ease(inQuad)(t,b,c,d) と書けます。Easingの本質であるinQuad関数は非常に簡潔になりました。

ということで、「1つの関数で万能Easingにする」のではなく「関数を組み合わせてEasing」する、ということで Combinatorial Easing という名前をつけました。コンビネータ指向っていうんかなぁ？あまり聞かない。

こうすることで様々な利点があります :

Easingの種類を増やしやすい (b,c,dに気を遣う必要がなくなった)
引数の組み合わせをカスタマイズしやすい
ease(f)(t,b,c,d)の他にも
ease(f)(t,p,q,d)のように「始点と移動量」ではなく「始点と終点」を指定したり
ease(f)(d)(p,q)(t)のように引数を分割してpos = ease(f)(d)(p,q);とすればpos(t)で値がとれたり
ease(f).frame(d).fromTo(p,q)(t)とかease(f).seconds(d).beginChange(b,c)(t)のように、可読性を上げながら機能を追加したり
Easing Function自体を改造したり : というのを次に書きますが。

Easing Functionの本質 (In/Out編)

Easing Functionには大まかに3種類あります。

in : 段々速くなる。最初の速度が0。
out : 段々遅くなる。最後の速度が0。
inout : 段々速くなって段々遅くなる。最初も最後も速度は0。

例えばquad系には次の3つがあります。


function inQuad(t){
return t*t;
}
function outQuad(t){
return -t*(t-2);
}
function inOutQuad(t){
if(t<0.5)return 2*t*t;
else return -2*t*t+4*t-1;
}

こんな感じ。(http://easings.net/ja より)

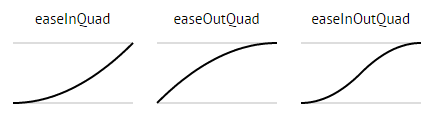
一応補足すると3つどれもf(0)=0, f(1)=1を満たし、またin系はf'(0)=0、out系はf'(1)=0を満たすはずです。

さてさて。

気づく人は多いとおもうんですけど、outはinを180度ひっくり返した形です。数式で表せば $o u t (t) = 1 - i n (1 - t)$ です。さらに、inoutは最初の半分をin、残りをoutとしてくっつけた形です。数式で表せば $i n o u t (t) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ \frac{i n ( 2 t )}{2} \frac{o u t ( 2 t - 1 ) + 1}{2} i f t \leq \frac{1}{2} o t h e r w i s e .$ となります。

つまり、inの定義さえあれば他は導出できるということです。なら分離しちゃおうね。

次のようにin用のEasing Functionを作成します。


function quad(t){
return t*t;
}

これからin,out,inoutを導出する関数を作ります。


function In(f){
return f;
}
function Out(f){
return function(t){
return 1 - f(1-t);
};
}
function InOut(f){
return function(t){
if(t<0.5)return f(2*t)/2;
else 1 - f(2-2*x)/2;
};
}

あとは使うだけです。
ease(inQuad)(t,b,c,d)はease(In(quad))(t,b,c,d)と書けるようになりました。いいかんじ。

Easing集

まぁ欲しいのはこれですよね・・・でも今までの結果により、easeInをひたすら書けば十分ということになったので。ちょっと楽。
ばーっと書いちゃいますね。ちなみに大体はPoyoEngine (進捗どうですか？を作ったときの自作ゲームエンジン) のコードです。


e.linear = (x)=>x;
e.smooth = (x)=>x*x*(3-x)/2;
e.quad = (x)=>x*x;
e.cubic = (x)=>x*x*x;
e.quart = (x)=>x*x*x*x;
e.quint = (x)=>x*x*x*x*x;
e.sine = (x)=>1-Math.cos(x*Math.PI/2);
e.circ = (x)=>1-Math.sqrt(Math.max(0,1-x*x));
e.exp = (x)=>Math.pow(2,-(1-x)*10);
e.back = (x)=>x*x*(2.70158*x-1.70158);
e.softBack = (x)=>x*x*(2*x-1);
e.elastic = (x)=>56*x*x*x*x*x-105*x*x*x*x+60*x*x*x-10*x*x;
e.bounce = (x)=>{
var pow2, bounce = 4;
while ( x < ( ( pow2 = Math.pow( 2, --bounce ) ) - 1 ) / 11 ) {}
return 1 / Math.pow( 4, 3 - bounce ) - 7.5625 * Math.pow( ( pow2 * 3 - 2 ) / 22 - x, 2 );
};

これらはとりあえず私が使うから書いているもので、新しいEasingを追加するのは簡単だとおもいます。
まぁ、これを元に「使いやすいインターフェース」をつくるのはみなさん次第ってことで。

さらなる合成

まだこれは実験段階なのですけど。Easingをさらに抽象化するとおもしろいかなとおもって。

例えば


forM [0..9] $ \i -> ease 0 100 $ sequent i 10 0.3 . easeInOut . cubic

とかやると

まぁ、こういう特殊なEasingもすぐつくれるかも、みたいな。これが元々のCombinatorial Easingなんですけど、ちゃんと紹介するのはまた今度で。

まとめ

easeInQuad を ease/inQuad に、そして ease/in/quad にするという話でした。
Generics, templateのような、元々は「データ構造×型」だったものを「データ構造+型」にするような感覚と近いですね。
既存のEasingはあまりにも冗長すぎるとおもうわけです。

わざわざb,c,dを取る理由自体よくわからないですけど・・・まぁそういう世界なのでしょうか。
In/Out/InOutの分離も誰か先駆者が居てもおかしくないとおもうんですけど・・・先例がいれば教えていただきたいです。

まぁまぁ、Easingを導入するとまぁいろいろ幅がひろがるのでよいです。
でもやみくもに導入するのではなく綺麗な？コードにできると良いなとおもいます。

ジャンプみたいな加速度的動きはquad系で出来たりするし、簡単なアニメーションを全てEasingで済ますのもありかもとかおもってたり。

というわけで部内wikiのコピペでした。他にも技術系の記事をいろんな人が(自主的に)書いてたりします。知見を集めていこうな。
ちょうど今Easingをいっぱいつかったゲームをつくっています。完成したら技術報告もかこうかなとおもっているのでおたのしみに。