こんにちはphi16です。趣味の話をします。ゲーム開発に全く関係はないです。

導入

ここに、丸があります。


と言っても実は丸ではなく、円柱の断面なんですけど。


こいつをAって呼ぶことにしますね。


さて、また違う色の丸があります。


これもまた同様。


これをBって呼びます。

ここに、また不思議なものがあります。


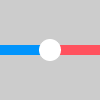
これは、左から右に、「円柱Aを円柱Bに変換する装置」です。言い方を変えると「パイプAから流れてきた物体をパイプBに流せるように変換する装置」です。

ここに、「円柱Bを円柱Cに変換する装置」があれば――


この2つの装置を繋いで、「円柱Aを円柱Cに変換する装置」にすることができます。


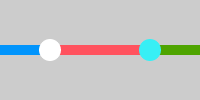
いいですね？


また、装置はいくらでも使うことができます。例えば、「AをAにする装置」があったとしたら――

いっぱいつなげて、また別の「AをAにする装置」を作ることができます。


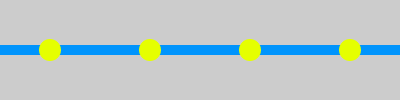
ちなみに、どうやって装置が変換しているのかは知りません。本当はAが整数を表していて、この黄色の変換装置は「1足す」ことを表しているかもしれません。でもそんなことは考えないことにするのです。

装置の変換

今までは点と線で考えていましたけど、実はこれも線と面の断面でした。


とすると、「変換装置の変換」を考えられるようになります。・・・具体例で捉えると難しいでしょう？


こんな「AからBの装置」があったなら――


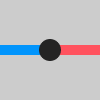
下から上に、「白の装置」を「黒の装置」に変換する装置があったりするのです。(必ず在るわけではない。)

勿論どうやって変換するのかは知りません。でもそんなものがある、というのが前提なのです。


さっきと同じように、この装置は合成ができます。「黒の装置」を「橙の装置」にする装置があったなら――


これらを合成して、「白の装置」を「橙の装置」にする装置を作れます。





さらにちょっと変わったことに、「BをCにする装置」を付け加えることもできます。


ちょっと見難いですけど、これは上にある空色の装置の本来の姿を右につなげたものです。




そして、ここに「BをCにする装置」がもうひとつあり――


さらに「空色の装置」を「紫の装置」に変換する装置があるなら――


先程の合成された装置にまた合成することができます。


ここで重要なのは、装置の上下の順番は入れ替えてもいいことになっている、ということです。

この3つは全部同じものを表していることになっているのです。まぁ見た目的に、順番はどうでもよさそうな感じがします。だって「AをBにする装置」の変換と「BをCにする装置」の変換は関係ないはずですから。


さて、結構こんがらがってきました。一度リセットしましょう。

装置の変換の変換装置

いまここにはAだけがあります。そして白と黒の「AをAに変換する装置」があります。


↑ これはAを一度白の装置に通してから黒の装置に通すような装置ですね。

そして青と赤、2つの「白の装置を黒の装置に変換する装置」があります。


そこで今回は、こんなものがあるとしてみます :

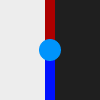
これは、「白の装置」を「黒の装置」に変換する装置としての「青の装置」を「赤の装置」に変換する装置、です。


もはやAの情報は見えなくなってしまいました。でもこれは見た目上の問題で、実はちゃんとAの情報は残っています。

**これもまた断面なのです。**Aは空間を表し、白と黒の装置は面で出来ています。青と赤の装置は線で出来ていて、空色の装置は点に相当します。がんばって描くとこんな感じです。

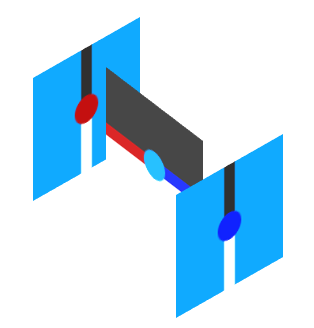
今まで何の話をしてきたかというと、「次元」の話なのです。「次元」の持つ構造について、単純なモデルを使って0次元から3次元まで軽く見てきたのです。これから細かく見ていきます。

A → Aの持つ構造

とりあえず、「AをAに変換する装置」に限った話をみていきましょう。今回はAは白色です。


桃色の装置をFとします。いま「AをAに変換する装置」はどれくらいの種類あるでしょうか？

まず、「装置を使わない」というのがあります。

そして、Fそのものがあり、またFにFをつなげたもの、もあります。


同様にFをいっぱいつなげたものも「AをAに変換する装置」ですが、逆に言えばある0を含む自然数nをつかって「n回Fをつなげたもの」という表現のできないようなものはあるでしょうか？

答えは「無い」、です。つまり今、「AをAに変換する装置」と自然数は綺麗に一対一対応します。(これは、1要素集合{F}から成る自由モノイド、と表現されます。)　まぁ数のことを考えたのは「どんなものができるかなー」ということを考えてもらうためで、特に意味はないです。

ちょっと考えてもらいたいのは、「もはやAについては考えてない」ということですね。今はFが主役です。なぜなら、Aはそれだけでは何も出来ないですが、Fは横につなげることができるのです！できることが多いほうが楽しいに決まっていますね。

さて、では「AをAに変換する装置」を「AをAに変換する装置」はどんなものがあるでしょうか。具体例を見てみましょう。


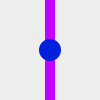
なるほど。いつもの感じですね。こんなのはどうでしょうか？ :


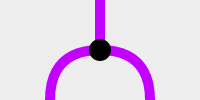
「FとFをつなげたもの」を「F」に変換する装置です。ありですね。


「無変換」を「F」に変換するのもありです。いろいろありますね。


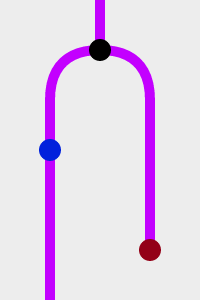
今までの装置を組み合わせてもまた新しい装置をつくれるはずです。いっぱいありそうですね。

さて、ではここではちょっとした「体系」を考えみましょう。

いまここにはAとF、そして黒の変換装置のみがあります。


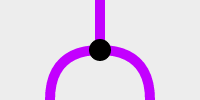
ここで次のような2つの変換装置を考えてみます。PとQとしましょう。



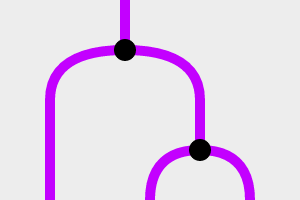
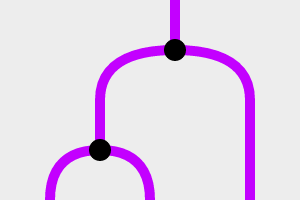
どちらも「Fを3つつなげたもの」を「F」に変換する装置のようです。ここでさらに、次の変換装置を与えます！


見た目からはわかりませんが、これは「PをQに変換する装置」です。ついでに「QをPに変換する装置」も作っておきます。

何ができるのでしょうか？ちょっと見ていきましょう。


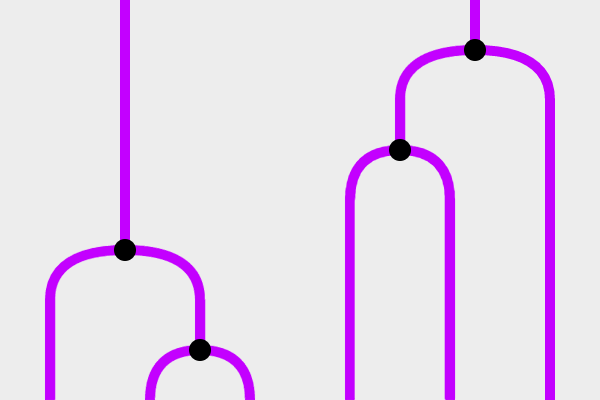
こんなのがあったとき、左下部分はPと一致し、右上部分はQと一致しています。ここで、**左下部分に「PをQに変換する装置」をつなげてみます。**すると、

なるほど変換されました。うん。この変換は3次元上で起こっているので平面上では経過はわからないですね。でも特に困ることはないです。

ついでに右上のQをPに変換してみました。なるほどこういうことができるようです。

で、これはなんなのか、ってことです。結論から言うと**「結合律」**です。 $x(yz)=(xy)z$ っていう、アレです。

Fは台集合、黒の変換装置は二項演算、そして水色の変換装置は結合律「そのもの」です。

いま、結合律を2回使うことで2つの変換装置系を変換しました。これは次のように表されます。


並んでいる黒線は今までの黒丸を下から並べたものです。まず下の2つの演算を結合律で変換し、上の2つの演算を結合律の逆(Q→P)で変換しました。この過程もまたこのように装置として表現されます。そしてこれは、先程の2つの変換装置系の「同値性」を示していることに他なりません。A→BとB→Aがあって可逆ならその2つは同じですよね。今回結合律は可逆なのでOKというわけです。

このようにこの世界では、 集合 → 演算 → 法則 → 証明 を、全て基本は同じだが次元が違う変換装置として扱うことができます。全ての概念は変換装置なのです。

これは単位元です。なにもないところから単位元を拾ってくる。そして単位律を与えます :


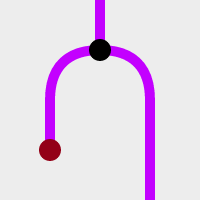
この2つの同値性を示すのがこれです :


赤演算と黒演算が、無くなって恒等写像になる、ということを表しています。

これでモノイドが表現できました(片方)。このように数学の証明などを全て「装置の変換」で扱ってみよう、というのが、この体系です。
長くなってしまったのでとりあえず終わろうとおもいます。次回(あるの？)ではさらなる次元の構造を見つつ、簡単な自然数の演算や、群の逆元が対合であることを示してみようとおもいます。

元ネタ

Globular というものがあります。出てきた図は大体これで作ったものです。詳細はここ。

一応扱いは「証明支援系」です。CoqとかAgdaのアレです。要は命題を書いて、証明を書くためのツールですね。Globularは汎用目的ではなく、実は圏論のある一分野のための証明ツールです。

圏論は対象や射を扱う分野ですが、圏の射としての函手、函手の射としての自然変換などを扱います。そしてさらに自然変換の射を・・・と、どんどん次元をあげていく理論があるのです。そしてその中でも単純なものとして、今回のような体系が成立しています。

ちなみにこのVisualizationに興味を持った方はString Diagramで調べると良いとおもいます。私が作った某プログラミング言語っぽいやつもこれに影響されて出来ています。


この体系は、単純なものであれば函数の表現もできるので、State MonadのMonad則の証明を作れたりします。


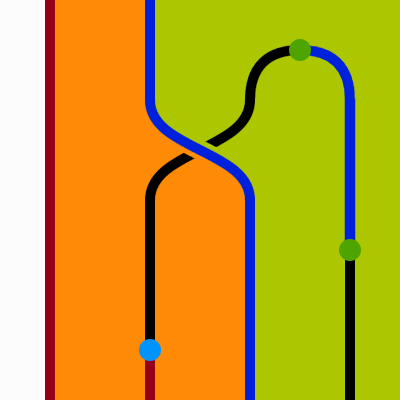
これはreturn a >>= f ≡ f aの証明なんですけど、まぁ見てもわかんないのはそれはそうです(何故ならそれぞれの函数の表現を書いていないのですから)

まぁ、こういうのがあるんだよーっていう紹介みたいなものでした。たのしいよ。