競プロをやるメリット

新歓ブログリレー7日目の記事です。
競プロが何なのか、始め方や精進の仕方は以下の記事を読むと良いでしょう。

競プロをやるとどんな良いことがあるのかを独断と偏見で列挙してみました。

データ構造の理解が深まる

データ構造を知っていますか。僕は知っています。スタックやキューなんかの構造化されたデータの集まりのことです。データ構造というのはそれだけ知っていても意味がなくて、具体的な問題に適用することで初めて効果を発揮するものです。

例えば、要素数Nのある集合に対して

データの追加
与えられたデータがその集合に存在するかを求める

という操作を高速に行いたいとします。例えば{2, 3, 5, 7, 11, 13}という集合に対して以下のように操作すると

> 5は存在するか
> ある

> 4は存在するか
> ない

> 4を追加
> {2, 3, 4, 5, 7, 11, 13}

> 4は存在するか
> ある

という風になります。

最初の操作では集合の中で5があるかを求めます。人間がこれをやるのは簡単ですが、コンピュータにこれを指示するにはどうすれば良いでしょうか。データがばらばらに並んでいる状態では結局はソートするかそれに相当する操作を挟む必要があるでしょう。そこでデータは予めソートされているとします。前から順番に調べていくこともできますが、二分探索というアルゴリズムで $lo g N$ に比例する計算時間で実行することができます。 $x$ があるかを求めるには、まず真ん中の要素にアクセスして、 $x$ がそれより小さければ前半を探索、大きければ後半を探索します。辞書で単語を探すときに真ん中のページを開いて、次に前半または後半の真ん中のページを開いて、という風に徐々に探索範囲を狭めていくやり方をしていた人も多いかもしれません。それと全く同じです。

3番目の操作で{2, 3, 5, 7, 11, 13}に4を追加して{2, 3, 4, 5, 7, 11, 13}としました。人間がこれをやるのは簡単ですが、コンピュータにこれを指示するにはどうすれば良いでしょうか。C++の固定長配列やvectorならデータはメモリ上でも連続的に並びます。しかしデータを追加する度にそれより後方にあるデータを全て移動させるのは効率的ではありません。前方にあるデータを移動させるときも同様です。しかしデータが昇順に並ぶ保証が無ければ二分探索が使えなくなるように見えます。

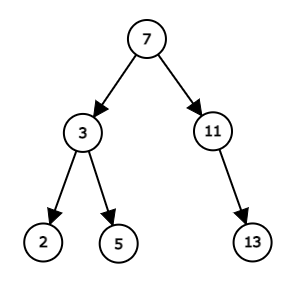
そこでデータが以下のような平衡二分木というものになっているとします。平衡というのは二分木のノードが縦ではなく横に広がっていることです。AからBへ矢印が引かれているときAからBへアクセスできることを表します。データ間の関係を抽象的に表したものなのでデータのメモリ上の配置とは無関係です。左の矢印の先にあるデータは元のデータより小さく、右の矢印の先にあるデータは元のデータより大きくなっています。

二分木の一番上のノードから辿っていけば二分探索と同じことができます。ここでは解説しませんが、データを追加しても二分木の平衡を保つことができます。C++のsetなどは平衡二分木で実装されています。

アルゴリズムの理解が深まる

競プロの問題は答えが出れば良いというわけではありません。実行時間やメモリ使用量に関して制約があります。アルゴリズムを内容だけ理解するのではなく、実際に手を動かして実装してみることのメリットの一つは、計算機のリソースに対する感覚に敏感になれることです。与えられた時間/空間計算量の制約の中で、このアルゴリズムは使えるがこれは使えないとか、データ構造はどうすべきかなど、考えることは色々あります。「自分に作れないものは理解できない」^[1]って良い言葉がありますが、その通りだなあと思います。

リチャード・ファインマン ↩︎

難問が揃っている

大学で出される課題とは雰囲気が違うタイプの問題が大量に揃っているのは嬉しいです。

難問の例(↑易↓難)

https://atcoder.jp/contests/abc215/tasks/abc215_e 問題を読み取るのが難しいかも。
https://atcoder.jp/contests/abc215/tasks/abc215_f 素直に計算しようとすると時間に間に合いません。
https://atcoder.jp/contests/abc215/tasks/abc215_g 自分は解けません。
https://atcoder.jp/contests/abc215/tasks/abc215_h 自分は解けません。

レベルの高い環境

センター/共通テストは受験者が世代あたり半分弱で平均が6割というところです。AtCoderでは、参加する時点で既にバイアスがかかってますが、人数がレートに関して単調減少なので上位層に対して解像度が高いです。このような高いレベルの環境で自分がどの位置にいるか分かるのは面白いかもしれません。

AtCoderの色のランクに対する評価があるので貼っておきます。

社長の記事：やや古い
公式：途中

ちなみに

自分は今競プロやってないです(は？)

明日はUzakiさんの記事です。楽しみ～～