アルファベータ法を使ったボードゲームAIの簡単な作り方【AdC2021 3日目】

アドベントカレンダー2021 3日目の記事です。

記事を読んでくれてありがとうございます。21Bの @grkon です。この記事では、ボードゲーム(チェスとか将棋とかそういう類のやつ)のAIや評価関数をアルファベータ法というもので簡単にプログラムする方法を書いておこうかなと思います。

アルファベータ法って何するもの？というのは、まあ要はAIが効率的に先読みするための手段です。ボードゲームは5手先となれば10万個ぐらいの分岐があったりするのが普通なので、そんなの全部読み切れないよね、でもいい方法あるよ、という話です。

ボードゲームAIの仕組み

評価関数ってなに？

ボードゲームAIを作る際に最も重要になってくる概念が評価関数です。これは要は、盤面に対する点数です。簡単な例を載せます。これは僕が最近指したチェスの対局の場面です。

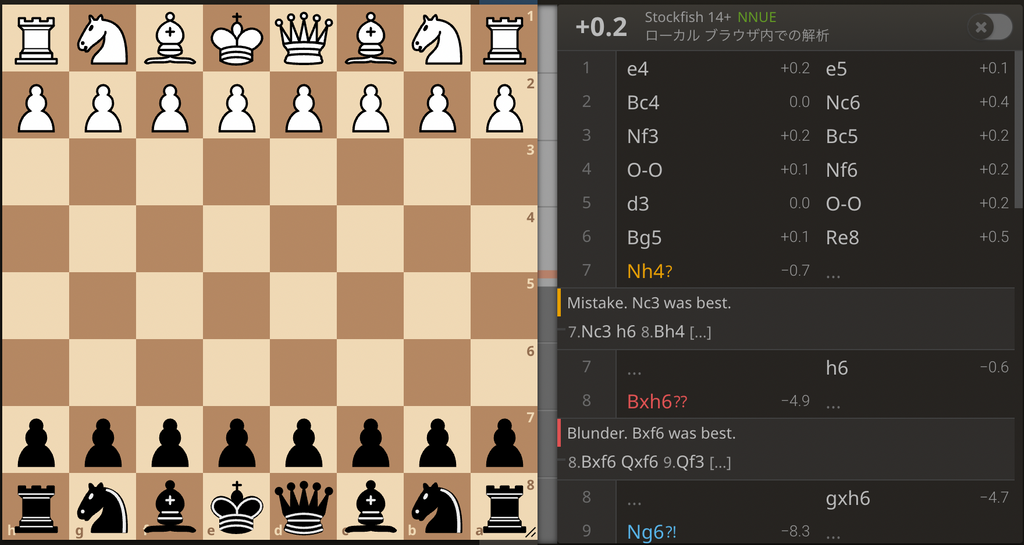
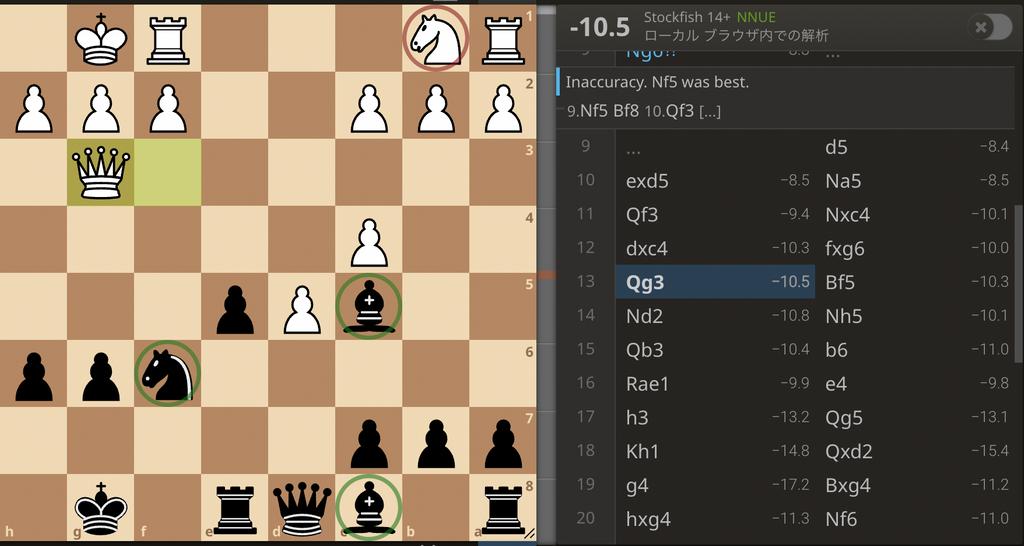
右上に書かれている $+ 0.2$ とか $- 10.5$ とか書いてあるやつが、評価関数の値です。これを盤面の評価値と言います。 $+$ とか $-$ とかの符号がついていますが、これはチェスや他のボードゲームでもよくある手法で、 $+$ では先手有利で $-$ では後手有利ということを指します。(ちなみに、チェスでは白先手です。)チェスでは最初は先手が若干有利と言われていて、だから $+ 0.2$ です。それに対して、2枚目では黒の駒の方が多いので、黒が有利です。だから、 $- 10.5$ です。そして、この絶対値である $0.2$ とか $10.5$ とかが、どれだけ有利か不利かということを表しています。

このように、どちらが有利かという意が込められた符号付きで、有利不利の差の大きさを計算するプログラムが評価関数なわけです。

かっこいいですね。

評価関数に基づいたAI

ボードゲームAIというのは、評価関数に従順に従ってくれる、評価関数の犬です。

かわいいですね。

つまり、次の手のうち、もっとも評価値がよくなるような手を指すわけです。まあこの手の選び方は単純で、次のありうる手の評価値を覗けば、一番良いものが1つ見つかるという手法ですね。

これがボドゲAIの簡単な全貌です。

評価関数の作り方

さて、次は評価関数をどうやって定義するかです。これは色々手法があると思いますが、自分のやっている手法を紹介します。これがおそらく一般的です(そうだと信じたいが...)。

一時的な評価関数を用意する
先読みするためのプログラムを用意する
読んだ手の一時的な評価関数の値から、現在の評価値を決める

プログラムとしてはこんな感じのがあります。

//これが一時的な評価関数
int temporary_evaluator(BANMEN b) {
    int evaluation;
    //計算させる
    return evaluation;
}

//これが先読みのためのプログラム(普通は再帰関数を使うと思う)
int evaluator_main(BANMEN b, その他必要な情報) {
    if (先読み続けるなら) {
        for (次の手候補) {
            //いろいろな操作
        }
        return evaluator_main(b.手を指す(最善手),　その他必要な情報2)
    } else {
        return temporary_evaluator(b);
    }
}

//これが評価関数
int evaluator(BANMEN b) {
    return evaluator_main(b, 初期情報);
}

// BANMEN は盤面の情報を含んだもの

先読みが入ってくるあたりでアルファベータ法が火を吹くわけですね。

一時的な評価関数について

アルファベータ法について説明する前に、一時的な評価って何すればいいの、という話をします。どうしたら有利不利を判断できるのかということですが、これは駒などの相互的な位置とか個数とかを目安にすると良いです。

たとえばチェスだったら、駒は多い方が強いから生存している駒にその種類ごとの点数を与えようとか。駒は中央にあった方が有利になりやすいから、中央にある駒の点数を1.2倍ぐらいしようとか。もちろん、勝利するときの評価値は爆上げしましょう。

こんな感じで、駒に点数をつけたり位置に点数をつけたりします。ここもセンスの見せ所なのですが、結構こいつがジレンマなんです。

先読みはしないが、多少先のことも考えた一時評価にする
先のことは考えず、速度を重視する

この2つを同時に達成するのは結構難しいです。速度を上げて先読みの回数を上げるのがベストですが、次の手を読むというのは、深度が1増加するだけで少なくとも10倍ぐらいの時間がかかるものです。僕はまだ評価関数ビギナーなので、多少先のことを考えた一時的な評価関数を用意しています。

まあそんなわけで、一時的な評価関数が用意できたら、早速先読みのプログラムをしていく必要があるわけです。ここでアルファベータ法が活躍します。

我らがアルファベータ法！仕組みとプログラムの組み方

アルファベータ法の基盤、ミニマックス法

アルファベータ法を説明する前に、この考え方の元となっているミニマックス法について知ってもらう必要があります。ミニマックス法は一番純粋無垢な先読みの考え方で、速度のことを無視すれば最強です。アルファベータ法は速度を改善したもので、システム的にはミニマックス法と同じことをしています。もっと最強ですね。

まずは図を見てもらいます。
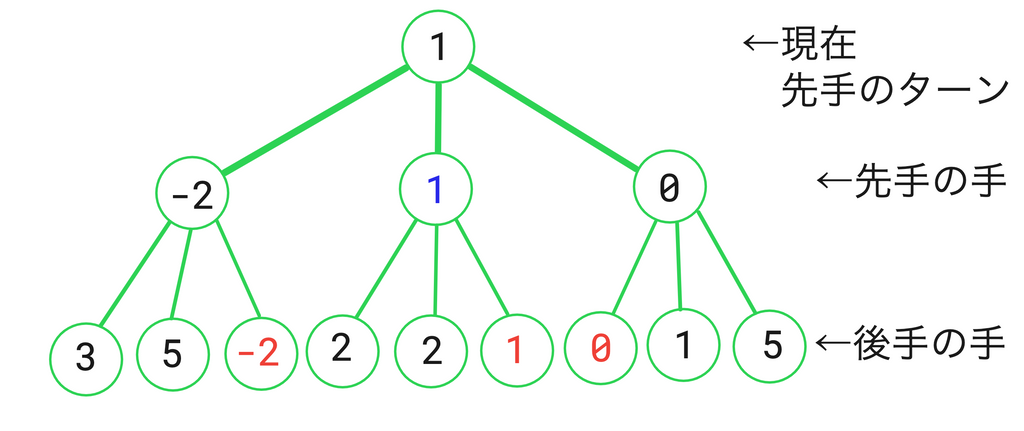
MiniMax法の例
これは、現在後手が指し終わった盤面で先手ターンの評価値を計算しようとしている場面です。各場面で指せる手は3手ずつあります。さて、ここでAIは”お互いが最善手を指した場合"について考えるわけです。つまり、先手ターンでは評価値が最大になるように、後手ターンでは評価値が最小になるように評価値に手を選ぶわけです。

$n$ 手先のことを深度 $n$ と言います。ノードと言ったりもします。
このプログラムの最大深度は2ということですね。深度2の部分を見てみましょう、ここは後手の候補手たちが並んでいます。深度2は最大深度なので、これ以上先読みしないということで、ここでは各候補手に一時的な評価関数で評価値を与えます。
さて、次は深度1の部分を見ましょう。深度1での評価値は、深度2の評価値のうち最善手の評価値をそのまま繰り越しています。そして各候補手に評価値が与えられて、またここでも最善手を深度0(現在)に繰り越すわけです。
そして、深度1で選ばれた最善手がAIの指す手となります。(過去の自分は、ここでもう一回候補手の評価値を計算させていました。アホですね。)

僕は数学とオブジェクト指向が大好きなので、手順を一般化します。

最大深度 $M$ を決める。
深度 $d = M$ の時は一時的な評価関数を使って評価値を計算
深度 $d < M$ の時は、深度 $d + 1$ の候補手の中から最善手を選ぶ
深度1で最善となる手をAIの手とする

以上です。プログラム的にはこう書きます。

int temporary_evaluator(BANMEN b) {
    int evalation;
    //計算
    return evaluation;
}

// ここが重要！
/*
    depth : 深度
    depth_max : 最大深度
    turn() : 先手が後手かを判断する関数(1なら先手-1なら後手)
    move(MOVE m) : 次の手を指す
    MOVE : 候補手を格納する型
    とでもしておきます。
*/
int evaluator_main(BANMEN b, int depth, int depth_max) {
    int max, temp, t;
    MOVE best_move;
    BANMEN b_temp;
    if (depth == depth_max) {
        //最大深度なら、一時的な評価関数の値を返す
        return temporary_evaluator(b);
    } else {
        //ターンで評価値の向きを揃える
        t = b.turn();
        b_temp = b;
        //最初の手を最善仮定しておく
        max = evaluator_main(b_temp.move(最初の手), depth + 1, depth_max);
        best_move = 最初の手;
        for (MOVE m = 候補手;;) {
            b_temp = b;
            temp = evaluator_main(b_temp.move(m), depth + 1, depth_max);
            //これまで探索した中の最善手よりも評価値が高かったら、これを最善手として登録
            if (t * max < t * temp) {
                best_move = m;
                max = temp;
            }
        }
        return max;
    }
    return 0;
}

int evaluator(BANMEN b) {
    int dm; //最大深度
    //最大深度を決めるプログラムなど
    return evaluator_main(b, 0, dm);
}

これでミニマックス法は完全攻略しました。

アルファベータ法のお気持ち

次はアルファベータ法ですが、こちらは仕組みが少し複雑になり、それを理解するのはそこまで難易度が高いわけではないですが、コードを書くときに少々混乱します。(僕みたいな、競プロやったことないer は混乱しやすいと思われ。)だから、ここでは混乱しないようにはっきりと実装法まで記します。

早速アルファベータ法について説明していきます。今回も先ほどと同じシチュエーションの図を見てもらいます。
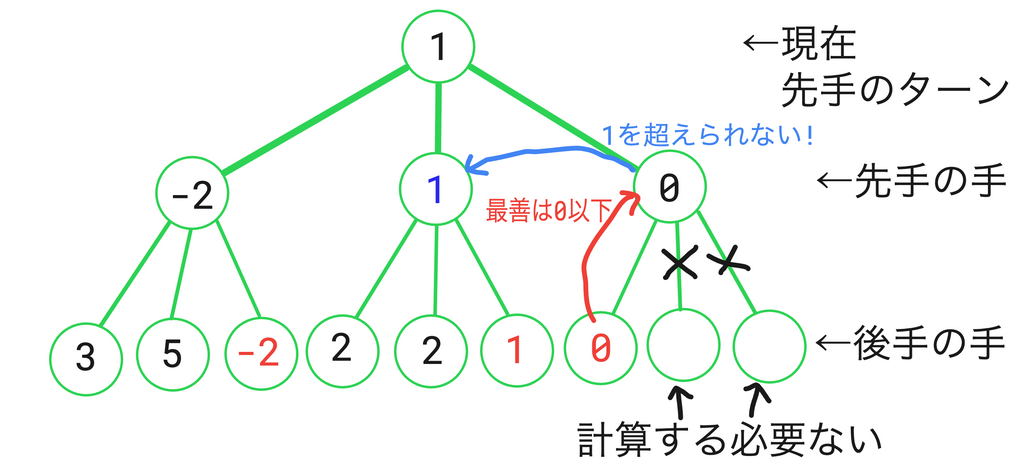
autodraw-2021_11_11-23_59_35

右側の2つが空欄ですね。これは計算する必要がなかったからしなかった候補手です。そしてその説明が図に書いてあります。もう少しわかりやすく説明します。

現在深度1の3つ目の候補手の評価値を計算しようと思っています。今のところ、深度1の最善の評価値は1です。だから、ここで1未満の評価値になるようであれば、今のところの最善手に負けてるわけだから、この候補手は最善にならないわけです。
それを踏まえて深度2の候補手を計算するわけですが、なんと評価値0が出てきてしまったではないですか！？後手は、出来るだけ評価値が小さいような手が最善になるわけですから、後手の最善手の評価値は少なくとも0以下になってしまうわけです。そうすると、もちろん深度1のこの候補手の評価値というのは0以下になる、すなわち1を超えられないわけです。だから、深度2の他の手を計算するまでもなくこの候補手を切り捨てたというわけです。

これがアルファベータ法の考え方です。これを何層も連ねて、アルファベータ法が完成するわけです。

美味しそうですね。

てか、アルファとかベータってなんだよ。って声がそろそろ聞こえてくる頃だと思います。
実はこのアルファとかベータというのは、切り捨てるき順となる値を保管する変数の名称です。アルファは、先手ターンで満たすべき条件、すなわちある深度での今まで計算した先手の候補手の中の最善手の評価値、ベータは、後手ターンで満たすべき条件、すなわちある深度での今まで計算後手の候補手の中の最善手の評価値を格納します。

アルファベータ法の具体的な説明

自分で書いていて何を言っているのかわからないので、ここでプログラムの一般的な実装方法を解説します。まずは先ほど同様手順の説明ですね。

はじめに説明するための設定をしておきます。 $(p_{1}, p_{2}, ..., p_{d})$ と表したら、 $d$ は現在の深度(現在の盤面を深度0としておく)であり、 $p_{k}$ は候補手が何番目かを指す数字、プログラムで言ったらインデックス(1-indexed)を表すことにします。これはどういうことかというと、最初の盤面 $()$ から、順に深度 $1$ では $p_{1}$ 番目の候補手, 深度 $2$ では $p_{2}$ 番目の候補手, ..., 深度 $d$ では $p_{d}$ 番目の候補手を指した先に行き着く分岐のことを指すということです。

ここで一つ重要な注意事項で、これが混乱しがちなのですが(僕は今でも正しいのか混乱してる)、アルファ、ベータの値は下の層に行く時は保存されます。そして、上の層へ行くときはその値は保存されません。下のプロセスでは、そのことについて書いていませんが、常にそうしていると考えてください。

$α = - \infty, β = \infty$ , 現在の位置を $()$ を探索させる
探索する命令を受けた候補手を $(p_{1}, ..., p_{d})$ とする。 $d$ が最大深度なら、一時的な評価関数を使って評価値を定める。そうでないなら、 $k = 1$ として3に進む
2 に戻り $(p_{1}, ..., p_{d}, k)$ を探索させて、その評価値 $e$ を得る
深度 $d$ が先手の候補手の場合は5, 深度 $d$ が後手の候補手の場合は6に進む
$e \geq β$ 　ならば、この候補手の評価値を $e$ とする。 $e > α$ の場合は、 $α$ に $e$ を代入する。 $k$ が最後尾までいってなければ、 $k$ の値を $1$ 増加させて3に戻る。そうでなければ、この候補手の評価値を $α$ とする
$e \leq α$ ならば、この候補手の評価値を $e$ とする。 $e < β$ の場合は、 $β$ に $e$ を代入する。 $k$ が最後尾までいってなければ、 $k$ の値を $1$ 増加させて3に戻る。そうでなければ、この候補手の評価値を $β$ とする

頑張って構成を考えたのですが、非常に複雑になりました。プログラムを見てもらった方がわかりやすそうですね。

int temporary_evaluator(BANMEN b) {
    //省く
}

int evaluator_main(BANMEN b, int depth, int depth_max, int alpha, int beta) 
{
    int e;
    MOVE best_move;
    BANMEN b_copy;
    if (depth == depth_max) {
        //最大深度なら、一時的な評価関数の値を返す
        return temporary_evaluator(b);
    } else {
        //ターンで評価値の向きを揃える
        t = b.turn();
        b_temp = b;
        //最初の手を最善仮定しておく
        for (MOVE m = 候補手;;) {
            b_temp = b;
            e = evaluator_main(b_temp.move(m), depth + 1, depth_max, alpha, beta);
            if (t == 1) {
                //現在探索している候補手が先手の場合
                if (e >= beta) {
                    //beta 以下にはなれないから切り捨て！
                    return e;
                } else if (e > alpha) {
                    //これが最善手となり、新しいalphaとして設定
                    alpha = e;
                }
            } else if (t == -1) {
                //現在探索している候補手が後手の場合
                if (e <= alpha) {
                    //alpha 以上にはなれないから切り捨て！
                    return e;
                } else if (e > beta) {
                    //これが最善手となり、新しいbetaとして設定
                    beta = e;
                }
            }
        }
    }
    if (t == 1) {
        return alpha;
    } else if (t == -1) {
        return beta;
    }
    return 0;
}

int evaluator(BANMEN b) {
    int dm;
    //最大深度を決めるプログラムなど
    return evaluator_main(b, 0, dm, -INT_MAX, INT_MAX);
}

プログラムにした方が複雑じゃないとは、なかなか面白いですね。

おわりに

以上でアルファベータ法の解説は終わりです。解説これだけなの、と思いましたか？結構わかりづらいですよね。このなんとも言い難い説明のしづらさは、アルファベータ法の特徴な気がします。

アルファベータ法を実践したい方は、ぜひいろいろなブログをまわってみてください。僕の解説は、理解の一部になっていただければ十分です。

ぜひ皆さんもボードゲームAI、作って見ましょう！楽しいよ！

明日はNapoliNさんの記事です！お楽しみに！