この記事は、新歓ブログリレー 2021, 50 日目の記事です。

はじめに

こんにちは、 @NNMochi と申します。
traP ではアルゴリズム班に所属し競技プログラミングをしていて、AtCoder のレートと AHC のレートの積は 2486169 です。

アルゴリズム班では AtCoder Beginner Contest などの解説会や、データ構造の講習会等が行われていたりしますが、今回は新歓ブログリレーという場を借りて、部内で行われている活動とは少し離れた AtCoder Heuristic Contest についてのお話をしようと思います。

私自身、Heuristic Contest をたくさんやってきたという訳ではないので拙い部分もあるかと思いますが、この記事を見ている人々にとって、
AtCoder Heuristic Contest に参加するハードルが少しでも低くなってくれれば幸いです(私を喜ばせたかったら是非参加してください)。

AtCoder ってなんですか？

AtCoder とは、「競技プログラミング」という、プログラムを書いて問題をいかに多く、そして速く解けるかを競い合うコンテストを提供するサービスです。
このブログの本質はここではないため詳細には話しませんが、知らない方はぜひこちらの記事を見て競技プログラミングを始めちゃいましょう。

AtCoder Heuristic Contest ってなんですか？

AtCoder は、大きく分けて二種類の問題を出題しています。第一に、AtCoder Beginner Contest(ABC と略されることが多いです)や AtCoder Regular Contest など、いわゆるよくある方のコンテストで出題される、最適解を制限時間内にもとめることができる問題です。

そしてもう一方が今回の主役である、AtCoder Heuristic Contest(以下 AHC と呼ぶ)などで出題される最適解を制限時間内にもとめることがとても難しい問題です。実際に、AHC 001 で出題された問題を見てみましょう。

問題概要 : たくさんの広告をスコアが大きくなるようにいい感じに置いてください。

こんな問題最適解を時間内に求めるにはあまりにも時間無いことは想像できると思います。ちなみに、これはダジャレです。
ダジャレかどうかはどうでもいいんですが、こういった最適解を求めることが困難な問題について、
スコアがなるべく高くなるようにすることが目標となります。

どう解けばいいの？

Heuristic Contest では、それ特有のアルゴリズムとして、山登り法や焼きなまし法、そしてビームサーチなどのアルゴリズムがあります。

これらは名前だけを聞くと難しそうに感じるかもしれませんが、山登り法は今ある解答に対していわゆる貪欲法を適用する事とほとんど同じであり、
ビームサーチはある状態から見る状態量を減らすことによって計算量を軽くした dp ととらえることができます。
また、焼きなまし法は少し特殊ですが、これらの貪欲法や dp では探索しきれなかった状態を探索する手段です。

つまり、これらのアルゴリズムは bit 全探索や union find のように実装がほとんど決まったものではなく、
問題に応じてどうやってこれらのテクニックを使い分けたり、適用するかが大事になります。

Heuristic Contest の流れの一例としては、問題やスコア関数からいい感じの性質をみつけて、最初にいい感じの初期解を設定し、
それを今あげた山登り法や焼きなまし法によってどんどん改善していく......といったように解答を制作していくものがあります。

実際、どのように考えながら問題を解けばいいのでしょうか？

Heuristic Contest では 100 人いれば 95 個くらい異なる解法がありますが一例として、AHC 001 の問題で私がどんな感じに解いたかを紹介します(pretest 485 億点の解答です)。

解法

初期解を考える

いい感じの初期解を設定するとはいったものの、いきなりいい感じの初期解を考えられるのは一部の慣れた人くらいでしょう。私は無理です。

ということで、まずは入出力の確認のためにも、正しい出力をし、かつ正の得点を得られる解法を考えます。

正の得点を得られる簡単な初期解を考える

希望スペース 1 * 1 のマスを各広告に与えれば、ぶつかることはないのでこれで正の得点を得ることができます。

これを提出すると、 pretest で 823,090 点を獲得することができます。うれしいね。なお、AHC においては、ペナルティを気にする必要は残り時間が多いうちはほとんどありません。

どんどん提出しましょう。また、問題によっては初期解で正の得点がなかなか取れないよ～ (´;ω;｀) なときもあります。

このような場合は貪欲法が有効だったりすることも多いので試してみましょう。

貪欲法のアプローチを考える

スコア関数を観察します。すると、ある長方形 i のスコアへの寄与分は、長方形の現在の面積を s[i], 目標面積を r[i] としたとき、
s[i] = r[i] となる時に最高になるということが分かります。

このことから、s[i] > r[i] となっている場合には、s[i] = r[i] のときと比べて他の広告が取れる場所の邪魔をしており、かつスコアも減少してしまっているため s[i] <= r[i] になるように縮めたほうが好ましいことが分かり、
同じように、長方形を伸ばした場合に s[i] > r[i] となる場合はあまり伸ばしたくないというお気持ちになります。

また、スコア関数のなかに二乗が入っているため、たとえば長方形 i, j に対して、 s[i] = 0.5 * r[i] と s[j] = 0.5 * r[j] が s[i] = 1.0 * r[i] と s[j] = 0.3 * r[j] がそれぞれ一つずつ存在するよりも望ましいため、現在の s[i] / r[i] が小さいものからどんどん伸ばしていくのがいい解法なのではないかなと考えます。

これを優先度付きキューなどを用いたり、目標とする割合をどんどん広くすることによって実現すると、pretest でおおよそ 450 億点を得ることができます。

これは長方形を伸ばす長さを変えてやれば比較的早く終了するので、あとはさらに伸ばす方向や長さについての乱択要素を入れて、時間ギリギリまで繰り返してスコアが最も高くなるものを出力すれば、pretest でおおよそ 460 億点を得ることができます。

この解をどんどん良くする

初期解でこれ以上良くする方法が浮かばなかったり、最低限書けて別のことがやりたいなと思ったら、
この初期解を改善していく作業に移りましょう。

とはいえ、改善するといってもどこを改善すればいいのかがなかなか分からないです。
そういうときは、ビジュアライザを用いて現在の解がどうなっていて、どういう風に改善できそうかを考えます。

今求めた解がどういう風になっているか？を確認する

ということで、ビジュアライザに現在作った解を入れてみましょう。えい！！

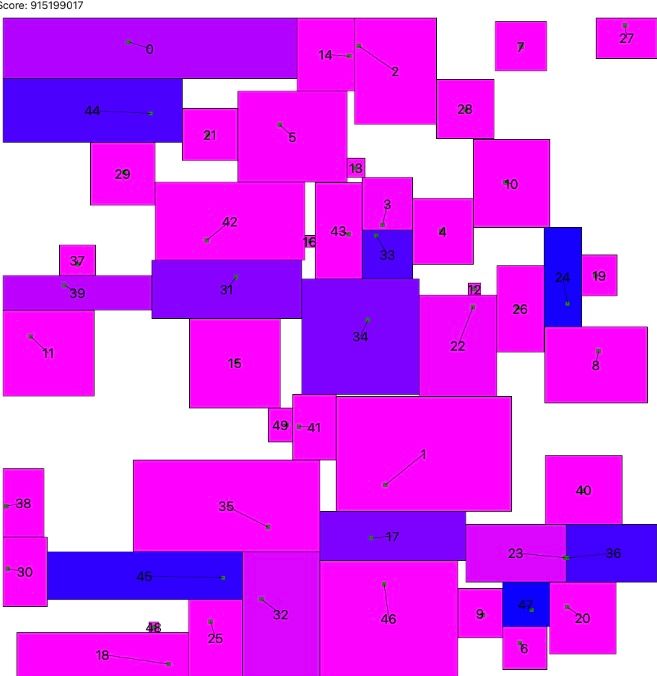
むーん、まだまだ小さい長方形がありますね......(青い長方形が面積が少なくて、ピンクに近づくほど面積が十分になっていきます)。
たとえば 35 番と 45 番の長方形なんかは、35 番の長方形を左上に移動してあげれば 45 番の長方形をもっと大きくできそうです。

ということで、長方形をスコアが悪くならないように移動させるという動作を加えてあげましょう。そうすると、どん！！！

青い長方形の数がかなり減って、さらに長方形が置かれていないスペースも目に見えて減りました、わーい(⋈◍＞◡＜◍)。✧♡！

また、伸ばす長さを適当に決めた場合、これを 0.1 秒行うときと、4.9 秒行うときでほとんどスコアが変わらないことがわかります。
そのため、時間いっぱい初期化解を決めて適当に移動させるということを繰り返す......ということを行うコードを書くことにします。

これを提出すると、pretest でおおよそ 470 億点を獲得することができます。なお、今回はこれがスコアが悪くならないようにどんどん変化させるという貪欲法のような考え方をしているコードであり、やったことは山登り方に分類されます。

次は何をしましょうか。47 番が青色なのが気になるところです。
これは 9 番の長方形を縦長にしたり 6 番の長方形を横長にするか、長方形がぶつかってしまうとしても無理やり拡張することを許すと解決できそうですね。前者は一見難しそうですが、実はそこそこうまくいくような方法があります。

スコアが悪くなるということを許容してみる

スコアがすぐに伸び悩んでいた原因は、今までしていたことが全て山登り法であったため、局所的な最適解に陥ってしまったためです。

単純化した図を用いて説明しましょう。説明を単純にするために、スコアが一変数関数であると仮定しています。

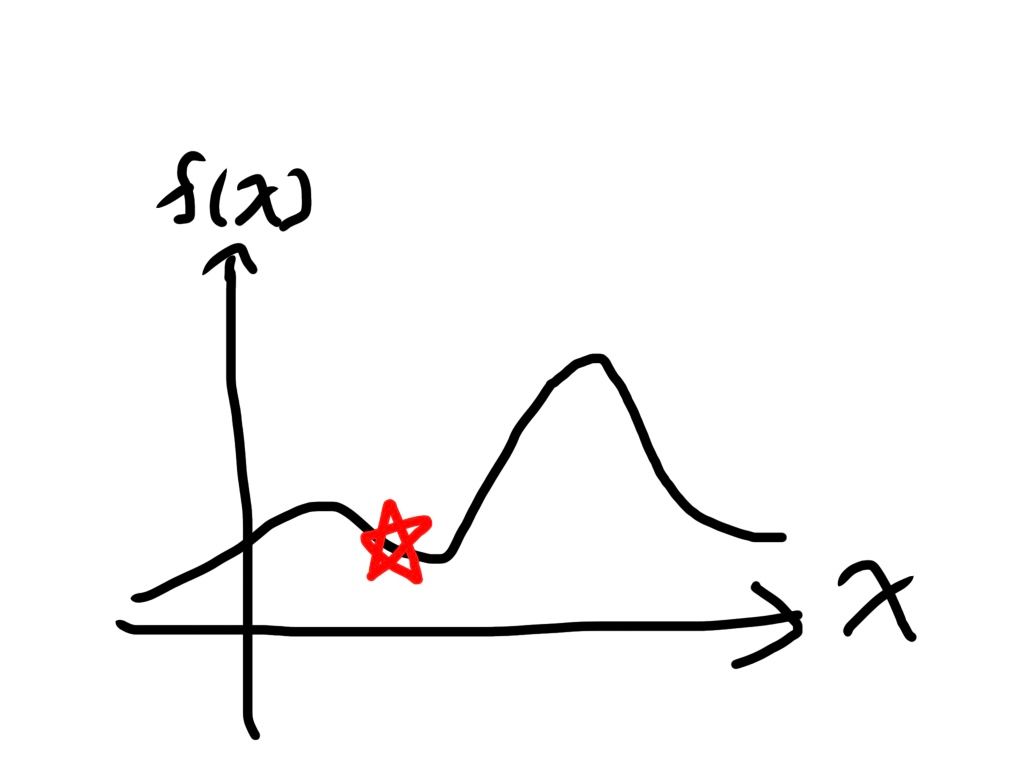
上のように、スコアが局所的に最も高いところを山と見立てます。山が 2 つある場合を考えて、今星印にいるとしたときに、スコアが高い方を目指しているので図の青線のように動きます。

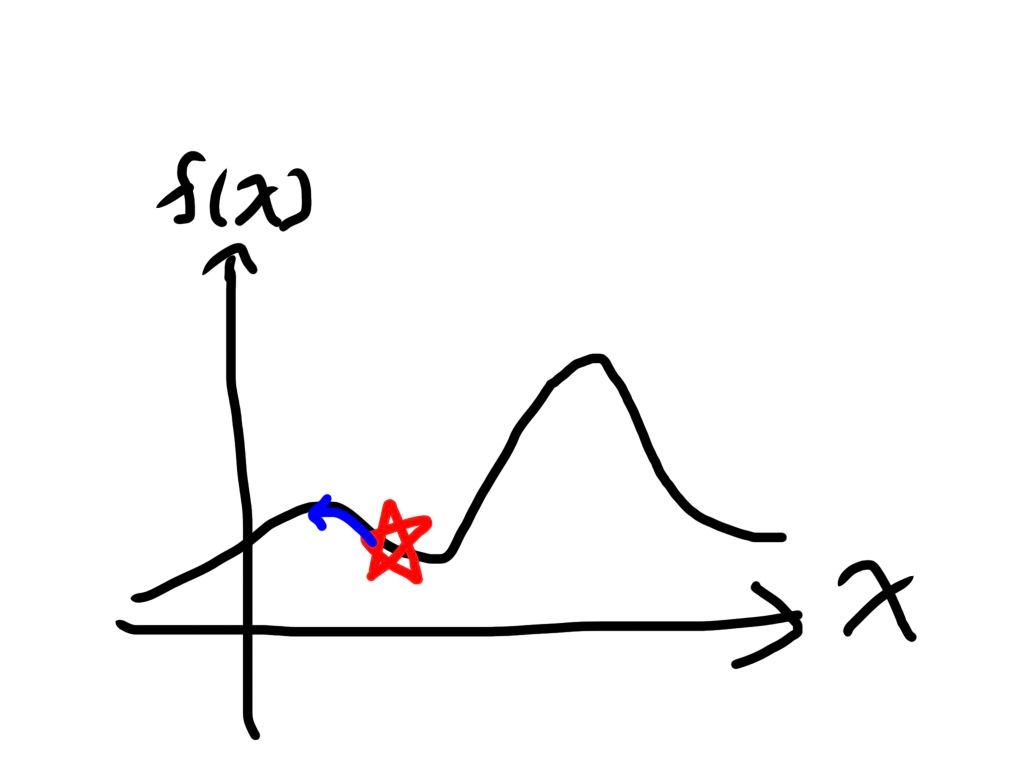
この山の頂点にたどり着いた時、移動する事はスコアを悪くすることになってしまうのでもう移動することはできません。
しかしながら、もう片方の山のほうが明らかにスコアが高いため、こちらの山を登るのが理想的なわけです。

もう片方の山を見るために、ときどきスコアが悪くなる変化も採用し、ある程度時間がたって全然良くならなかったら戻す......ということを行います。
これをすると図の緑色の線のように動くことがあって、最適解に移動できますし、逆方向の変化はほとんど起こらないのでうれしいです。

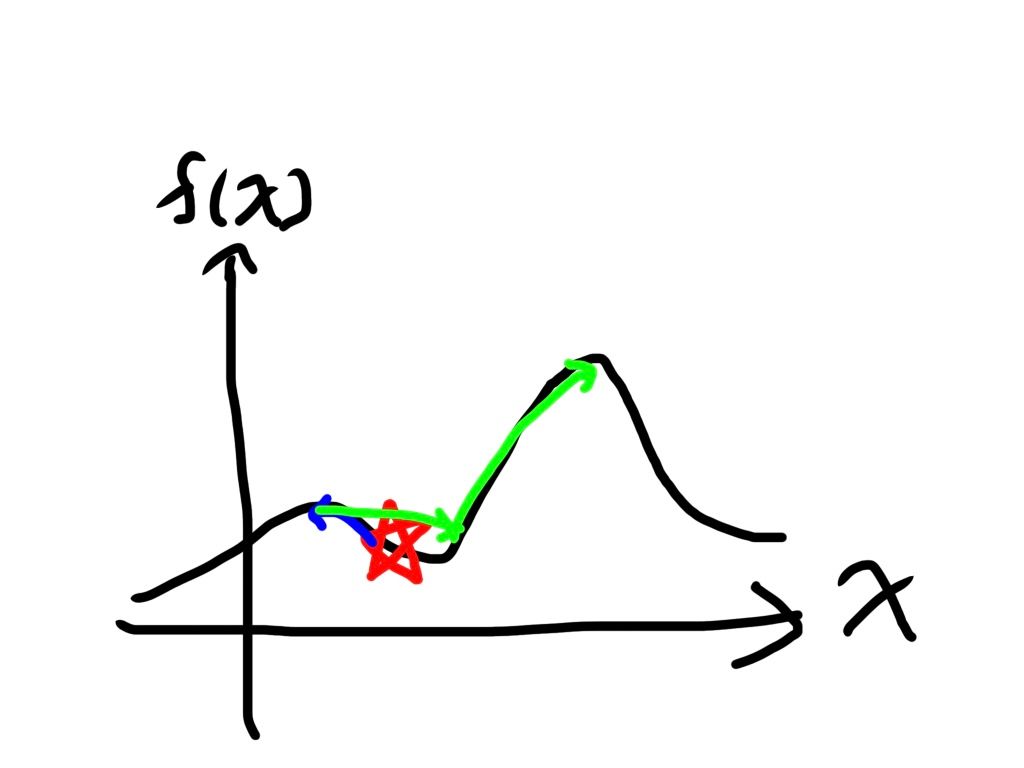
これが焼きなまし法の基本的な考え方で、焼きなまし法の場合、これに加えて終了時間に遠いほど悪くなる変化を採用しづらくすることによってより良い解を探索しやすくしています。

さて、本題に戻りますが、どうやって 47 番が青色なのを解消しましょうか。答えは簡単で、ランダムな長方形の面積を一旦 1 にしてしまって、またランダムに拡張するということをすれば良いのです。

隣り合うもの同士で改善するために、適当に生成した正方形と重なっている部分の面積を 1 にするという手法をとりながら、最適解を保存するというコードを提出すると、pretest でおおよそ 480 億点を獲得することができます。

最後に解を整える

またまたビジュアライザに現在の解を入れると、次のようになります。

なるほど、青い長方形はなくなりましたがまだまだ改善できそうなところはたくさんありますね（0, 1, 24, 45 など)。

前に長方形がぶつかってしまうとしても無理やり拡張することを許すと良くなりそうと書きましたが、これが実際に適用できそうな感じがしますね。
このように、今まで使用していないようなものを変数としてさらに山登りしてあげると、より良い解を得られる事が多いです。これを提出すると、pretest でおおよそ 485 億点を獲得することができます。これをビジュアライザに入れると、こんな感じになっています。

例えば 47 番を縮退した後に上に移動するなどとしてやればより良いスコアを獲得できそうですが、時間の都合上ここまでで終わります。
また、初期解を設定する時間をなくしたほうがなぜかスコアが高くなったので、それを提出したコードがこちらになります。

長いけど、結局何をしたんですか？

与えられた 1 * 1 のマスを離れないように長方形を拡大、平行移動、縮小するのを繰り返したます。そのあと、最後の 0.4 秒でスコアが良くなるならほかの長方形を押しのけて拡大するということをしました。

しかし、先にも上げたようにこれはあくまでも膨大にある解法のうちの一つであり、もっと良い解法もたくさん存在しますので、是非 #AHC001などで検索してみてください。

やってみて思ったこと

Heuristic Contest っぽいことをしなくてもそこそこの順位をとることができる

ここをいうためだけにこの記事を書いている可能性まであります。

Heuristic Contest とはいっても、初期解の決め方に成功すればそこそこいい成績をとれます。

実際、今回の初期解で獲得した 92 % のスコアを system test でとることができれば、492.5 位相当で 1441.5 performance(いわゆる水パフォの真ん中くらい)をとることができます。

AHC 002 においては私はいい初期解が思いつきませんでしたが、それが特に顕著だったらしいです。

また、ほとんど同じ理由で時間制限いっぱいまで回さなくてもいいことが多いから、Python 等の高速でない言語でもある程度は戦えます(最上位を目指すとなると厳しいですが)。

コードが長生きするので、数日後の自分や他人が見ても理解できるようなコードを書く

特に変数名を直観的に理解できるものにすることが大切です。
例えば、私はコンテスト中は問題文で与えられる一文字変数の X, Y, R などをそのまま用いたりしていましたが、
あまりにも難読でした(気になる人は私のコンテスト中最後の提出を見てください、実装量と相まって絶対に読みたくないコードがそこにはあります)。
これに気づき、コンテスト後半では優先度付きキューに prique_which_stock_score_and_index と名付けるなどとしましたが、これはさすがにやりすぎたかなと思いつつ、ここで頭が壊れることはなかったので効果は合ったかと思います。

いきなり難しいことをしようとしない

やろうとするとすぐバグります。ちょっとずつ積み上げていくのが無難です。

終盤以外は定数倍を改善するよりも、とにかく書きやすいコードを書く

要するに、いきなり難しいことをしようとしないということですね。

また、定数倍が悪いコードであっても、
定数倍が良いコードとの差分が分かれば手元で計算する時間を調整すればだいたいの点数が予想できるので、今やってることが本当に効果があるかどうかが確認しやすいのは大きいです。

ボトルネックとならないところでは計算量が多少多くなっても気にしない(ボトルネックとなっているところを改善すべき)

例えば一連の動作 : A -> B を時間いっぱいやることを考えます。

仮に現在、A をやるのに 1000 回計算する必要があって、B をやるのに 10000 回計算する必要があるとしましょう。

A を天才解法で計算回数を 1 回に落とせるとしても、B の計算回数が改善されなかったら一連の動作に 10001 回の計算が必要なのに対し、
B を少々の定数倍高速化で 5000 回に計算回数を落とせたとすると、一連の動作に必要な計算回数は 6000 回とこちらのほうが少なくなり、一連の動作を行える数が増えるためより良い解を獲得しやすくなります。

Rust 使ったほうがいいのかな

C++ では、バグがあるとすぐ segmentation fault して PC を投げたくなります。
segmentation fault の場合、どこにバグがあるかが全然分からないため実装量が多いコードだと丸半日一つのバグを探すのに使う......なんてこともあります。
これは悲しいので、どこにバグがあるかがわかりやすいと、ヒューリスティックコンテスト適性が高そうな Rust をインストールしましたが、Rust は難しく、AHC 002 は C++ で出て segmentation fault に一時間溶かしました。かなしいね。

点数がすごい大きくなって面白い

序盤で上位陣がどんどんスコアを伸ばしていくのは見ていてとても面白いです。

人生を大切に

人生がさき、競プロはあと。

最後に

現在参加している人はあまり多くなく、レベルが高すぎるとして敬遠されがちな Heuristic Contest ですが、
意外にもそこまで高度なアルゴリズムは要求されません。

また、問題が最適解を求める事がほとんど不可能であることだからこそ、試せることが多く、新しいことを試すことやコンテスト後に人の考え方を見ることもとても面白いです。

次の AHC は 5 月 22 日からの 200 時間コンテストと非常に長くなっていますが、毎日 2 時間程参加すれば十分にいろいろと試すことができると、Heuristic Contest ならではの魅力が非常に伝わりやすいコンテストになっております。
生活習慣を壊さない程度に、ぜひみなさんも参加してください！

明日の記事は @NABE さんです！お楽しみに！