この記事は、新歓ブログリレー2021 12日目の記事です。
みなさん、おはこんばにちは。
traPで活動しているpotato167です。
traPではアルゴリズム班に所属し、競技プログラミングに取り組んでいております。(ぜひ競プロを始めましょう)
今回は排他的論理和(以下xor)と言われるものについての紹介と、面白い使い方について述べていきたいと思います。
xorとは?
xorとはbit演算などにおいて片方が真で片方が偽のとき真となり、どちらも等しいときは偽となる演算のことです。
ex
| a | b | a xor b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
これを0以上の整数に拡張すると以下のようになります。
二進数標記した整数の各桁に対し、xor演算を行い、各桁で、その結果を返す演算。
例えば、
3 xor 5
=011 xor 101 = 110
= 6
のようになります。
基本的な性質
- 同じものどうしでxorをとると0になる (a xor a = 0)
- a xor b = 0 と、a=b は同値
- a xor 0 = a (単位元0)
- 足し算のように、交換法則や結合法則が成り立つ
組み合わせゲーム
以下のようなゲームは聞いたことがあると思います.
場に石がN個あります。この石を2人で順番に1個以上、4個以下とります。
最後の石をとった方が勝ちです。どちらが勝つでしょう
これはNが5で割り切れるなら後手の勝ち、割り切れないなら先手の勝ちです。
なぜなら、自分のターンの終わりに、場の石の数が5の倍数になるようにして返すと、相手の手に関係なく、次の自分のターンの終わりには、また4の倍数にすることができ,
最終的に0にすることができるからです。
これをたくさん並行して行うとどうなるでしょう?
場に石の山が4つあり、それぞれの山には石が、A,B,C,D個あります。2人は以下の操作を交互に繰り返します。
石が1個以上ある山を選び、その山から石1個以上、4個以下とります。(その山の石の数を超えてはいけない)
最後の石をとった方が勝ちです。どちらが勝つでしょう
この問題の答え実は、以下のようになります.
A,B,C,Dを5で割った余りをそれぞれa,b,c,dとすると、
a xor b xor c xor d =0
ならば、後手の勝ち、そうでなければ先手の勝ち。
なぜこうなるかについては説明を省きますが、xorの結果によってゲームの結果が最初からわかってしまいます。
組み合わせゲーム理論についてもっと知りたい人は以下のリンクを参考してみるといいです。
https://algo-logic.info/combinatorial-games/
数学の問題
4×4のマス目の各マスを赤、青、緑、黄のいずれか1色で塗る方法のうち、どの行と列についても次の3つの条件のうちいずれかをみたすものは何通りあるか。
・1色で4個のマスすべてを塗る。
・異なる2色でそれぞれ2個のマスを塗る。
・4色すべてでそれぞれ1個のマスを塗る。
ただし、回転や裏返しにより一致する塗り方も異なるものとして数える。
(第29回日本数学オリンピック予選 9問目)
例えば以下のようなものが考えられます。
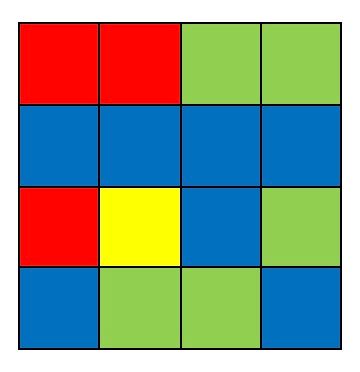
この問題の答えはどのようになるでしょうか?
下に解答があります。
実は左上の9個を決めた時点で答えが一意に定まります。
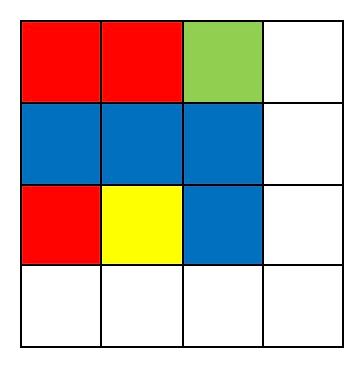
↓

また、左上の9個は任意に決めることができるので答えは4の9乗となります。
なぜこうなるのでしょう?
まず、各色に、0、1、2、3の数を振り分けます。すると、条件は以下のように言い換えられます。
各列、行のxor和が0になる
例えば、異なる色が2色で2個ずつ塗るとき、それぞれの色に振り当てられている数を、a、b、とすると、
a xor a xor b xor b
= (a xor a) xor (b xor b)
= 0 xor 0
= 0
となります。
よって、左上の9個を決めると、右下以外は自動的に埋まります。
例えば、赤に2、緑に3が振り分けられているとき、一番上の行の一番右に当てはまる数をXとすると、
2 xor 2 xor 3 xor X = 0
(2 xor 2 xor 3) xor X = 0
a xor b = 0 と a=b が同値なことから、
X = 2 xor 2 xor 3
X = 3
となり、緑となります。
右下のマスには必ず適切な色が存在するのでしょうか?
右下のマスは上3つのxor和と等しくなることが必要です。
このとき、左の3列、12個のxor和は0なので、右下のマスはそれ以外の15個のマスのxor和に等しいです。
上の3行12個のマスのxor和は0なので、右下のマスは、左の3つのxor和と等しいです。
よって、右下の数は一意に定まります。
(この計算に出てくる数のを2進数で表したときの桁数は最大で、2桁であり、0~3には対応する色が必ず存在します)
本番では答えだけ書けばよくて、この問題の答えは魅力的なもなので、
何で左上9個が決まれば答えが一意に定まるかわからなくても面白い問題ですが、
このように説明できると、この問題も、xorも、より面白く感じられると思います。
最後に
ここまで読んで頂きありがとうございました。
このxorについて詳しく知ったのは競プロを勉強していく過程でした。
競プロでも何でも、大学生に入って新しいことにチャレンジしてみると、自分が知らない世界が知れ、それがとても面白く感じることがあります。
ぜひ新しいことを始めてみてください
明日の担当者は@d_etteiu8383です。お楽しみに!