ごきげんよう。AdC2020 29日目のこの記事では、SATによる当たり判定について紹介します。頑張って書いたつもりではありますが、ガバやわかりにくい点などたくさんあるかもしれません。悪しからず。

SATとは

SATはSeparating Axis Theoremの略称であり、2つの凸な図形同士が重なっていないとき、2つの図形の間に直線を引くことができるというものです。

Wikipediaを適当に読んだところではHyperplane separation theorem（分離超平面定理）の応用であるように見えます。

参考：https://ja.wikipedia.org/wiki/分離超平面定理

今回はこれを用いて実際に当たり判定を実装します。例で示すコードはProcessing(Java)のものですが、ほとんどの言語で同様に実装できるかと思います。

まずは長方形同士から

SATによる実装の前に、もっと簡単な当たり判定の実装から見ていきましょう。長方形同士の当たり判定です。

class Rectangle {
    public float x;
    public float y;
    public float w;
    public float h;

    public Rectangle(float x, float y, float w, float h) {
        this.x = x;
        this.y = y;
        this.w = w;
        this.h = h;
    }

    public static boolean Collide(Rectangle a, Rectangle b) {
        return ((a.x <= b.x && b.x <= a.x + a.w) || (b.x <= a.x && a.x <= b.x + b.w)) &&
                ((a.y <= b.y && b.y <= a.y + a.h) || (b.y <= a.y && a.y <= b.y + b.h));
    }
}

この当たり判定では、X軸方向での長方形同士の重なりとY軸方向での長方形同士の重なりを確認し、両方とも重なっているときに当たっていると判定しています。

図にすると以下のようになります。

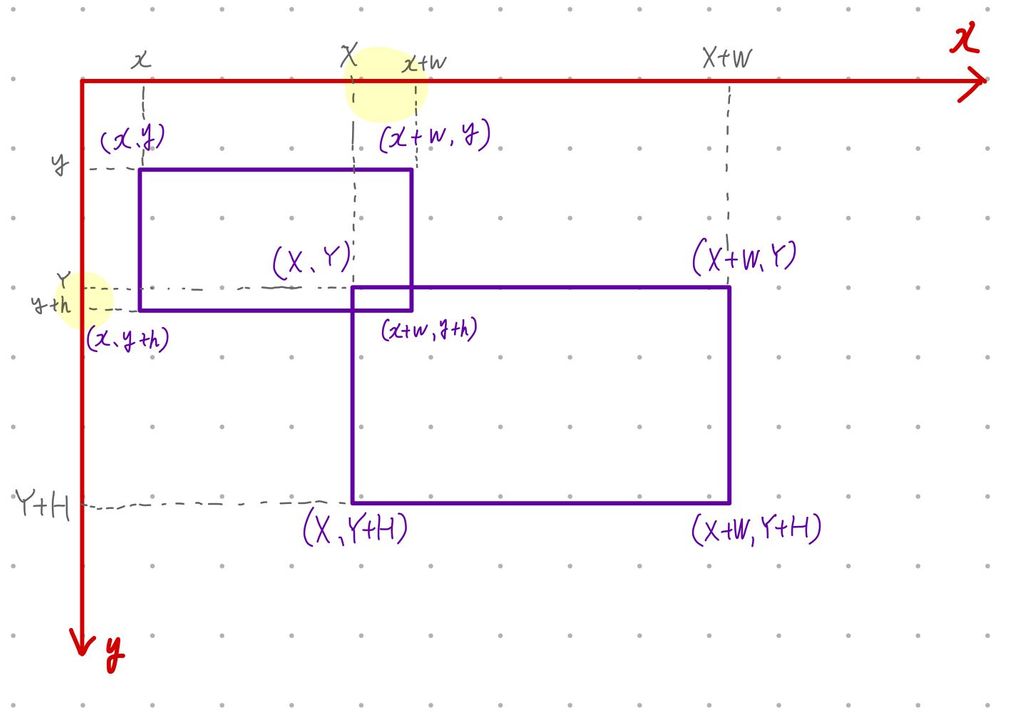
非常にシンプルな当たり判定ですが、基本的なところではSATによるものと変わりません。

SATによる多角形同士の当たり判定

説明的な

先ほど述べたように、2つの図形が重なっていないときはその間に直線を引くことができます。したがって、当たり判定では直線を引くことができるかどうかを確かめることになります。

つまり、当たり判定の実装方針は次のようになります。

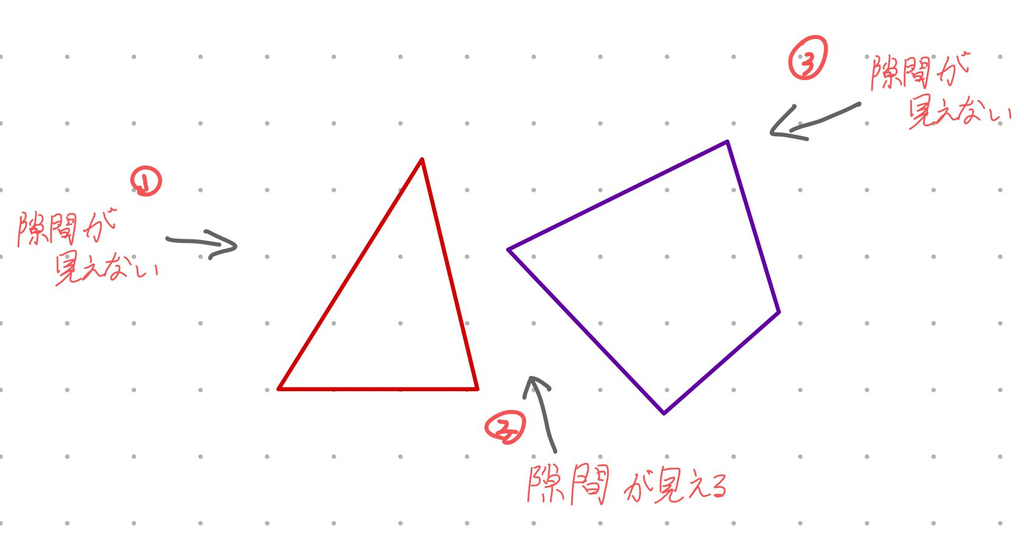
「様々な方向から図形を見て、図形同士の間に直線を引くことのできる隙間があるか確かめる」

わかりにくいな、と自分でも思ったので図に示します。この図では、②の方向から隙間が見えたため重なっていないとわかります。

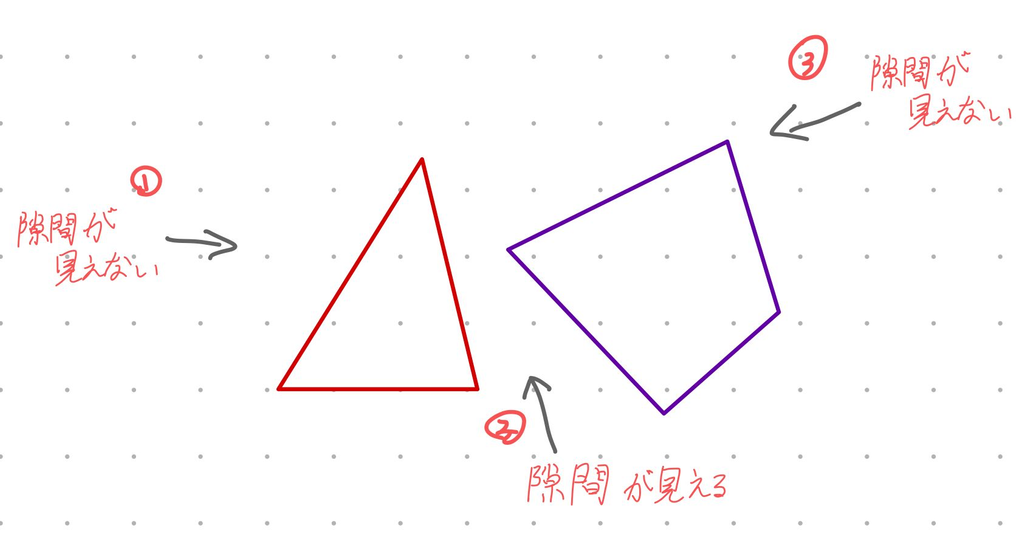
さて、様々な方向から図形を見るといっても、一体どれだけの方向から見れば隙間がないと言い切れるのでしょうか？

隙間に引かれるであろう直線について考えることで、これについての答えを得ることができます（申し訳ないですが証明などはしていません）。

隙間に引かれる直線は必ず線分と線分の間（この「間」は厳密な定義のある言葉ではないです）に引かれるので、片方の線分に並行であっても問題ありません。したがって、すべての辺に関して、並行かつ隙間を通る直線が引けるかどうかを確かめればよいのです。

隙間があるかどうかを確認するには、辺に垂直な直線に対する図形の射影が重なっているかどうかを確認します。図では、辺ABに垂直な直線でそれを行っています。

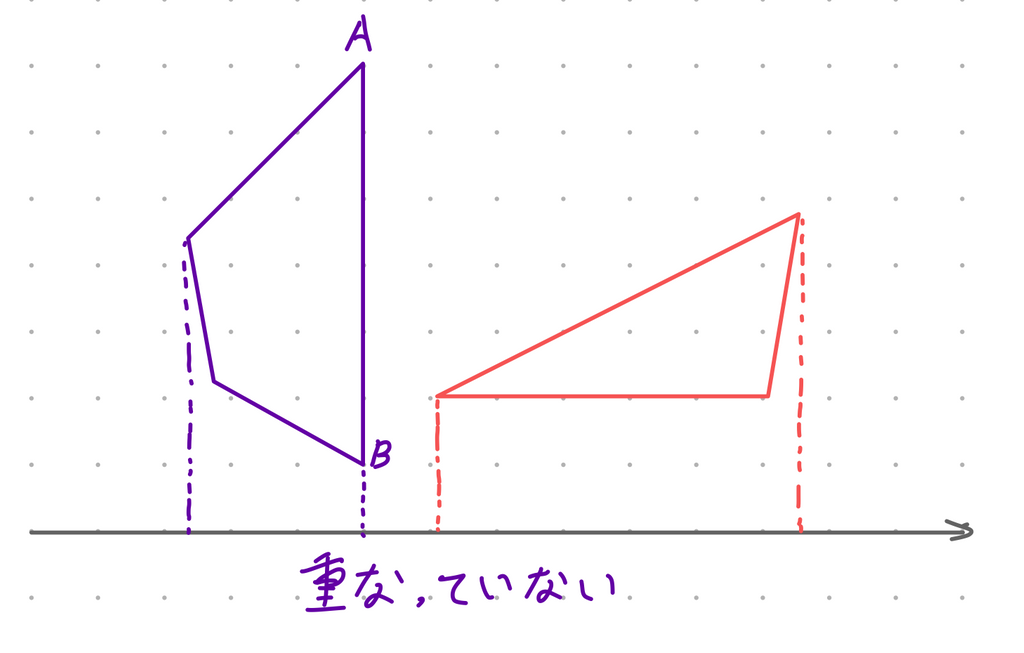
射影は二次元ベクトルの内積を用いて得ることができます。

つまり（？）、先ほどの長方形同士の当たり判定はSAT法と同じことを長方形に限定して行っていたわけです。

実装的な

説明が面倒になったので、実装について説明します。急いで書いたため見苦しいコードになっている部分もありますが、気にしないでください。

二次元ベクトル Vector2

当たり判定には二次元ベクトルの計算を必要とするので、それと必要な計算を定義してやります。特別説明が必要な部分はなさそう。内積についてはググるか、高校数学の教科書や参考書を読むとなんとなくわかると思います。

// 二次元ベクトル
class Vector2 {
    public float x; // x要素
    public float y; // y要素

    // コンストラクタ
    public Vector2(float x, float y) {
        this.x = x;
        this.y = y;
    }

    // 内積 Dot(a, b) = |a||b|cosθ
    public static float Dot(Vector2 a, Vector2 b) {
        return a.x * b.x + a.y * b.y;
    }

    // 法線ベクトル 垂直な直線のために必要
    public static Vector2 Normal(Vector2 a) {
        // 法線ベクトルは2個あるが今回の用途では片方だけでよい
        return new Vector2(a.y, a.x * -1);
    }

    // ベクトルの引き算
    public static Vector2 Minus(Vector2 a, Vector2 b) {
        return new Vector2(a.x - b.x, a.y - b.y);
    }
}

多角形 Polygon

多角形同士の当たり判定には多角形が必要であることが一般に知られているので、定義します。頂点は配列で持ち、時計回りの順に並んでいることを制約としました。試していませんが、反時計回りであっても順番の規則が統一されているなら問題ないはずです。

// 多角形
class Polygon {
    public Vector2[] vertices; // 頂点の座標 時計回りの順になっている必要がある

    // コンストラクタ
    public Polygon(Vector2[] vertices) {
        this.vertices = vertices;
    }
}

このPolygonクラスに、メソッドなどを追加して当たり判定を書いていきます。

まずはそれぞれの辺に垂直なベクトル（以降、軸と呼びます）を計算し、リストとして返す関数を作成します。頂点Bの座標から頂点Aの座標を引いて得られたベクトルABに垂直なベクトル、頂点Cの座標から頂点Bの、、、と続けて軸をリストに追加しています。

    // それぞれの辺に対して垂直なベクトルのリストを作成する
    private static ArrayList<Vector2> getAxes(Polygon a, Polygon b) {
        var axes = new ArrayList<Vector2>();

        for (var i = 0; i < a.vertices.length; i++) {
            var p1 = a.vertices[i];
            var p2 = i == a.vertices.length - 1 ? a.vertices[0] : a.vertices[i + 1];
            axes.add(Vector2.Normal(Vector2.Minus(p2, p1)));
        }

        for (var i = 0; i < b.vertices.length; i++) {
            var p1 = b.vertices[i];
            var p2 = i == b.vertices.length - 1 ? b.vertices[0] : b.vertices[i + 1];
            axes.add(Vector2.Normal(Vector2.Minus(p2, p1)));
        }
        return axes;
    }

次に必要になるのは、軸に対する射影を得るメソッドです。最初に1頂点から射影の範囲を作成し、そこからは射影が広がるたびに値を更新しています。

    // 多角形の直線に対する射影を得る
    private float[] Projection(Vector2 axis) {
        var min = Vector2.Dot(axis, vertices[0]);
        var max = min;

        for (var i = 1; i < vertices.length; i++) {
            var p = Vector2.Dot(axis, vertices[i]);
            if (p < min) {
                min = p;
            } else if (p > max) {
                max = p;
            }
        }
        return new float[]{min, max};
    }

最後に、2つのメソッドを用いて当たり判定を書きます。それぞれの軸に対しての射影を取り、それらが重なっているかどうかを確認しています。

    // 当たり判定本体
    public static boolean Collide(Polygon a, Polygon b) {
        // 軸のリスト
        var axes = getAxes(a, b);

        for (var i = 0; i < axes.size(); i++) {
            var ap = a.Projection(axes.get(i)); // 軸に対しての射影
            var bp = b.Projection(axes.get(i));

            if (!((ap[0] <= bp[0] && bp[0] <= ap[1]) || (bp[0] <= ap[0] && ap[0] <= bp[1]))) {
                return false; // 射影同士が重なっていないなら当たっていない
            }
        }
        return true; // すべての垂直なベクトルに対して射影が重なっていれば当たっている
    }

以上で、多角形同士の当たり判定が完成しました。

一応リポジトリを公開しておきます。https://github.com/FourmiSushi/SATCollisionDetection

おわりに

いかがでしたか？つい先日まで何を書くか迷っていたため、いかがでしたか記事になってしまいましたが、この記事が誰かの助けになれば幸いです。

明日はebiさんの記事です。お楽しみに。

記事候補になっていたもの

• MonoGameでゲームを作ってみた的な記事（作るのが途中で面倒になったのでやめた）（個人的に最近C#が好きになっています）
• 好きなゲームの紹介（あまりにも手抜き記事になりそうだったのでやめた）（Vaganteというゲームを紹介するつもりでした）
• 一意型について勉強して紹介する（間に合いそうになかったのでやめた）