この記事は東京工業大学デジタル創作同好会traP アドベントカレンダー2019の12/16の記事です。

こんにちは、19のxxpoxxです。いつもは競技プログラミング(AtCoder:緑)やゲームの開発、部内サービスの開発などをしています。
競プロは始める際に壁に当たることは少ないのですが、少しできるようになってきたあたり、つまり中級者になれそうな時に壁に当たることが多いと思います。僕も今めちゃくちゃ壁にぶつかっています...
この記事では、競プロ初心者や僕のような中級者になれない人がレベルアップするために覚えておくべきアルゴリズムをまとめていきます。
そもそも、競技プログラミングとはなんぞや？という人は今年の新歓ブログリレーでeiyaさんが書いた記事を読んでみましょう。

対象読者

この記事は以下の人を対象にしています。

• 競プロを始めたばかりの人
• AtCoderの100点、200点程度の問題は解けるものの300点問題から詰まってしまうような人

中級者になるためには？

なにをすればいいのでしょう。わかっていたら僕はとっくに水色になっています答えはただひとつ、問題を解くことです。過去のABCの問題を解くことで、解ける問題も増えていきます。しかし、すぐに気づくと思います。全然解けない(´；ω；｀)
競プロはただ発想力や数学力を問うものではなく、アルゴリズム力や実装力を問うものでもあるのです。つまり、なにも勉強せずにただ問題を解いたところで全ての問題が解けるようになるわけではありません。そこで、C問題やD問題を解くために必要なアルゴリズムをまとめていこうと思います！計算量などの話も少しだけ出てくるのですが、わからない方はなんか早くなるんだなと思っておいてください。 けんちょんさんの記事を読んでみてください。
なお、ソースコードの例はC++、Pythonの順に載せています。また、実行のために必要な諸々(main関数やimport、入力値など)は補ってください...

目次

• 二分探索
• 累積和
• DP

二分探索

めっちゃ有名なアルゴリズムです。

理論、考え方

以下のようなソートされた配列があったとします。

$$a[5]=[1,2,4,7,22]$$

この配列に$22$が含まれているか調べたいとき、どのようにすれば良いでしょうか。普通の人は$22$が要素に含まれるか、前から見ていくと思います。これをプログラムにすると、以下のようになります。

for(int i = 0; i < 5; i++){
    if(a[i] == 22){
        cout << "存在する" << endl;
    }
}

for i in a:
    if i == 22:
        print("存在する")

しかし、この例の場合、処理の回数は$5$回となります。今回は5個の配列なので、コンピュータで実行すればすぐに結果が返ってきますが、これが$10^{10}$個の要素を持つ配列だったらどうでしょうか...？
そのような時に登場するのが二分探索です！
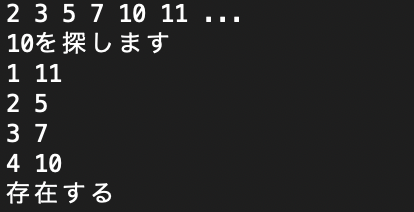
先ほどの例を用いて説明します。二分探索はその名前の通り、二つに分けて目的の要素を探していくものです。先ほどの例で$22$を二分探索で探索するには、以下のようにします。

1. 配列の真ん中の要素、つまり4を見る。
2. $22$がそれより大きいか小さいかを判断し、大きい場合は4より上の範囲、小さい場合は4より下の範囲の真ん中の要素を見る。もし$22$なら存在すると判断する。(今回の場合は大きいので[7, 22]を見てその真ん中の要素、つまり22を見る)
3. $22$がそれより大きいか小さいかを...(ry
4. 最後までとり、$22$ではなかったら存在しないと判断する。

というように真ん中で区切って大小を比較し、再び真ん中で区切って...と繰り返していき、一度も目的の要素を取らなかったら存在せず、取ったら存在するというように探索していきます。

実装

一見難しいように見えますが(真ん中の取り方とかおかしくない？と思うかもしれません)、プログラムにすると、再帰関数を用いて次のようになります。真ん中はfloor((i+j)/2)でとっていますね。

int binary_search(int i, int j){
    int m = floor((i+j)/2);
    if(i > j){
        cout << "存在しない" << endl;
        return 0;
    }else{
        if(a[m] == ans){
            cout << "存在する" << endl;
            return 0;
        }else if(a[m] > ans){
            binary_search(i, m-1);
        }else{
            binary_search(m+1, j);
        }
    }
}

def binary_search(i, j):
	m = math.floor((i+j)/2)
	if i > j:
		print("存在しない")
		return
	else:
		if a[m] == ans:
			print("存在する")
			return
		elif a[m] > ans:
			binary_search(i, m-1)
		else:
			binary_search(m+1, j)

これを用いるのは、配列にある値が含まれているのか探す場合などです。理解することができたら、二分探索を用いる問題をAtcoder Tagsから選んで解いてみましょう！

累積和

配列のある区間における要素の和を$O(1)$でとってこられるようにする、$O(N)$のアルゴリズムです。

理論、考え方

例えば以下のような配列があったとします。

$$a[10^5]=[5,4,7,12,22,\cdots ,4]$$

この配列の$a[3]$から$a[40000]$までの和が、$10^5$回のループの中で必要になったとします。
愚直に3から40000まで足していくのが愚直に求める方法ですが、これではTLEになってしまうでしょう。困りました...
ここで現れるのが累積和というアルゴリズム(考え方？)です。内容は簡単で、予め最初の要素から各要素の合計を配列に記録しておく、というものです。つまり、上の例なら次のようになります。

$$sum[10^5+1]=[0,5,9,16,28,50,\cdots ]$$

これを$O(N)$で持っておいて、$O(1)$でとってくる、ということです。先ほどの$a[3]$から$a[40000]$までの和は$sum[40001]-sum[3]$とすればよいですね！

実装

簡単です。こんな感じです。適当に$a[i-5]$から$a[i]$の和を全て出力します。

sum[0] = 0;
for(int i = 0; i < N; i++){
    sum[i+1] = sum[i] + a[i];
}
for(int i = 5; i < N; i++){
    cout << sum[i+1] - sum[i-5] << endl;
}

sum.append(0)
for i in range(N):
    sum.append(sum[i] + a[i])
for i in range(5, N):
    print(sum[i+1] - sum[i-5)

$O(N)$で処理できましたね！
累積和を用いる問題をもっと解きたいという方はAtcoder Tagsから選んで解いてみましょう！！

DP(DynamicProgramming)

漸化式(のようなもの)を立てて様々なものを求めるアルゴリズムです。
次のような問題を考えてみましょう。

価値が $v_i$ 重さが $w_i$ であるような $N$ 個の品物と、容量が $W$ のナップザックがあります。次の条件を満たすように、品物を選んでナップザックに入れます:

• 選んだ品物の価値の合計をできるだけ高くする。
• 選んだ品物の重さの総和は $W$ を超えない。

価値の合計の最大値を求めてください。

入力:１行目に２つの整数　$N$、$W$　が空白区切りで１行に与えられます。 続く $W$ 行で i 番目の品物の価値 $v_i$ と重さ $w_i$ が空白区切りで与えられます。

出力:価値の合計の最大値を１行に出力してください。

制約:

• $1\le N\le 100$
• $1\le v_i\le 1000$
• $1\le w_i\le 1000$
• $1\le W\le 10000$

この問題は、どのようにして解けばいいのでしょうか。おそらく、DPを知らないとどこから手を出せばいいのかもわからないと思います。

理論、考え方

では、実際にDPを使って解いていきましょう。
DPとは、漸化式を作ると言いましたが、これは実際には主に配列を用いて表現します。とても簡単な例を言うと、$dp[i+1]=max(dp[i]+cost[i],dp[i])$のような形です。このように式を作るには、まずなにを式にするのかが大切になります。これは問題を実際にたくさん解いて身につけていきましょう。この問題では、配列dp[$i+1$][$w$]を$i$までの重さの総和が$w$以下で最大化した価値であるとします。すると、dpの漸化式は以下のように考えることができます。
$w>=w[i]$のとき

$$dp[i+1][w]=max(dp[i][w-w[i]]+v[i],dp[i][w])$$

$w<w[i]$のとき

$$dp[i+1][w]=dp[i][w]$$

少し解説します。
まず、上の式は$i$番目まで価値を最大にとってきたときに、$i+1$番目において、品物をナップザックに入れられる状態を表しています。$w$が$w_i$よりも大きいときには、$w-w$[$i$]までの重さで価値を最大化させてきたナップザックに$w$[$i$]の重さの品物を入れて$w$までの重さで価値を最大化させた状態が作れますよね？さらに追加できるときに追加したほうが価値が大きくなるかどうかを判断するために、max関数を用いて価値を最大化させています。
同様に$w$が$w$[$i$]よりも小さいときにはナップザックに追加できないので(追加すると$i+1$番目での重さの総和が$w$を超えてしまう)、そのような場合にはそのままの価値を受け継ぎます。
ここで、漸化式を使うには初期値が必須です。DPを用いる時には忘れないようにしましょう。今回の場合は、初期値は$dp[0][0]=0$と定めることができます。そして、$N$個を使って$W$までの重さで価値の最大化を行えばいいので、求めるのは$dp[N][W]$であることがわかります。

実装

プログラムにすると、次のようになります。なお、実行できるように変数名を少し変えています。

int dp[N+1][W+1];
dp[0][0] = 0;
for(int i = 0; i < N; i++){
    for(int w = 0; w < W+1; w++){
        if(w >= c[i]){
            dp[i+1][w] = max(dp[i][w-c[i]] + p[i], dp[i][w]);
        }else{
                dp[i+1][w] = dp[i][w];
        }
    }
}
cout << dp[N][W] << endl;

dp=[[0 for i in range(W+1)] for j in range(N+1)]
for i in range(N):
    for w in range(W+1):
        if w >= c[i]:
            dp[i+1][w] = max(dp[i][w-c[i]] + p[i], dp[i][w])
        else:
            dp[i+1][w] = dp[i][w];
print(dp[N][W])

このように、$i$番目と$i+1$番目で関係性が見えてきそうな問題には、DPを使ってみましょう！実はこの問題はAOJで実際に解くことができるとても有名なナップザックDPという問題です！理解できたら解いてみましょう。また、他にもDPの問題が解きたいという方は、Atcoder Tagsから解いてみましょう。さらに、DPにはこのような基本的なものからとても難しいものまでたくさんの種類があります。†完全に理解した†方は、他のDPも勉強してみましょう！

さいごに

レベルアップするためのアルゴリズムや考え方を3つ紹介してきましたが、いかがでしたでしょうか？紹介したいアルゴリズムはもっとあるのですが、長くなりそうなので絞って紹介しました。わかりにくい点がありましたらコメントやTwitterなどで質問してください。また、自分も勉強中なので間違っている点があるかもしれません。そのような場合はコメントやTwitterで馬鹿にしてください...もっといろいろなものを知りたい、より詳しく知りたいという方は、ググってみたり、蟻本^[1]を買ってみるといいと思います。

明日、12月17日はmazreanくんの記事です。お楽しみに！